基于精确建模的横向振动工况下螺栓松动机理研究

，，，

(1.大连理工大学 机械工程学院，大连 116024;2.中国东方红卫星股份有限公司，北京 100081)

0 引言

由于连接力大、结构紧凑、便于拆卸等优点，螺纹连接结构广泛存在于各类机械结构中，是最常用的紧固手段之一。但在振动环境中工作的螺纹联接结构会出现夹紧力的持续下降甚至失效，即螺栓松动，成为重大安全隐患。因此,研究螺纹连接结构松脱现象具有重要意义。

振动工况下载荷按照其作用方向可分为4类：沿螺栓轴向的拉压力、垂直于螺栓轴向的横向力、沿螺栓轴向的扭矩以及垂直于螺栓轴向的弯矩[1]。Junker[2]于1969年最早提出，对于螺纹联接来说，动态的横向载荷比轴向载荷更能引起其松动；并提出斜坡-滑块简化模型，设计了Junker松动实验机，指出螺纹联接受横向振动作用时，其周向(拧松方向)的摩擦系数会变小，从而失去自锁功能，发生滑移并松动。内华达大学的Jiang等[3]的研究显示松动行为可以划分为两个阶段：第一阶段中，螺母与螺栓之间没有相对运动或者相对运动非常小，螺栓张紧力的下降主要是材料塑性变形及其扩展引起的；第二阶段中，伴随比较明显的螺栓旋出或者螺栓与螺母之间的相对转动，张紧力下降明显。Jiang等通过实验观测与弹塑性有限元模型分析证实：承受循环侧向载荷的螺栓的材料松动期的松动是由旋合螺纹牙底的循环塑性变形引起的。南佛罗里达大学的Pai和Hess[4]认为接触状态可分为局部滑动和完全滑动这两类，与完全滑动所需要的侧向载荷相比，累积局部滑动所需要的侧向载荷相对低得多。东京大学的Izumi等[5]在Hess的研究基础上指出，接触状态应该分为3种:没有黏着区域的完全滑动、没有稳定黏着区域的微小滑动、有稳定黏着区域的局部滑动。研究的结果还显示，只要任意接触面有稳定的黏着区域，那么螺栓就不会转动，即松动不会进行；并在侧向载荷引起的松动方面进行了理论及实验研究，并定义了可以使螺纹头部支撑面产生相对滑动的被紧固件之间的最小滑动量为临界滑动。Sanclemente等[6]的研究结果显示，在拧紧过程中，大摩擦系数会使螺栓产生更大的弹性扭转变形，在载荷施加的过程中，弹性应变能的释放会使得螺栓有较大的初始松动，但并没有分析其扭转弹性应变能究竟在何时以多快的速度释放。

本文在以上研究的基础上，通过建立精确的螺纹连接结构三维模型，采用转角法施加预紧力，并进行横向振动的瞬态分析，研究螺栓扭转变形对螺纹连接结构的松动规律。

1 螺栓连接模型横向振动仿真方法

1.1 螺纹连接结构有限元建模

研究螺纹结构在横向振动下的松动情况，不能使用螺纹轴对称模型，需考虑螺纹升角的影响。本文螺纹部分的建模主要是通过对螺纹截面的2D网格进行旋转平移来完成建模的，利用UG软件画出螺纹轴向截面曲线，结合Hypermesh网格划分软件，建立带有螺纹升角的螺纹连接结构有限元模型，如图1所示。

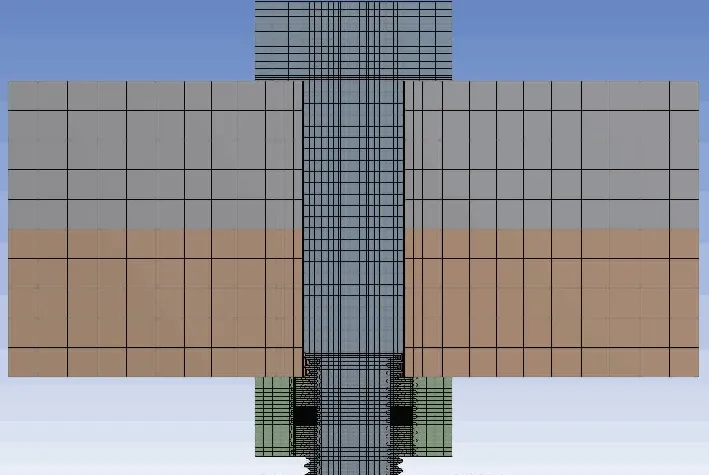
图1 螺纹精确有限元模型Fig.1 Accurate finite element model of thread

该螺纹连接结构由螺栓、螺母、上连接板、下连接板4部分组成。模型具体尺寸如下：螺栓公称直径D=10mm，螺栓公称长度l=40mm，螺纹长度b=12.5mm，螺栓头部直径Db=20mm，螺栓头部高度k=8mm，螺母高度H=8mm，螺母直径Dn=20mm，螺距p=1mm，螺纹牙型角为60°，上连接板尺寸为70mm×60mm×15mm，上下连接板尺寸相同，螺栓杆部与连接件之间孔隙为δ/2 =0.2mm。螺栓等级为8.8级高强度螺栓，弹性模量E1=206GPa，泊松比λ1=0.3，密度ρ1=7.85×103kg/m3，屈服强度λs1=640MPa；连接板材料为45#钢，弹性模量E2=210GPa，泊松比λ2=0.3，密度ρ2=7.90×103kg/m3，屈服强度λs2=355MPa。

1.2 材料属性设置和接触设置

定义材料属性Property，设置材料截面属性Section，赋予零件材料特征，本文设置了模型的塑性材料参数，考虑了材料的塑性变形。

由于在螺纹牙处划分了细致的网格，本文采用的网格单元类型为C3D8R(8节点六面体线性减缩节分单元)，单元总数为99650，节点总数为111096，使用ABAQUS/Explicit显示求解器求解[7-8]，使用面对面离散方法，在螺纹头部承压面、螺母头部承压面及上下连接板之间建立接触对，其他设置通用接触，采用Penalty contact method，设置Sliding formulation 为 Finite sliding，并设置全局摩擦系数0.15[9-10]。

1.3 分析步设置

分别设置Step-1、Step-2、Step-3这3个显示动态分析步，Step-1为转角法螺栓拧紧分析步，Step-2为撤销约束后螺栓自松弛分析步，Step-3为施加横向位移载荷分析步。分别对应仿真中的转角法施加螺栓结构预紧力、不受外力作用下自松弛、施加横向位移载荷横向激励3个阶段[11]。这样更符合螺栓结构实际工作状态，更有利于螺栓连接结构松动规律的多阶段、全过程仿真。

1.4 载荷及约束设置

本文针对仿真中的3个不同阶段，分别设置不同的载荷及约束设置。

(1)转角法施加螺栓结构预紧力阶段

在有限元仿真中，对于螺纹预紧力的施加，已有文献多数采用降温法或截面预紧力施加法，这在螺栓初始预紧力分析及静强度分析中，得到了很好的效果。但对于螺纹连接横向振动中的松动现象来说，螺纹拧紧过程中螺牙的形变与降温法或截面法施加的预紧力引起的形变始终存在差异。为更加接近螺纹连接实际工况，本文通过转角法施加螺栓预紧力。采用运动耦合约束设置，将螺母外表面与参考点RP-1耦合，在参考点RP-1上施加转角位移，并固定螺栓头部，保留连接件的轴向自由度，施加转角位移。如图2所示。

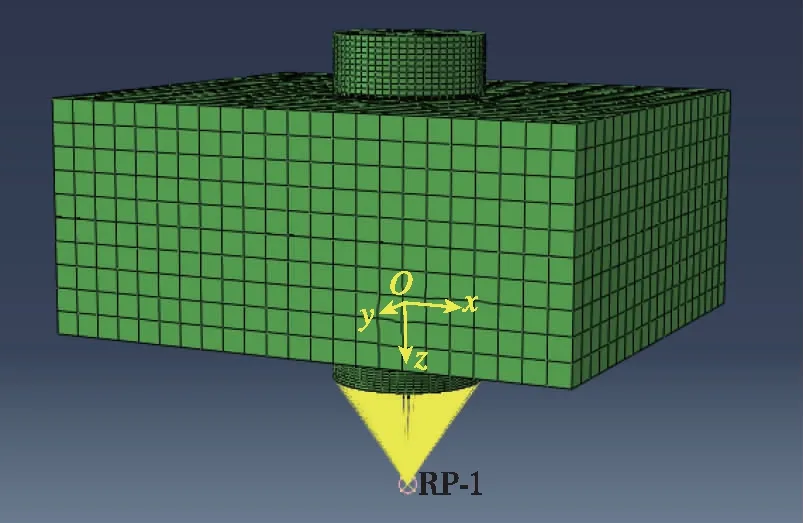
图2 转角法拧紧Fig.2 Tightening process based on the rotation angle method

(2)不受外力作用下自松弛阶段

螺纹结构拧紧后，在不受外力作用下，由于螺栓杆部扭转变形、螺纹牙底的塑性变形等原因导致预紧力下降，因此有必要在此阶段进行仿真。在此阶段，撤销了螺栓螺母上的约束与载荷，仅固定下连接板，并保留上连接板的转动自由度，进行自松弛仿真。

(3)横向位移载荷横向激励阶段如图3所示，本文施加的横向位移载荷，是根据国标GB/T 10431—2008《紧固件横向振动试验方法》[12]中规定的紧固件横向振动正弦位移载荷确定的。在自松弛阶段后，固定下连接板，将上连接板与YOZ平面平行的侧面所有节点与参考点RP-2耦合，在参考点RP-2上施加正弦位移载荷，并进行分析[13]。施加的正弦位移为：

图3 横向位移载荷施加Fig.3 Application of lateral displacement load

X=δ·sinωt

(1)

式中，δ为正弦位移载荷幅值，ω为角频率。ω与正弦位移载荷频率之间的关系为：

ω=2πf

(2)

2 拧紧阶段和自松弛阶段结果分析

本次仿真选取的螺栓等级为8.8级高强度螺栓，连接板材料为45#钢，拧紧时间为0.5s，撤销约束自松弛为0.5s，横向振动激励为5.5s。为了更清晰地反应螺栓拧紧后由于自松弛阶段的预紧力下降情况，此处将转角法拧紧阶段和不受外力作用的自松弛阶段一起分析。

2.1 转角法拧紧阶段

高强度螺栓预紧力的大小跟螺栓的材料及横截面面积有关。国内高强度螺栓的材料一般为45#钢、40B钢和40Cr钢，材料经调质处理提高螺栓机械性能。45#钢用作8.8级螺栓，40B钢和40Cr钢用作10.9级螺栓，计算公式如下[14]：

P0≤(0.5～0.6)σbAs

(3)

式中，σb为螺栓材料经热处理后的抗拉强度极限，单位为N/mm2；As为螺栓的公称应力截面面积，单位为mm2，按内螺纹小径计算。本文所用8.8级高强度螺栓材料为调质后45#钢，其抗拉强度极限约为1000N/mm2，内螺纹小径为8.376mm，由公式(3)计算得初始预紧力F0≤0.6σbAs=33.044kN。对于受交变外载作用的螺纹联接结构施加的预紧力要比受静态外载作用的螺栓大些。

本文在螺母外表面节点施加转角位移，此转角位移以螺母与下连接件贴合但没有接触力为零点，拧紧角度为40°，拧紧时间为0.5s，自松弛时间为0.5s，提取两连接件之间的夹紧力作为预紧力，所得预紧力为32.924kN。因本文所用模型为承受交变载荷高强度螺栓，此预紧力在接受范围内。连接件结合面预紧力上升曲线如图4所示。

图4 连接件结合面预紧力上升曲线Fig.4 Preload increase curve of connecting surface of connecting piece

根据螺纹连接的相关理论[15]，螺栓连接结构在拧紧时，螺纹牙轴向载荷分布并不均匀，从靠近连接板到螺母顶端的螺纹牙所受载荷呈单调递减趋势。如图5所示，本文以B1表示靠近连接板的第一圈螺纹牙，后几圈螺纹牙依次以序号表示，下文相同。可以看出，转角法拧紧螺栓后其承受轴向力最大，占预紧力的23.72%，前4圈螺牙占预紧力的68.9%，与理论相符合。

图5 自松弛后各螺纹牙受力饼状图Fig.5 Pie chart of each thread after self-relaxation

2.2 转角法拧紧后自松弛阶段

由于螺母上表面和下表面、内表面和外表相对转角很小，在后续的分析中，本文将螺母作为刚体分析，只把单独的螺栓作为分析对象。

由图6、图7所示，取螺母外圆面的轴向转动角度和第一圈螺纹轴向转动角度比较，可知在螺栓结构不受外力作用下的自松弛阶段，螺母转角虽有所回转，但与螺栓螺纹回转角度相差无几。可以认为在此阶段，螺栓由于在拧紧之后螺栓杆部存在扭转变形，导致螺栓螺纹和螺母螺纹共同回转。

图6 拧紧过程中螺母转角变化Fig.6 Change of screw angle of nut during tightening

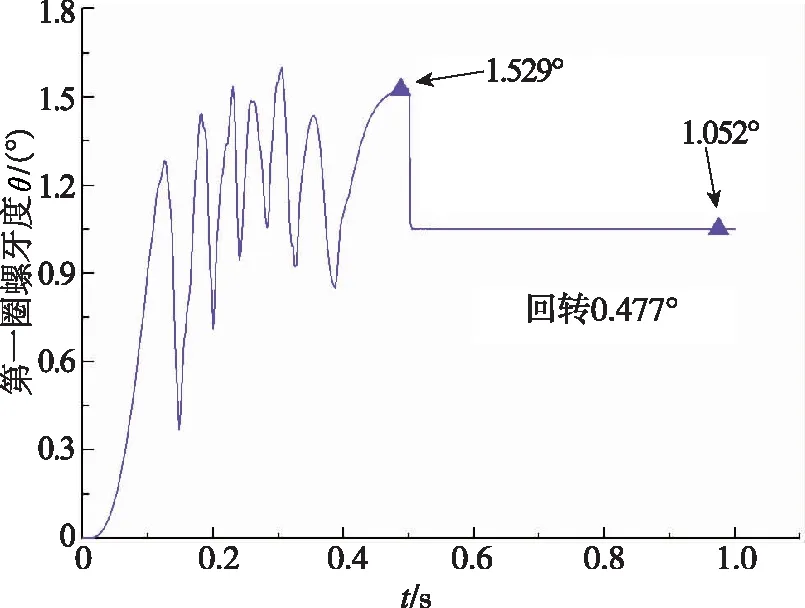
图7 拧紧过程中第一圈螺牙转角变化Fig.7 Change of screw angle of the first ring during tightening

如图6～图7所示，在自松弛阶段螺纹牙底仍然发生了塑性变形，本文认为不受外力作用的自松弛阶段预紧力的下降，主要是螺纹牙底材料蠕变效应，产生塑性变形引起的。

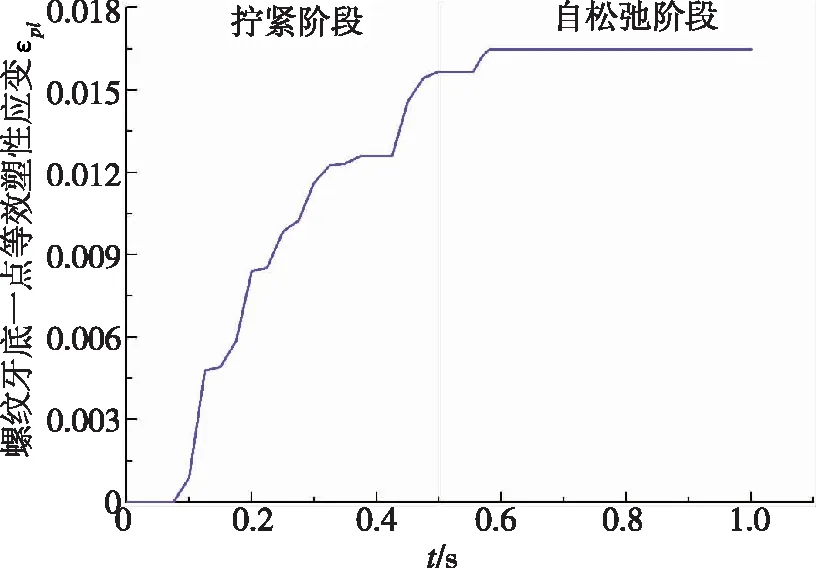
图8 螺纹牙底一点的等效塑性应变Fig.8 Equivalent plastic strain of a point at the root of a thread

3 横向位移载荷激励阶段结果分析

3.1 横向振动初期

如图9所示，根据国标GB/T 10431—2008《紧固件横向振动试验方法》中关于紧固件横向振动正弦位移载荷的相关规定[12]，本文转角法拧紧40°并自松弛后，在上连接件与YOZ平面平行的侧面所有节点施加频率为10Hz，振幅为0.2mm的正弦位移载荷X=0.2·sin(62.8t)，振动时间为5.5s，进行横向振动仿真，所得预紧力变化如图10～图11所示。

图9 横向振动位移Fig.9 Transverse vibration displacement

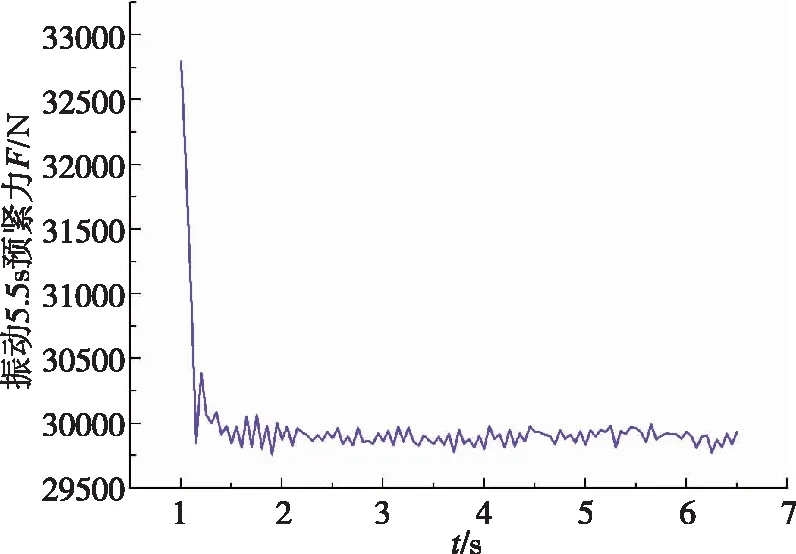
图10 预紧力变化曲线Fig.10 Preload change curve

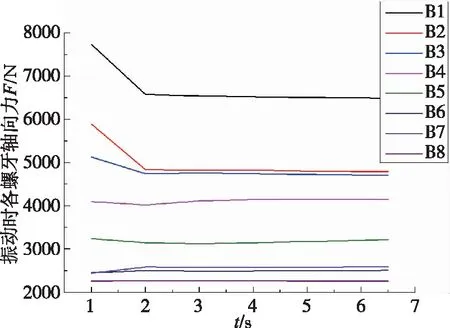
图11 各个螺纹牙轴向力变化曲线Fig.11 Axial force change curve of each thread

由图10～图11可知，螺栓连接结构受到横向位移载荷作用时，在横向振动前几个周期，预紧力有较为明显的下降，在2s时预紧力基本保持不变，进入稳定期。且连接件之间预紧力的下降，主要是前3圈螺纹牙轴向力的减小造成的。

图12 振动过程中螺纹牙底一点的等效塑性应变Fig.12 Equivalent plastic strain at one point of the thread bottom during vibration

如图12所示，提取振动过程中螺纹牙底一点的等效塑性应变，发现螺纹牙底材料在振动过程中持续发生塑性变形。本文认为横向振动前期，连接件之间预紧力的下降，也主要是螺纹牙底产生塑性变形引起的。

为进一步探究螺栓松动情况，提取振动过程中螺母和螺栓各部分的转角变化，如图12～图14所示。

图13 振动过程中螺母转角变化Fig.13 Changes in nut rotation angle during vibration

图14 振动过程中螺栓各部分转角变化Fig.14 Change of rotation angle of various parts of bolt during vibration

由图13～图14可以发现，振动过程中的前几个周期，同一坐标系下，螺母回转角度和第一圈螺纹回转角度基本相同，和最后一圈螺纹回转角度略有差别，而螺栓头部则向相反的方向转过了一定角度，螺栓杆中部一截面转过一定角度后基本保持不变。因此，本文认为在横向位移载荷作用初期，螺纹之间产生非常小的相对滑动，由于拧紧后螺栓杆部存在扭转变形，导致螺栓螺纹和螺母螺纹共同回转，螺栓头部则向相反的方向转动。此后，螺纹之间才会发生明显的相对滑动，螺母相对螺栓产生回转，造成预紧力下降。

3.2 螺栓扭转变形回弹

那究竟是什么时刻螺母和螺栓之间才开始明显的相对回转呢？为了进一步探究螺栓松动情况，本文以螺栓作为研究对象的基础上，将螺栓沿着轴线方向的扭矩作为研究对象，分析螺栓振动过程中弹性扭转回弹情况。

螺栓头部和螺纹处的轴向扭矩CMT3，均可分为因接触切向力产生的接触切向扭矩CMN3和因摩擦力产生的摩擦扭矩CMS3。螺栓连接结构受力时，因螺纹处为非平面(螺旋面)，轴向扭矩CMT3等于CMN3与CMS3两者之和；因螺栓头部为平面，则受力时螺栓头部接触切向力扭矩CMN3近似为0，因此摩擦扭矩CMS3等于总的轴向扭矩CMT3。如图15所示，为了直观地查看螺栓轴向扭矩情况，将螺栓头部轴向扭矩CMT3、螺纹处CMT3、CMN3、CMS3作图分析。

图15 螺栓各部分的轴向扭矩Fig.15 Axial torque of each part of bolt

如图15所示，对于单独的螺栓来说，在拧紧的最终阶段，也就是振动的开始时刻(对应图中1s时刻)，螺纹处的轴向扭矩CMT3(CMN3+CMS3)与螺栓头部的扭矩CMT3(CMS3)大小相等，方向相反。

本文认为，接触切向力产生的轴向扭矩CMN3和摩擦力产生的轴向扭矩CMS3，均可以看作由两种原因造成的。一种原因是螺母随螺旋线上升产生的预紧力引起的，另一种原因是螺栓扭转变形产生的，图15中的CMN3和CMS3是两种原因的矢量叠加结果。CMN3和CMS3两者的变化，不仅反映螺母与螺栓之间相对转角的变化，还反映螺栓扭转变形的变化。本文以图16中所示坐标系进行分析。

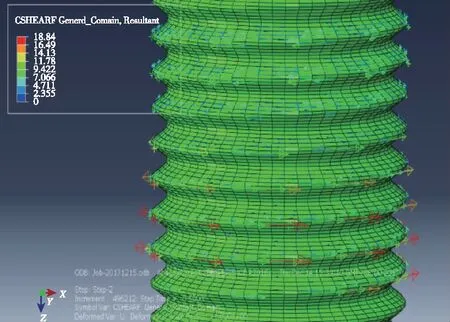
图16 拧紧后接触切向力分布Fig.16 Contact tangential force distribution after tightening

在此坐标系下，在拧紧后不受外力情况下，对螺栓螺纹来说，接触切向力产生的扭矩CMN3为负值。图16为本文提取螺栓螺纹处接触切向力示意图。由于使用的螺纹为右旋螺纹，发现前几圈螺纹受到的接触切向力主要是沿螺纹螺旋线向下的，这主要是预紧力作用引起。按右手螺旋法则，产生的扭矩为正值；而后几圈螺纹接触切向力是沿着螺旋线向上的，这主要是由螺栓轴向扭转变形回弹引起，产生的扭矩为负值。在振动开始时刻总的CMN3为负值，说明在拧紧后螺栓轴向扭转变形引起的接触切向力矩大于预紧力作用下的接触切向力矩，说明由于螺栓扭转变形产生的接触切向力扭矩起主导作用。

在此坐标系下，摩擦力产生的扭矩CMS3也为负值。由于螺母回转导致预紧力下降引起的摩擦扭矩为正值，而由于螺栓轴向扭转变形回弹产生的摩擦扭矩为负值，在拧紧结束后CMS3为负值，说明在螺栓扭转变形产生的摩擦扭矩大于由于螺母回转产生的摩擦扭矩，此时CMS3主要克服螺栓的扭转引起的回弹趋势。

在受到横向外力作用时，由于螺纹牙底材料塑性变形，螺母微量回转等因素导致预紧力减小。另外，由于螺栓头部和连接件之间发生相对滑动，螺栓头部接触由静摩擦变为动摩擦，导致螺栓头部轴向扭矩减小。由于拧紧后螺栓杆部存在扭转变形，螺栓头部轴向扭矩的减小导致螺栓头部随之转过一定角度，扭转变形产生回弹。预紧力的减小和螺栓扭转变形回弹，共同引起CMN3和CMS3变化。

由图15可以看出，由于预紧力减小和螺栓扭转变形回弹，对接触切向力产生的扭矩CMN3影响较小，CMN3在振动过程中基本保持稳定。这是因为预紧力减小和螺栓扭转变形回弹导致CMN3的减小，在矢量上相互抵消。这也表明CMN3反映着螺栓螺纹与螺母螺纹之间相对位置的变化。CMN3不变，表明横向振动初期，螺栓螺母之间的相对位置(相对转角)并没有发生明显变化，螺栓与螺母之间不产生明显滑动。

而对于摩擦力产生扭矩CMS3影响较大。从图15可以看出，CMS3在横向振动的初期，可以说首个周期，即变为0，表明此时由于螺栓扭转回弹和预紧力下降引起的轴向摩擦扭矩大小相等，方向相反，此刻(A点)螺纹处轴向扭矩只存在由于接触切向力产生的轴向扭矩CMN3。此后，螺栓扭转变形逐渐减小，预紧力引起的摩擦扭矩逐渐增大，当增大到和接触切向力扭矩CMN3相同绝对值时，螺栓头部扭矩为0(B点)。在此过程中，可以认为螺母与螺栓不发生相对转动，且螺栓头部扭矩为0的时刻(B点)表明螺栓扭转变形释放完成。当预紧力下降引起的摩擦扭矩CMS3大于接触切向力产生扭矩CMN3的绝对值时，螺母开始回转，开始产生由于螺母回转造成的预紧力的下降。

由图14中提取螺栓中部一截面轴向转角变化，可以发现当螺栓扭转回弹和预紧力下降引起的轴向摩擦扭矩大小相等，方向相反时(A点)，轴向扭转角变化最大，表明横向振动使拧紧后的螺栓杆部扭转变形回弹最大，螺栓扭转变形能释放最快。螺栓头部扭矩为0的时刻(B点)，螺栓杆部轴向扭转角基本不发生变化，表明螺栓扭转变形能释放基本完成。以此，B点此刻可以作为判别螺栓扭转变形能释放速度的节点，用以区分螺栓松动的不同阶段。但仿真达到B点的时间要长一些，计算成本较高。

综上所述，当螺栓连接结构受到横向位移载荷时，由于螺栓头部或螺母面与连接件之间发生相对滑动，导致螺栓扭转变形回弹。在螺栓扭转变形能完全释放之前(B点之前)，螺纹之间产生非常小的相对滑动，相对滑移不明显，宏观上更多的则是表现为螺栓螺纹与螺母的共同回转。但是螺栓扭转变形并不能直接导致预紧力的下降。B点之前，预紧力的下降主要是螺纹连接结构受到外力作用导致螺纹牙底塑性变形造成的；在这之后，螺母相对于螺栓才发生回转，导致预紧力的进一步下降。

4 螺栓松动实验

4.1 螺栓横向振动实验台

为验证仿真的可行性，设计了螺栓松动实验台。螺栓松动实验台由电机驱动，电机轴通过凸轮轴连接外部结构，凸轮偏心0.2mm，电机的转动带动凸轮轴运动，产生横向的正弦位移激励，与仿真相符。横向位移的测量由电涡流传感器完成，预紧力由压力传感器测量，中间增加了力传感器测量横向力的变化。数据采集由NI采集系统完成。实验台结构见图17，实验台实物见图18。

1-底座(下连接件)；2-压力传感器； 3-电涡流传感器；4-电涡流传感器支撑座 ；5-上连接件；6-固定板；7-支撑座；8-横向力传感器；9-弹性体；10-支撑座轴承；11-伺服电机；12-偏心凸轮；13-曲柄滑块；14-固定端盖；15-曲柄机构导程块；16-力传感器前端连接块；17-力传感器后端连接块；18-地脚螺栓；19-水平台图17 螺栓松动实验台结构Fig.17 Bolt loosening test bench structure

图18 螺栓松动实验台实物图Fig.18 Physical map of bolt loosening test

4.2 具体实验方法

实验台横向载荷的加载为一个对心曲柄滑块机构，三相异步电机由变频器控制转速，三相异步电机的转动为实验台提供横向载荷。将压力传感器接在PXIe-4330输入模块的转接板上，PXIe-4330输入的信号通过PXIe-1082采集系统采集，显示为力信号。由S型柱式压力传感器采集横向力载荷信号，电涡流位移传感器采集横向位移载荷信号，垫片式压力传感器采集螺栓预紧力的变化，通过预紧力的变化判断螺栓的松脱。

4.3 螺栓横向振动实验与仿真结果对比

本试验采用的螺栓以及上、下连接板的材料属性均与前文仿真中模型材料属性相同。只是由于螺母和连接板之间存在压力传感器，螺栓的公称长度l变为70mm，螺栓其他尺寸和上、下连接板尺寸均与模型相同。在螺栓与连接件之间单边孔径间隙为0.2mm的情况下，控制横向外载频率和振幅分别为10Hz和0.2mm，使用3组不同的起始预紧力12076.0N、16796.1N和25647.3N，进行螺栓松动试验，每组试验结束后更换一组螺栓螺母，横向振动时间均在10min以上。同时，松动仿真中也以三组不同的起始预紧力12516.7N、16080.1N、24945.3N进行仿真，松动仿真中以相同条件仿真5.5s，提取试验结果的前5.5s原始数据，将试验数据与仿真数据导入到Origin软件中进行非线性拟合，通过拟合曲线中预紧力的下降情况，进行试验结果与仿真结果的对比分析，以验证仿真方法的可行性。试验数据和仿真数据拟合结果如图19～图20所示。

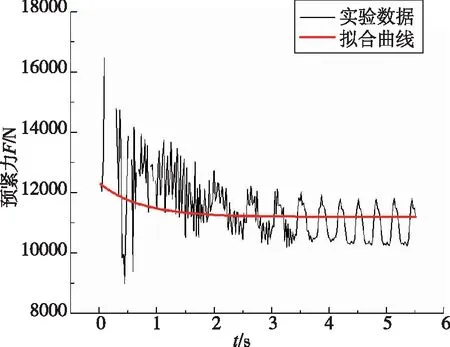
(a)起始预紧力12076.0N

(b)起始预紧力16796.1N

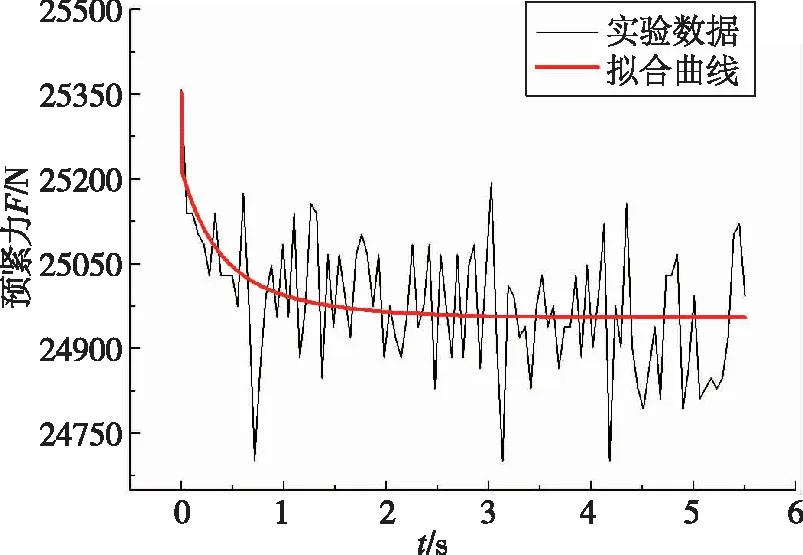
(c)起始预紧力25647.3N图19 试验数据拟合Fig.19 Test data fitting

(b)起始预紧力16080.1N

(c)起始预紧力24945.3N图20 仿真数据拟合Fig.20 Simulation data fitting

为定量对比实验和仿真误差，本文中以F0为起始预紧力，F5.5为振动时间5.5s后的终值预紧力，预紧力的下降值为ΔF=F0-F5.5，实验结果和仿真结果误差百分比为Δ，其表达式为：

(4)

本文将拟合曲线的计算结果汇总于表1。

表1 仿真结果与实验结果对比Tab. 1 Comparison between simulation results and experimental results

从表1可以看出，在实验和仿真起始预紧力有所差别的情况下，3组不同起始预紧力下的仿真拟合数据和实验拟合数据误差均在20%左右。

本文分析造成仿真结果与实验结果误差的原因:

1)传动机构间隙导致。本文所施加的横向位移载荷，是通过电机带动的传动机构作用在上连接件上，由于存在加工误差、装配误差以及零件磨损，传动机构始终存在横向间隙；而仿真中载荷施加准确无误差。

2)摩擦系数和材料塑性参数设置导致。仿真中所用模型的螺栓和连接件虽然与实验中所用材料相同，但实际材料的表面形貌特征无法具体呈现。

3)传感器误差导致。试验中压力传感器由于受到外界干扰和自身灵敏度造成误差，导致试验数据波动较大。

综上所述，仿真结果和实验结果基本吻合，若实验条件与仿真条件更为接近的话，结果相似度会更高。

5 结论

1)本文所用的转角法拧紧螺栓并施加横向位移载荷，进行的螺栓松动仿真分析结果与实验结果基本吻合。

2)螺栓结构拧紧后的自松弛阶段，螺母螺纹和螺栓螺纹相对滑动很小，此时预紧力的下降主要是由螺纹牙底材料塑性变形引起的。

3)螺栓结构在拧紧时导致螺栓杆部扭转变形，横向振动前期，螺栓连接结构支撑面之间首先发生相对滑动，导致螺栓扭转变形回弹。但是扭转变形回弹对预紧力的下降并没有直接影响。

4)提取了螺栓杆部扭转变形完全回弹的节点(B点)。在B点之前，螺纹相对滑动很小，宏观上更多地表现为螺母螺纹与螺栓螺纹共同回转，此阶段预紧力的下降，主要是单次大循环载荷导致螺纹牙底塑性变形和材料的棘轮效应引起的；B点之后，螺母开始相对于螺栓回转，由螺母回转造成预紧力的下降。