振动工况下的双螺母结构防松性能研究

， ，，

(1.北京理工大学机械与车辆学院,北京 1000812.中国航天标准化与产品保证研究院,北京 100071)

0 引言

螺栓连接是一种典型的紧固连接方式，具有拆装方便、造价低廉、互换性强、可大批量生产等优点，因此在机械产品中应用广泛[1]。在机械产品服役的过程中，螺栓连接很容易受到振动、冲击、交变温度载荷等复杂环境的影响而发生松动失效，螺栓松动将显著降低机械产品可靠性，甚至导致严重的安全事故。为了防止螺栓松动，提高螺栓连接和机械产品可靠性，工程中制定了很多的防松措施，其中双螺母连接便是一种广泛使用的典型防松措施。

许多学者对双螺母的防松效果和工作原理进行了大量的研究。杨林[2]在螺纹紧固件的振动实验中发现，双螺母结构可以产生较好的防松效果；余钦义[3]讨论了双螺母的两种拧紧方式，即上螺母顺向旋紧法和下螺母逆向旋紧法，并对这两种方式进行了受力分析；龚必强[4]对汽车板簧U形螺栓的双螺母连接结构展开研究，发现为保证连接可靠性，可根据汽车板簧结构的不同，对上下螺母拧紧力矩值做出合理调整；景秀并[5]设计实验研究上下螺母拧紧力矩与防松性能的关系，认为上螺母拧紧力矩的大小对于双螺母连接的防松性能起着关键作用；马涛[6]对双螺母结构的连接强度进行校核；鲁绪芝等[7]、金玉萍等[8]最早开始用“力—变形图”得到了双螺母连接结构在拧紧过程中的受力、变形、刚度等变化关系，为螺栓连接采用双螺母时的强度计算和防松提供理论依据；刘东亚等[9]则利用“力—变形图”得到了起防松作用时，上螺母拧紧力矩值的定量表达式；吴广益[10]、李宏天等[11]在此基础上对薄厚双螺母的合理使用做出说明。

随着计算机技术不断进步，有限元仿真为研究双螺母的防松机理提供了新的工具及方法。苑雪涛等[12]通过理论计算和有限元验证，得出上螺母拧紧结束时对螺栓产生的轴向力需达到下螺母拧紧结束时对螺栓产生的轴向力1倍以上才会起到防松效果的结论；日本东京大学的Izumi等[13]建立了双螺母结构的有限元模型，并对双螺母的防松性能进行了研究，结果表明上下螺母的轴向力分配比例是影响双螺母防松性能的主要因素。

在Izumi研究的基础上，本文采用更为细化的有限元模型对双螺母的拧紧过程以及更多振动周期的松动过程进行了观测，并采用实验对仿真结果进行了验证，系统揭示了双螺母在拧紧过程中各轴向力的变化关系以及上下螺母轴向力分配情况对螺栓防松性能的影响规律，为双螺母的拧紧工艺优化提供更为具体的参考依据。

1 双螺母拧紧过程受力分析

双螺母的拧紧方法通常有两种，即下螺母逆向旋紧法和上螺母顺向旋紧法[3]。其中，上螺母顺向拧紧法的操作更加简单方便，应用广泛，因此针对该拧紧方法进行后续研究。上螺母顺向拧紧的过程包括：1)以扭矩M1拧紧下螺母，2)固定下螺母的同时以扭矩M2拧紧上螺母，具体如图1所示。

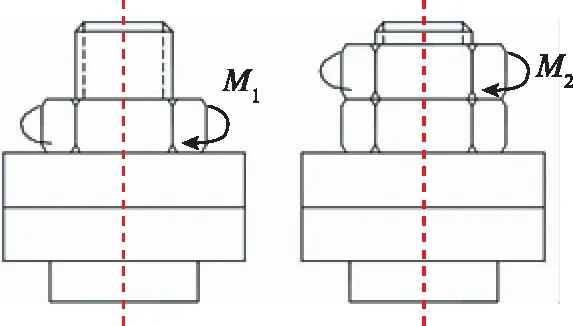
图1 双螺母拧紧方式—上螺母顺向拧紧法Fig.1 Clockwise tightening method of upper nut

下面具体分析整个拧紧过程中螺栓轴向受力的变化过程。如图2所示，以截面A、B、C、D把螺栓划分为不同的区域。由于螺纹连接的拧紧效果，AB段的材料被拉伸，从而产生了轴向预紧力。在AB区间内，任意横截面上的轴向应力并非严格地均匀分布，但应力的积分即为螺栓产生的轴向预紧力，设其为Fr。

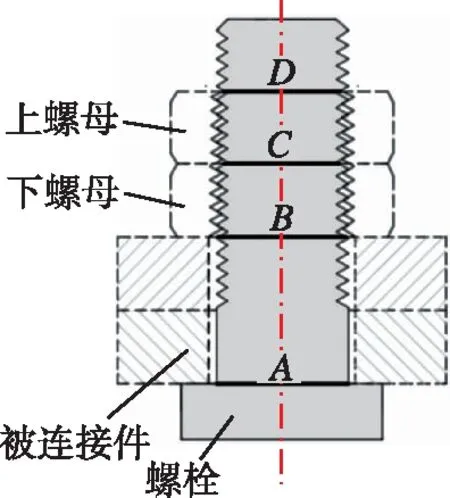
图2 螺栓受力等效区间Fig.2 Equivalent section of bolt axial force

在拧紧下螺母的过程中，如图3所示，下螺母螺纹的上表面与螺栓螺纹下表面接触，从而产生接触应力，螺栓在BC段所受接触应力的轴向分量为f1(方向向上)，在螺纹区域积分而形成轴向合力F1，

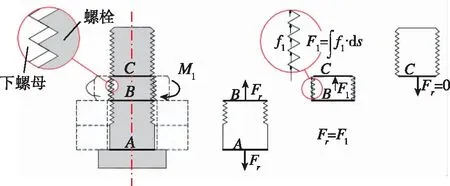
图3 拧紧下螺母时螺纹连接轴向受力分析示意图Fig.3 Bolt’s axial force analysis when the lower nut is tightened

(1)

F1为下螺母对螺栓产生的轴向力，此时螺栓轴向预紧力Fr=F1。

在拧紧上螺母的第1阶段，如图4(a)所示，上螺母螺纹的上表面与螺栓螺纹的下表面接触从而产生接触应力，螺栓在CD段所受接触应力的轴向分量为f2(方向向上)，在螺纹区域积分而形成轴向合力F2，

(2)

F2为上螺母对螺栓产生的轴向力。与此同时，下螺母螺纹上表面逐渐与螺栓螺纹下表面分离，但F1方向并没有变化，仍然向上，此时Fr=F1+F2；当下螺母螺纹上表面与螺栓螺纹下表面完全分离时，如图4(b)所示，F1=0，此时Fr=F2。

继续拧紧上螺母到第2阶段后，如图4(c)所示，下螺母的螺纹下表面与螺栓螺纹上表面产生接触，F1方向发生变化(方向向下)，此时Fr=F2-F1。此阶段的双螺母连接状态被称为完全预紧状态，当双螺母连接结构达到完全预紧状态后可以起到很好的防松效果。

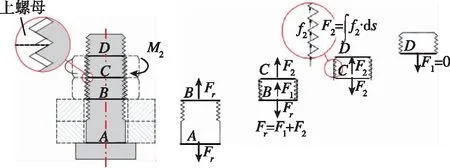
(a) 拧紧上螺母的第1阶段的受力分析

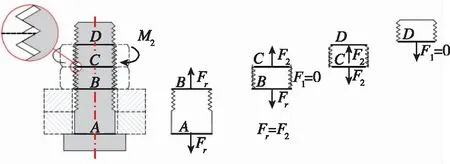
(b) 拧紧上螺母的第1和第2阶段过渡状态的受力分析

(c)拧紧上螺母的第2阶段的受力分析图4 拧紧上螺母不同阶段时螺纹连接轴向受力分析示意图Fig.4 Stages of bolt’s axial force analysis when the upper nut is tightened

2 有限元模型

本文采用有限元模型模拟双螺母拧紧及横向振动条件下轴向紧固力的衰退过程[14]。具体的模型如图5所示。该模型由上螺母①、下螺母②、活动板③以及螺栓④这4部分组成。为了保证计算精度，在上下螺母与螺栓之间、下螺母与活动板之间的接触区域进行了局部网格密化。模型的相关尺寸如下：螺栓螺母螺纹规格为M10，螺距p=1.5mm，螺母外径Dn=7.85mm，螺母高度Hn=7.5mm，螺栓头部外径Dbh=7.85mm，螺栓头部高度Hbh=6mm，螺栓总长度Lb=39mm，活动板内径Dm1=5.6mm，活动板外径Dm2=14.6mm，活动板高度Hm=9mm。双螺连接结构所有模型材料参数为：弹性模量E=206GPa，泊松比ν=0.3。有限元建模过程中的网格划分、单元定义、材料定义、接触对定义均在Hypermesh 13.0中完成，约束定义、上下螺母轴向力的施加以及横向位移的施加均在ANSYS 16.0中完成。

图5 双螺母连接结构有限元模型示意图Fig.5 FEM of double nut connection structure

根据载荷—形变特性，选用面接触单元用于建立计算分析三维接触问题的接触界面模型，选择TARGE170单元为目标面单元，CONTA173单元为接触面单元。定义的接触包括：1)上螺母与螺栓之间的接触对；2)下螺母与螺栓之间的接触对；3)上下螺母之间的接触对；4)下螺母与活动板之间的接触对。摩擦系数μ=0.15。为了提高计算效率，下螺母的拧紧过程被简化，通过在螺杆中部施加PRETS179预紧力单元而直接产生轴向力，下螺母的初始预紧力设定为10kN。而上螺母的拧紧过程则是通过MPC184单元在顶端施加扭矩来实现，如图6所示。

在模拟横向振动的过程中，在活动板侧施加周期性横向位移，横向位移取0.1mm，活动板下表面施加y、z方向约束，螺栓头部施加x、y、z方向全约束。

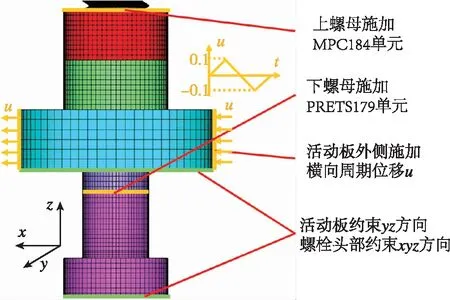
图6 有限元模型边界条件示意图Fig.6 Boundary condition setting of FEM

3 双螺母拧紧过程中各轴向力变化关系

为了更好地理解各轴向力在双螺母拧紧过程中的变化关系，利用前述的有限元模型计算F1、F2、Fr在拧紧过程中的力变化规律，并结合前述的受力分析，最终得到如图7所示的结果。需要说明的是，这里用向量F1来表示螺栓所受到下螺母的轴向力，F1的大小为F1，规定下螺母拧紧过程及上螺母拧紧第1阶段的F1为正(方向向上)，第2阶段的F1为负(方向向下)。首先由前述的受力分析可知，拧紧下螺母时(对应图3所示受力过程)，Fr随着F1的增加而增加，且有Fr=F1，因此在图7所示的下螺母拧紧阶段，F1和Fr的变化曲线重合(此部分曲线非有限元仿真得到)。下螺母拧紧结束时，设下螺母对螺栓产生的轴向力F1=F1_t。拧紧上螺母时(对应图4所示受力过程)，随着F2的增大，F1的大小及方向将会发生改变，有限元计算结果表明，Fr会缓慢增大(未超过F1_t的20%)。上螺母拧紧结束时，设上螺母对螺栓产生的轴向力F2=F2_t。

分析拧紧过程中的螺栓螺纹表面与螺母螺纹表面的接触状态，当未达到完全预紧状态时，上螺母的螺纹上表面与螺栓的螺纹下表面进行接触，而下螺母同样是其螺纹上表面与螺栓的螺纹下表面进行接触，如图8所示。当达到完全预紧状态时，上螺母的螺纹上表面与螺栓的螺纹下表面进行接触，而下螺母则是其螺纹下表面与螺栓的螺纹上表面进行接触，如图9所示。

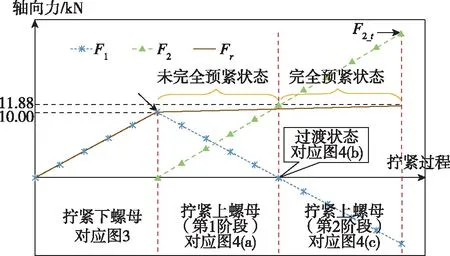
图7 拧紧过程各轴向力变化关系图Fig.7 Variation of axial force in tightening process

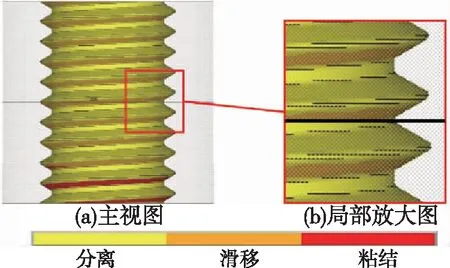
图8 未达到完全预紧状态时螺栓螺纹表面的接触状态Fig.8 Contact state of bolt thread surface when it doesn’t reach complete locking state

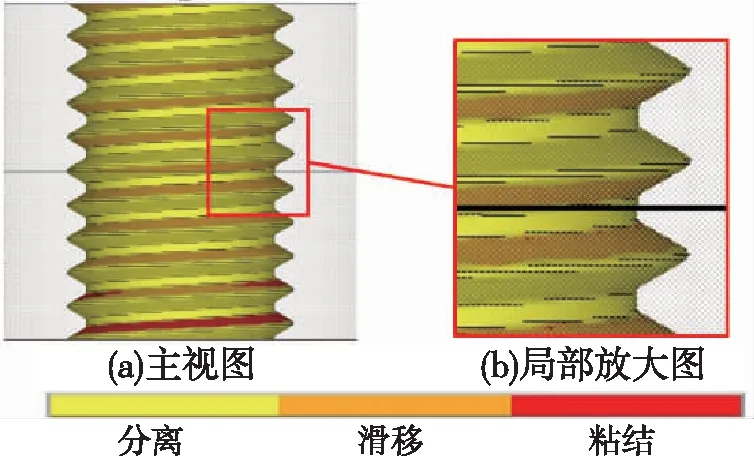
图9 达到完全预紧状态时螺栓螺纹表面的接触状态Fig.9 Contact state of bolt thread surface when it reaches complete locking state

为方便后续内容的介绍，需明确定义：

轴向预紧力：即为Fr，是指在上下螺母拧紧过程中螺栓AB段所受的轴向力，它并非定值，在下螺母和上螺母拧紧过程中，轴向预紧力会逐渐增大，拧紧结束时轴向预紧力达到其最终大小。

轴向紧固力：是指在振动过程中螺栓AB段所受的轴向力。轴向预紧力和轴向紧固力均为AB段所受的轴向力，区别在于前者是针对拧紧过程的定义，有“预先紧固”的含义，而后者是针对使用过程的定义。轴向紧固力也非定值，其初始值即为轴向预紧力的最终大小，但在使用过程中，轴向紧固力会逐渐减小。采用横向振动实验能够观测到轴向紧固力随振动周期的增加而减小的过程，其衰减速率的大小能够反映出螺栓连接结构防松性能的好坏。

轴向力分配比：F2_t与F1_t的比值称为轴向力分配比。

4 轴向力分配比对双螺母连接防松性能的影响

为了研究不同的轴向力分配比对双螺母连接防松性能的影响，本文利用前述的有限元模型，并基于如表1所示拧紧条件进行了11组仿真计算。设拧紧下螺母后F1的大小为10kN，即F1_t=10kN，而后拧紧上螺母，随着F2的增大，F1会逐渐变化，F1被控制在-10kN～10kN之间，上螺母拧紧结束时，F1、F2_t、螺栓AB段受到的轴向预紧力Fr以及轴向力分配比的大小均在表1中给出。

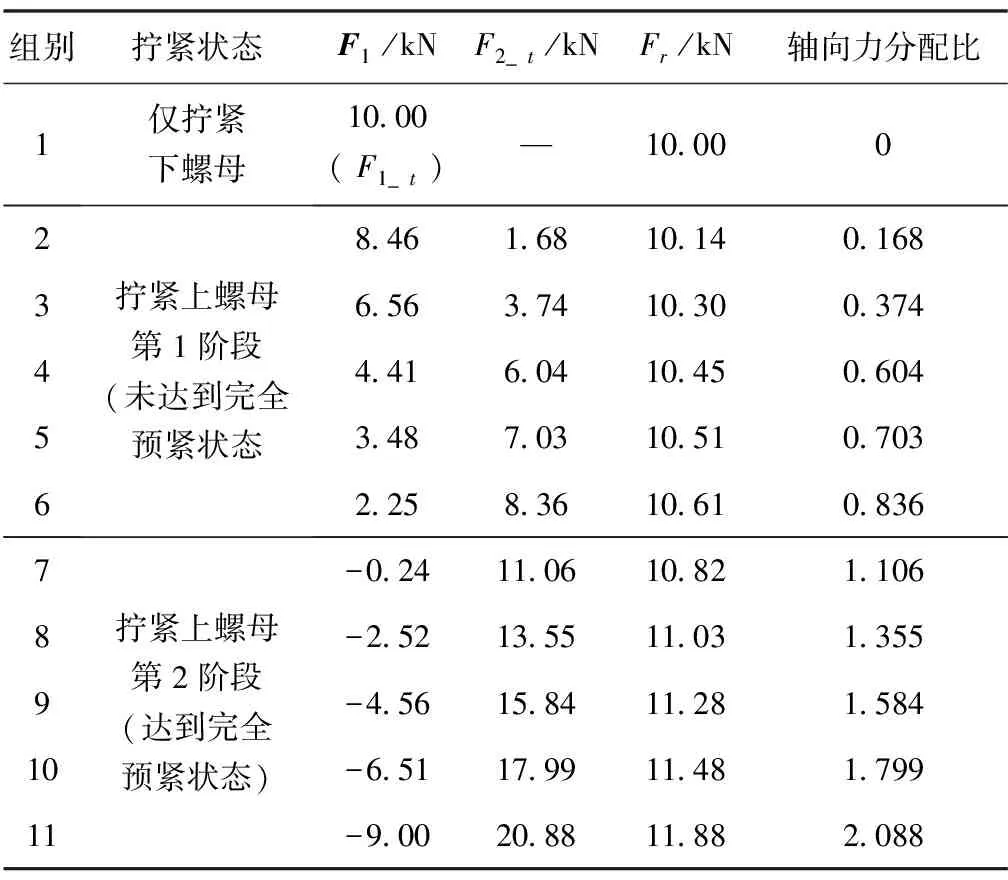
表1 横向振动仿真所用拧紧条件Tab.1 Tightening conditions for transverse vibration simulation

对比第1组和第8组的计算结果，如图10所示。与普通单螺母结构(第1组)的衰减曲线相比，可以看出双螺母结构(第8组)在振动7个周期后,轴向紧固力不再有明显的衰减，而单螺母结构在振动过程中轴向紧固力有持续的衰减；提取螺栓螺纹的接触状态可知，在整个振动过程中，上螺母螺纹上表面与螺栓螺纹下表面始终处于黏结状态(即为静摩擦状态，无界面错动)，说明双螺母结构可以起到很好的防松效果。

图10 振动过程中轴向紧固力及接触状态变化图Fig.10 Variation of axialtightening force and contact state during transverse vibration process

将表1所有情况对应的轴向紧固力衰减曲线汇总，如图11所示。横坐标代表振动周期，纵坐标代表剩余轴向紧固力与第7周期对应的轴向紧固力比值(第6周期后螺栓轴向紧固力开始稳定衰减)。轴向紧固力衰减速率的快慢能够反应双螺母结构防松性能的好坏。

图11 不同轴向力分配情况下轴向紧固力衰减曲线(图例是不同情况所对应的轴向力分配比)Fig.11 Axial tightening force decay curve under different axial force distribution

此处把图11中轴向紧固力衰减曲线的斜率(拟合数据)定义为轴向紧固力的衰减速率，将所有情况下的轴向紧固力衰减速率汇总如图12所示。

分析图12中的结果可知，随着轴向力分配比的增加，防松效果先显著增加后逐渐稳定。当双螺母连接结构在快要达到完全预紧状态时(轴向力分配比约为0.8)，就可以起到很好的防松效果。但本研究得到的定量结论还可能因材料、振幅、温度等因素的影响而发生改变，在工程实际中为了保证防松性能，同时又方便确定拧紧工艺，推荐使用刚好达到完全预紧状态作为目标拧紧状态，根据本文仿真的计算结果，此时轴向力分配比约为1.1(即F2_tF1_t≈1.1)，且有Fr=F2_t，从而可以根据最终的目标预紧力Fr近似确定下螺母预紧力F1_t(即F1_t≈Fr/1.1)。以本文仿真条件为例，材料为45钢，强度等级8.8级的M10螺栓，达到其屈服极限70%的轴向力大约为23kN，若要求拧紧结束后的极限轴向预紧力Fr达到23kN，则可以近似确定F1_t为20.9kN。

图12 轴向紧固力衰减速率汇总曲线图Fig.12 Decay rate of axial tightening force

制定拧紧工艺时还要考虑强度问题，F2_t不能太大，过大将会降低疲劳寿命。如果采用扭矩法控制F1_t和F2_t，则具体的安装扭矩取决于上下螺母各自的扭矩-拉力关系(可通过实验测定)。

5 实验验证

按照国家标准《紧固件横向振动试验方法》[15]，对上下螺母不同轴向力分配情况对双螺母防松性能的影响进行实验验证。具体实验条件如表2所示。

控制F1_t约为20kN，由上述仿真结果可知，刚好达到完全预紧状态时的Fr≈1.1F1_t=22kN。所有实验样本在拧紧结束后的轴向预紧力的统计结果如表3所示，由表3可知，轴向预紧力的值随着上螺母拧紧扭矩的增加而逐渐增加，当拧紧扭等于40N·m时刚好达到完全预紧状态。

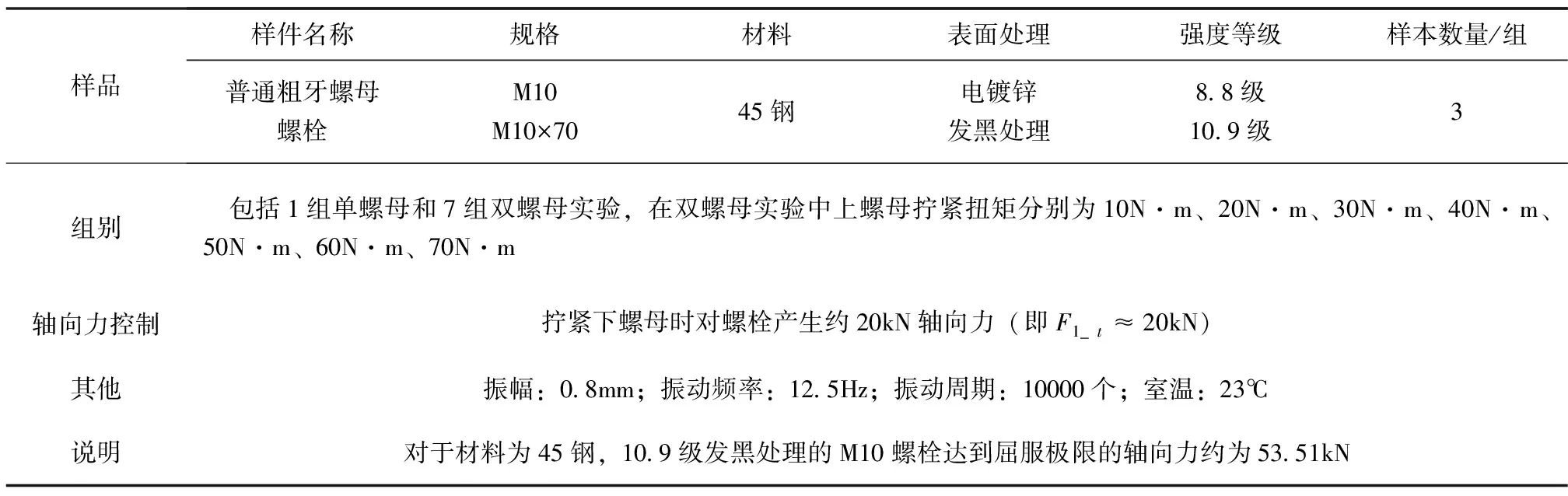
表2 横向振动实验数据汇总Tab.2 Summary of conditions during transverse vibration experiment

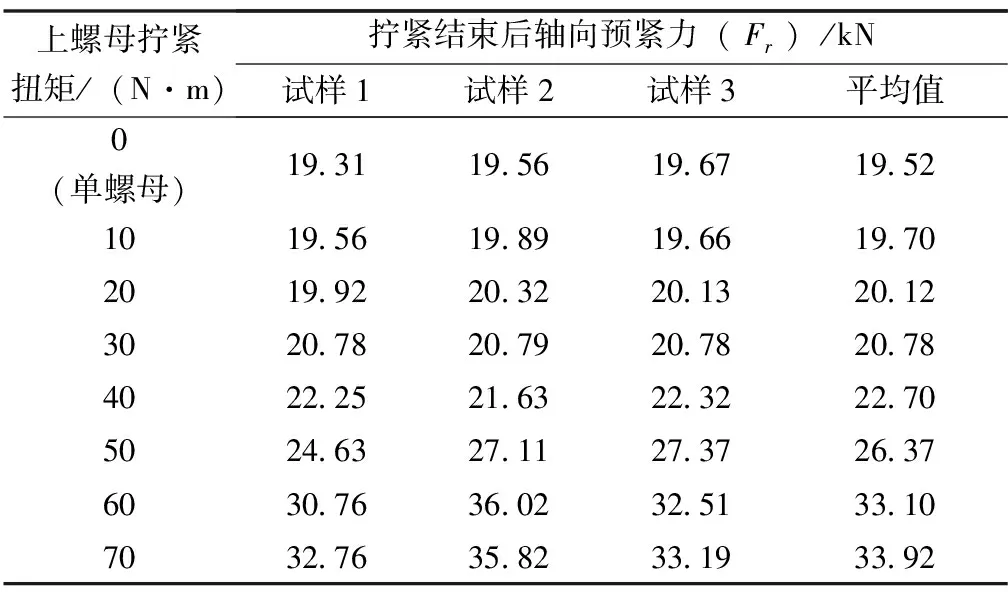
表3 不同分组拧紧结束后轴向预紧力统计结果Tab.3 Statistical results of axial pretension force after screwing upper nut

施加横向振动，统计在10000个周期内轴向紧固力的衰减情况，如图13所示。排除初始振动过程中其他因素的干扰，得到6000个周期到10000个周期对应的轴向紧固力衰减速率(6000个周期后轴向力的变化进入比较稳定的状态)，将不同组别的轴向紧固力衰减速率汇总，如图14所示。由图14可初步判断，大约当上螺母拧紧扭矩超过40N·m时，双螺母连接结构达到完全预紧状态，具有很好的防松性能。图14展示的现象和趋势与仿真结果吻合很好，证明了仿真结果的准确性。

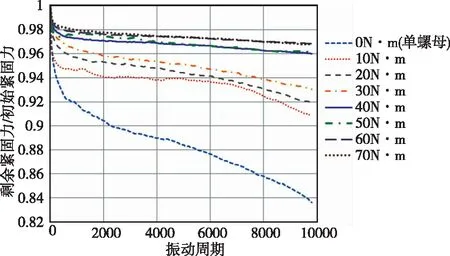
图13 上螺母不同拧紧扭矩对应轴向紧固力衰减曲线图Fig.13 Decay curve of axial tightening force corresponding to upper nut with different tightening torque

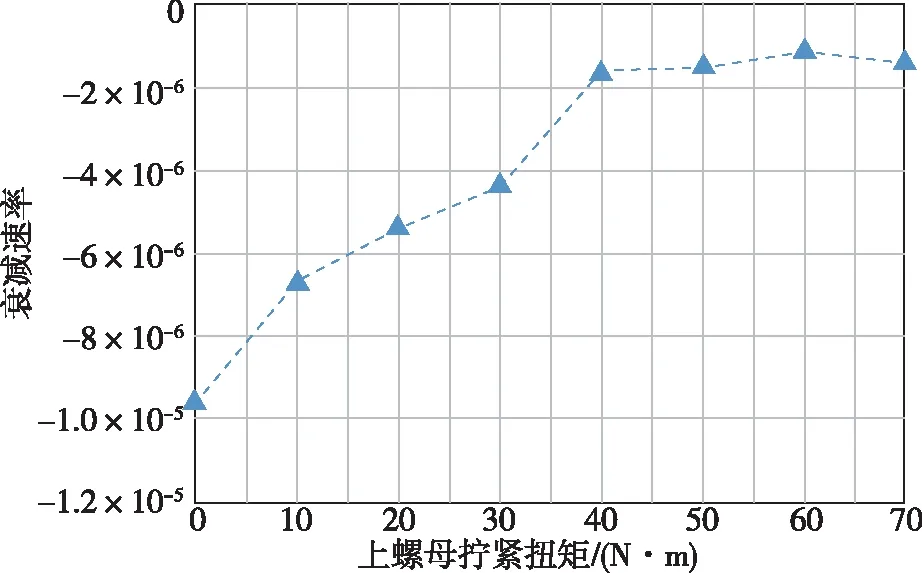
图14 上螺母不同拧紧扭矩对应轴向紧固力衰减速率图Fig.14 Decay rate of axial tightening force corresponding to upper nut with different tightening torque

6 结论

本文利用有限元仿真分析的方法研究了双螺母连接结构上下螺母不同轴向力分配比例对螺栓防松性能的影响。

研究发现，在拧紧过程中，随着上螺母对螺栓产生的轴向力F2的增大，轴向预紧力Fr会逐渐缓慢增大；在松动过程中，当双螺母连接结构快要达到完全预紧状态时，就能够起到很好的防松效果，但在工程实际中为了保证防松性能，需要让双螺母结构达到完全预紧状态。推荐使用刚好达到完全预紧状态时的轴向力分配比(F2_t/F1_t≈1.1)来制定拧紧工艺，此时有Fr=F2_t，可以方便地根据最终目标预紧力Fr近似确定下螺母预紧力F1_t(即F1_t≈Fr/1.1)。如果采用扭矩法控制轴向预紧力，具体的安装扭矩取决于上下螺母各自的扭矩-拉力关系(可通过实验测定)，同时为保证螺栓的强度，上螺母对螺栓产生的最终轴向力F2不能超过螺栓的屈服极限的70%。