传承创新破思维定势 优化拓展显数列特征

山东 王希红

传统的课堂教学，是教师讲，学生听；教师问，学生答；教师写，学生抄.所谓的常用结论，教师让学生死记硬背，做题时，学生就照本宣科，机械模仿.久而久之，禁锢了学生的发散思维和创新意识.导致一听就会，一做就错，或者是稍微创新一些就不会做.其根本原因是还没有深刻的理解数学的本性，要打破思维定势，要有以不变应万变之策.下面笔者用数列几例问题，来切实的反映以上问题症结所在.

一、传承错位相减，创新错位相加

【传承】对一个由等差数列和等比数列对应项之积组成的数列的前n项和，常用错位相减法.形如an=bn·cn,其中{bn}是等差数列，{cn}是等比数列，记Sn=b1c1+b2c2+…+bn-1cn-1+bncn，则qSn=b1c2+…+bn-1cn+bncn+1.

解：Tn=a1+a2·4+a3·42+…+an·4n-1,

4Tn=a1·4+a2·42+a3·43+…+an·4n,

两式相加得,

5Tn=a1+4(a1+a2)+42(a2+a3)+…+4n-1(an+an-1)+4nan,

【创新】本题是类比课本推导等比数列求和公式的错位相减法，学生大部分就照搬课本方法，但是做不出来，因为此题稍微做了创新.注意题目中的条件，突破通法通性，运用错位相加法，即可求得结论.教学中应注重揭示问题的本质,无论是错位相减还是错位相加都是错项相消法.

二、传承裂变差项，创新裂变和项

【传承】裂项相消法实质上是把一个数列的每一项裂变为两项的差，即化为an=f(n)-f(n+1)的形式从而达到求和的目的.

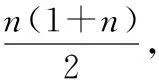
【评析】本例以创业为话题，数学游戏为背景，考查等比数列的基本概念与前n项和公式，考查学生的阅读理解能力与推理论证能力，突出考查由特殊到一般的合情推理与直觉思维能力，通过转化与化归把一般数列化为特殊数列的转化与化归思想.通过部分项列举找出规律，再逐个加以验证，这样思维量少但运算量大，也可以根据题意找到满足条件的关系式，再求解得到结果，但这样需要较强的逻辑推理能力.

(作者单位：宁夏回族自治区固原市回民中学

宁夏回族自治区固原市第二中学)

【例2】(2014·山东卷理·19)已知等差数列{an}的公差为2，前n项和为Sn，且S1,S2,S4成等比数列.

(Ⅰ)求数列{an}的通项公式；

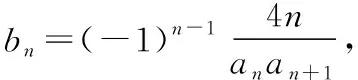
【创新】本题每项不能分解成两项之差，结合条件中公式的特点，运用裂项前和裂项后相等进行检验，故将每项分解成两项之和，裂项相消法的实质是将数列中的每项进行分解，然后重新组合，使之能消去一些项，最终达到求和的目的.可能是和式或差式.

三、传承数列定义，创新隔项问题

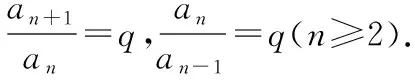
1.隔项成等差

【例3】已知数列{an}满足：a1=20,a2=7,an+2-an=-2(n∈N*).

(Ⅰ)求a3,a4并求数列{an}的通项公式；

(Ⅱ)记数列{an}前2n项和S2n，当S2n取最大值时，求n的值.

解：(Ⅰ)因为a1=20,a2=7,an+2-an=-2(n∈N*)，所以a3=18,a4=5,根据题意可知数列{an}奇数项、偶数项分别是以-2为公差的等差数列.

2013年，美国气象局(NWS)升级了多普勒天气雷达，并且启用了dual-pol技术，该技术可以帮助天气雷达组在第一时间就能辨别出雨水、雪或者冰雹等不同物质，提高了天气预报的实时性和准确度。2014年，NWS开发了一款天气导航工具EDD，该工具可以让用户创建“天气地图”，显示温度、天气状况等信息，并且能够显示出未来一段时间内用户线路上的天气情况(风、雪、雨、雾)等，具体数据(温度、雨雪量、风速等)以及旅行者需要应对或者关心的一些事项。

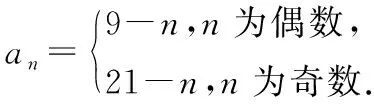
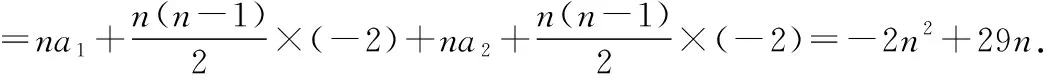
结合二次函数的性质可知，当n=7时S2n取最大值.

2.隔项成等比

【例4】(2015·天津卷理·18)已知数列{an}满足an+2=qan(q为实数，且q≠1),n∈N*，a1=1,a2=2,且a2+a3,a3+a4,a4+a5成等差数列.

(Ⅰ)求q的值和{an}的通项公式；

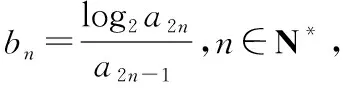
解：(Ⅰ)因为an+2=qan(q为实数，且q≠1)，a1=1,a2=2，所以a3=q,a5=q2,a4=2q，

又因为a2+a3,a3+a4,a4+a5成等差数列，

所以2×3q=2+3q+q2，即q2-3q+2=0，解得q=2或q=1(舍).

所以a3=2,a4=4,根据题意可知数列{an}奇数项、偶数项分别是以2为公比的等比数列.

记数列{bn}的前n项和Sn,

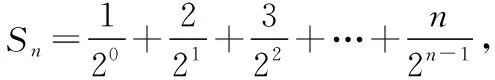
两式相减，得

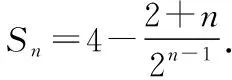
【创新】以上两题在等差、等比数列定义的基础上加以变式创新，an+2-an=-2，an+2=qan(q为实数)，这类问题可以理解为隔项等差数列和隔项等比数列，或双等差数列和双等比数列.处理这类问题应分奇数和偶数讨论，在求通项时要分别找出每一组的首项，然后注意公差(公比)和项数的关系，还是套用等差、等比数列的通项公式.拓展延伸，隔两项、三项都可以.