“超级全能生”2018高考全国卷26省12月联考乙卷数学(文科)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={x|x2-x-6<0},B={x|2x<1},则A∩B=
( )
A.(-∞,3) B.(0,3) C.(-2,3) D.(-2,0)
2.复数z满足z·i=3-i,则复数z的虚部为
( )
A.-1 B.3 C.-3 D.-3i

( )

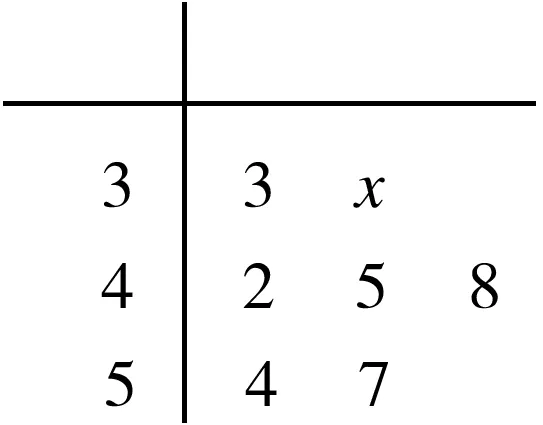
4.某人用手机软件记录自己一周内每天体育锻炼的时间(单位:分钟),绘制茎叶图如图所示,已知这组数据的平均数是45,则中位数和x的值分别为
( )
A.45和6 B.45和9
C.44和6 D.44和9

( )
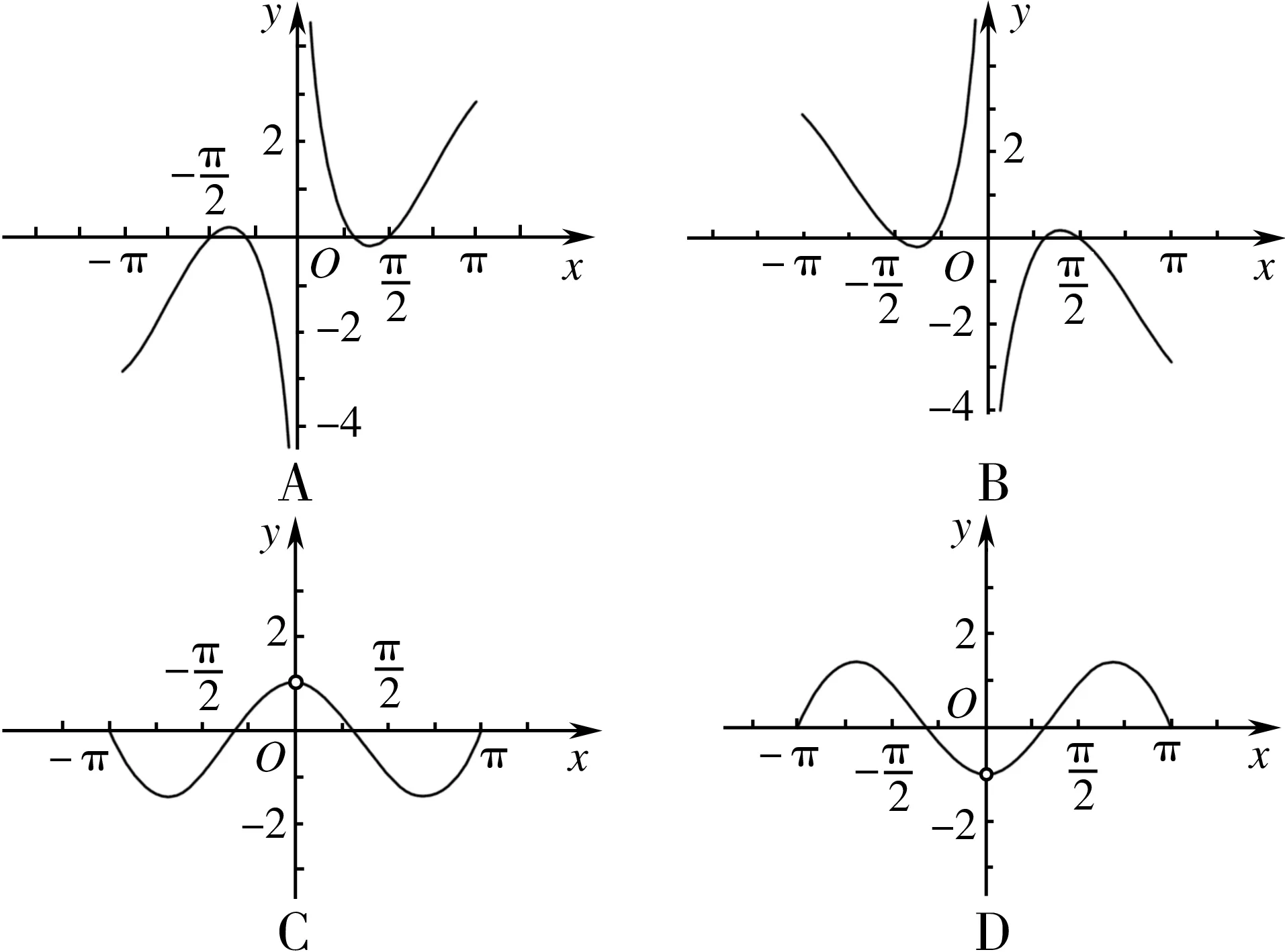

( )
A.64 B.8 C.16 D.32

7.魏晋时数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”.刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比为π∶4.若已知正方体的棱长为2,则“牟合方盖”的体积为
( )

8.图中的程序框图所描述的算法是计算著名的数列“斐波那契数列”中的项,若输入的k=20,则输出n的值为
( )
A.7
B.8
C.9
D.10
9.以抛物线x2=my上的点P(1,-1)为圆心且与抛物线的准线相切的圆的标准方程是
( )
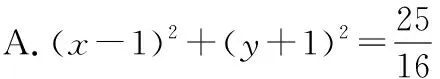
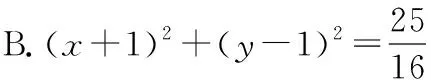
C.(x-1)2+(y+1)2=4
D.(x+1)2+(y-1)2=4
10.某几何体的三视图如图所示,则该几何体的表面积为
( )
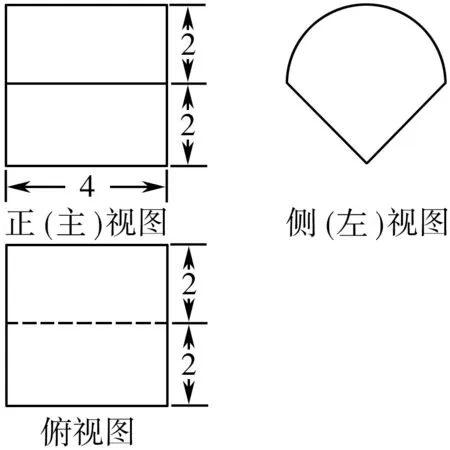
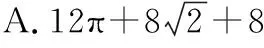

11.下列命题正确的是
( )

(2)由图象求正弦型函数y=Asin(ωx+φ)的解析式时,振幅A的大小是由一个周期内的图象中的最高点的值与最低点的值确定的;
(3)函数f(x)=Asin(ωx+φ)的图象的两个相邻对称轴间的距离为一个最小正周期;
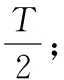
A.(1)(2)(4)(5) B.(1)(2)(4)
C.(1)(5) D.(2)(3)(4)(5)
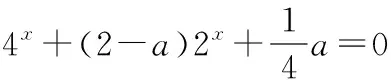
( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
二、填空题:本题共4小题,每小题5分,共20分.





16.如图,某地方政府为改善当地的交通状况,计划在AB之间的山中修建一条隧道,公路AD与BC上都有村庄,工程预算人员选了一条离这座山最近的公路CD进行测量,得到如下数据:DC=10 km,∠ADB=75°,∠BDC=60°,∠ACB=60°,∠ACD=15°,则线段AB的长度为________.(结果可以保留根号)
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
已知函数f(x)=x2-5x+1,设数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在函数f(x)的图象上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{2an}的前n项和Tn.
18.(12分)
已知AB是圆O的直径,PA垂直于圆O所在的平面,点C为圆O上一点,AB=6,PA=4,∠ABC=30°,AE⊥PC,点F为PB的中点.
(Ⅰ)求证:AE⊥平面PBC;
(Ⅱ)求多面体ABCEF的体积.

19.(12分)
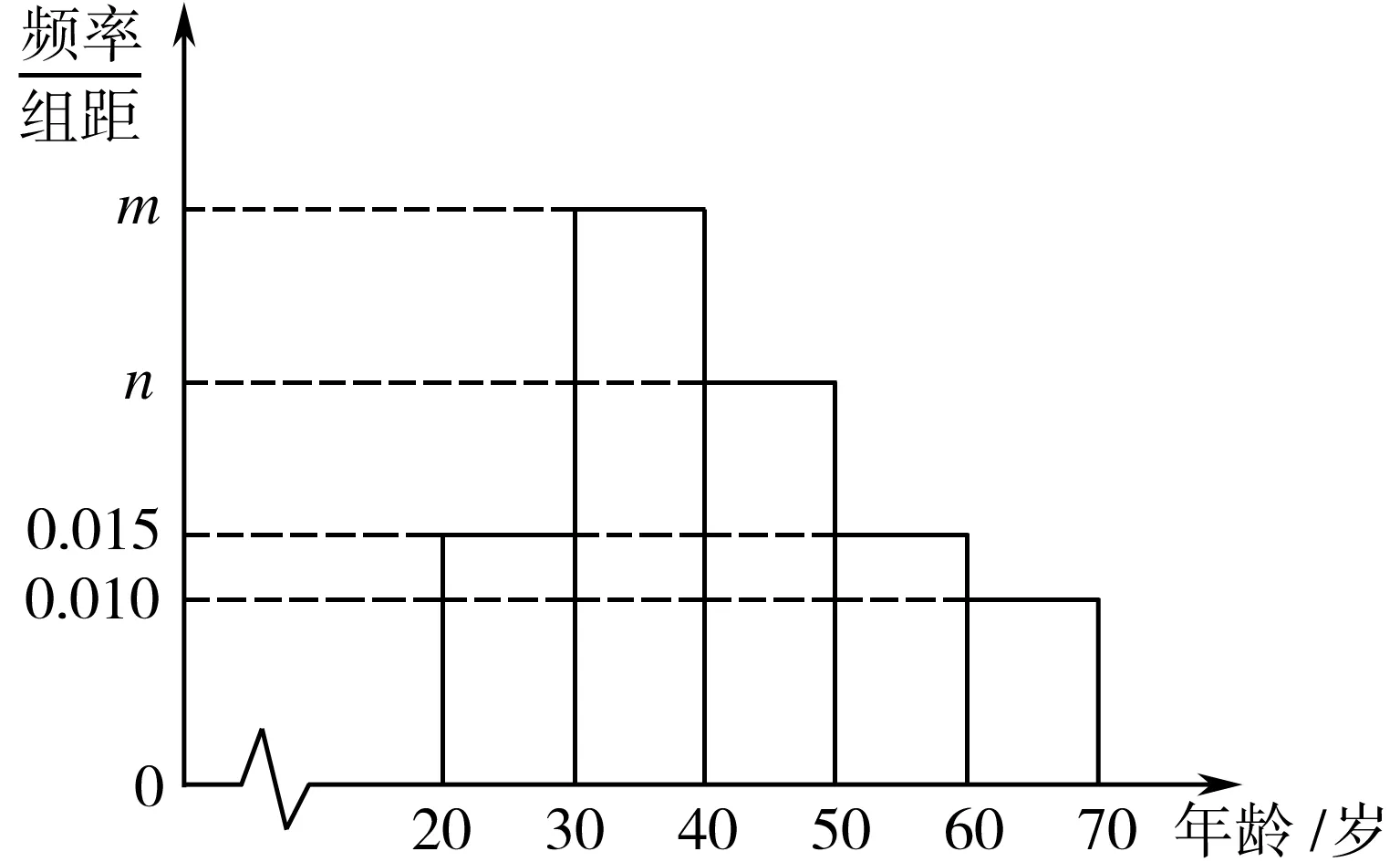
根据淘宝、天猫的调查统计显示,调查的100名网购者的年龄(单位:岁)情况如图所示,已知中间三个年龄段的网购者人数成等差数列.将高于50岁的网购者称为“老年网购者”,并将有关性别的信息统计到表中.

“老年网购者”非“老年网购者”合计男1030女合计
(Ⅰ)根据图表信息,判断是否有95%的把握认为“老年网购者”与性别有关?
(Ⅱ)为鼓励大家网上购物,该平台常采用购物就发放代金券的方法进行促销,具体做法如下:年龄在[30,50)岁的每人发放20元,其余年龄段的每人发放50元,现按发放代金券的金额采用分层抽样的方式从参与调查的100名网购者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率;
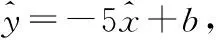
①b=1 310;
②由于回归方程的斜率是负的,说明年龄越大的网购者,每周消费金额一定越少;
③由于回归直线方程的斜率是负的,说明两个变量的相关关系是负相关;
④回归直线是所有直线中穿过数据点最多的直线;
⑤能够算出回归方程,说明两个变量之间确实是线性相关关系.
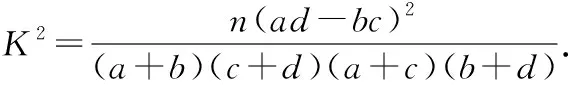

P(K2≥k)0.0500.0100.001k3.8416.63510.828
20.(12分)
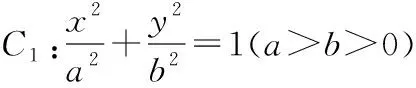
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设点A,B,Q是点P分别关于两坐标轴及坐标原点的对称点,平行于AB的直线l交C1于异于P,Q的C,D两点,点C关于原点的对称点为点E.证明:直线PD,PE的倾斜角互补.
21.(12分)
已知函数f(x)=xex+a(x+1)2,其中a≥0.
(Ⅰ)求函数f(x)的单调区间;

(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,则按所做的第一题记分.
22.[选修4-4:坐标系与参数方程](10分)
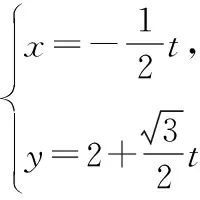
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)若直线l与圆C交于A,B两点,求弦长|AB|.
23.[选修4-5:不等式选讲](10分)
已知函数f(x)=|2x+1|+|x-1|.
(Ⅰ)求不等式f(x)≥3的解集;

参考答案
1.D 2.C 3.B 4.A 5.D 6.B 7.C 8.B 9.A 10.C 11.A 12.B
17.解:(Ⅰ)因为点(n,Sn)在函数f(x)的图象上,
所以Sn=n2-5n+1.
当n=1时,a1=S1=1-5+1=-3;
当n≥2时,an=Sn-Sn-1=n2-5n+1-[(n-1)2-5(n-1)+1]=2n-6;
当n=1时,a1≠2-6=-4,
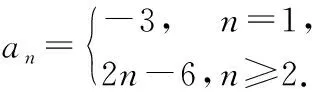
(6分)
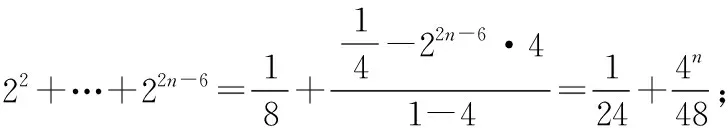
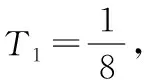
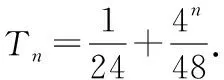
(12分)
18.解:(Ⅰ)证明:∵AB是圆O的直径,点C为圆O上一点,∴AC⊥BC,
又∵PA垂直于圆O所在的平面,BC在圆面上,
∴PA⊥BC,
又∵PA∩AC=A,∴BC⊥平面PAC,
∵AE⊂平面PAC,∴BC⊥AE,
又∵AE⊥PC,PC∩BC=C,∴AE⊥平面PBC.
(5分)
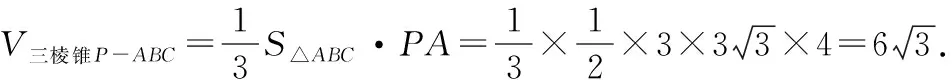
在Rt△PAC中,∠PAC=90°,PA=4,AC=3,

在Rt△PCB中,∠PCB=90°,
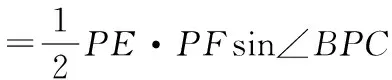
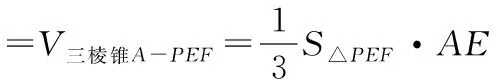

(12分)
19.解:(Ⅰ)由频率分布直方图知“老年网购者”的频率为 0.25,则调查的100名网购者中有25人是“老年网购者”,得2×2列联表为
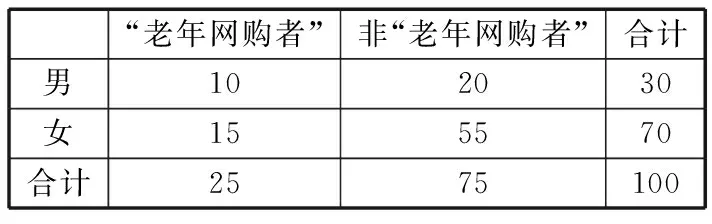
“老年网购者”非“老年网购者”合计男102030女155570合计2575100
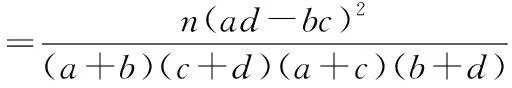
故没有95%的把握认为“老年网购者”与性别有关.
(4分)
(Ⅱ)由频率分布直方图可知m+n=0.1-0.015×2-0.01=0.06,
∵中间三个年龄段的网购者人数成等差数列,
∴m+0.015=2n,
故可解得m=0.035,n=0.025.
利用分层抽样的方式从100名网购者中抽取5人,
根据频率分布直方图,可得年龄在[30,50)岁的频率为10×0.035+10×0.025=0.6,
因此抽取的5人年龄在[30,50)岁的人数为5×0.6=3,
记为A1,A2,A3,其余年龄段的有2人,记为B1,B2,
从这5人中抽取3人所有等可能的情况有A1A2A3,A1A2B1,A1A2B2,A1A3B1,A1A3B2,A2A3B1,A2A3B2,A1B1B2,A2B1B2,A3B1B2,共10种,
3人获得代金券的金额总和为90元的取法有A1A2B1,A1A2B2,A1A3B1,A1A3B2,A2A3B1,A2A3B2,共6种,
(8分)
(Ⅲ)∵网购者年龄的平均数为0.15×25+0.35×35+0.25×45+0.15×55+0.10×65=42,
∴1 100=-5×42+b,∴b=1 310,∴①正确;
由于回归方程的斜率是负的,说明年龄越大的网购者,每周平均消费金额会越少,但不是一定变少,∴②错误;
由于回归直线方程的斜率是负的,说明两个变量的相关关系是负相关,∴③正确;
∴④错误;
能够算出回归方程,不能说明两个变量之间确实是线性相关关系,两个变量是不是成线性相关关系还要看相关系数的大小,∴⑤错误.
故①③正确,②④⑤错误.
(12分)

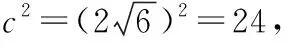
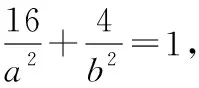
解得a2=32,b2=8,

(5分)
(Ⅱ)证明:A,B,Q是P(-4,2)分别关于两坐标轴及坐标原点的对称点,可设A(-4,-2),B(4,2),Q(4,-2),
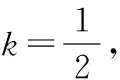
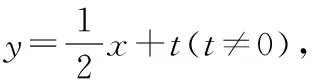
代入椭圆x2+4y2=32,可得x2+2tx+2t2-16=0,
即有Δ=4t2-4(2t2-16)>0,解得-4 设C(x1,y1),D(x2,y2),则E(-x1,-y1), x1+x2=-2t,x1x2=2t2-16, 设直线PD,PE的斜率分别为k1,k2, 要证直线PD,PE的倾斜角互补,只需证k1+k2=0, 即证(4-x1)(y2-2)-(x2+4)(y1+2)=0, 可得(4-x1)(y2-2)-(x2+4)(y1+2)=-x1x2-t(x1+x2)-16=-(2t2-16)+2t2-16=0, 所以直线PD,PE的倾斜角互补. (12分) 21.解:(Ⅰ)因为f(x)=xex+a(x+1)2, 所以f′(x)=(x+1)ex+2a(x+1)=(x+1)(ex+2a), 因为a≥0,所以ex+2a>0,令f′(x)>0,解得x>-1; 令f′(x)<0,解得x<-1, 所以f(x)的单调递增区间是(-1,+∞),单调递减区间为(-∞,-1). (5分) (Ⅱ)证明:由(Ⅰ)可知,f(x)=xex+a(x+1)2在区间(-1,+∞)上单调递增,在区间(-∞,-1)上单调递减,不妨设x1<-1 令F(x)=f(x)-f(-2-x) =xex+a(x+1)2-[(-2-x)e-2-x+a(-x-1)2] =xex+(x+2)e-2-x(x<-1), 因为F′(x)=(x+1)(ex-e-x-2)>0, 所以F(x)在(-∞,-1)上单调递增, 所以F(x) 所以f(x) 所以f(x2)=0=f(x1) 因为-2-x1>-1,x2>-1,f(x)在(-1,+∞)上单调递增,所以x2<-2-x1, (12分) 22.解:(Ⅰ)圆C的极坐标方程为ρ=4cosθ, 可化为ρ2=4ρcosθ, 可得其直角坐标方程为x2+y2-4x=0, 配方得(x-2)2+y2=4. (5分) 设A,B对应的参数分别为t1,t2, (10分) ∴f(x)≥3的解集为{x|x≤-1或x≥1}. (5分) (10分)