改进的经验模态分解法去除脉搏波基线漂移

，，，

(1.中国民航大学 中欧航空工程师学院，天津 300300；2.中国民航大学 天津市智能信号与图像处理重点实验室，天津 300300)

0 引言

人体心脏有规律的收缩和舒张，将血液不断输向周围血管，引起血管壁产生规律的振动，这个振动可以在皮肤的浅动脉处获得，即为脉搏波[1]。从脉搏波信号中可以提取到非常丰富的人体生理病理参数，对于疾病诊治有着非常重要的参考价值[2]。然而，人体脉搏波信号非常微弱，利用光电容积法对脉搏波进行采集、放大以及模数转换的过程中，脉搏波非常容易受到干扰，使脉搏波信号淹没到较强的背景噪声中。为了能从光电容积法采集到的脉搏波中准确提取出血压、血氧等人体生理参数，需要对其进行预处理，去除噪声的影响。

研究发现，采集到的脉搏波中主要存在肌电干扰、基线漂移和高频噪声等干扰噪声[3]。在采集脉搏波的过程中，测试者肌肉发生抖动产生肌电干扰，具有随机性，频谱特性和白噪声相似。基线漂移是由测试者的呼吸运动和与皮肤接触时不同的受力产生的，频率一般在0.2～0.3 Hz，属于低频干扰噪声[4]。高频噪声主要是随机噪声和环境干扰，如电子设备产生的热噪声，且噪声幅度随环境变化而改变[5]。脉搏波中高频噪声和肌电干扰的去除在文献6中已经有具体有效的研究[6]，本文研究脉搏波中基线漂移的去除。

去除脉搏波信号中基线漂移的方法主要有：FIR和IIR低通滤波器、时变滤波器、多项式插值法、中值滤波法[7]。FIR和IIR滤波器均属于低通滤波方法，该类方法对高于截止频率的噪声无法去除，截止频率设置太高，信号会产生失真[8]。Sommo等人设计时变滤波器来去除信号中的基线漂移，但实现比较复杂并且依赖于心率的精确测定[9]。多项式插值法需要先确定"基准点"，而基准点的精确查找是一个学术难题，至今没有有效的方法[10]。中值滤波法在滤除基线漂移的同时容易造成脉搏波信号的失真[11]。

黄锷等人提出了经验模态分解(Empirical Mode Decomposition，EMD)法，用于处理非线性、非平稳信号，脉搏波信号通过EMD自适应分解，可以表示为一组固有模态函数(Intrinsic Mode Function，IMF)之和的形式[12]。通过去除部分IMF分量的方式实现对信号的基线漂移去除。在如何确定IMF分量保留阶数的问题上通常有两种方法：其一是采用小波变换阈值法的思想设置相应的阈值进行判断，将低于阈值的IMF分量全部置为零，然后进行信号重构[13]。然而EMD分解和小波变换有着本质的不同，此外阈值选择方法容易造成脉搏波信号的失真。其二是经验法，脉搏波信号通过EMD自适应分解得到的IMF分量，频率从高到低，基于经验将后几个IMF分量直接丢弃掉，将剩余IMF分量进行重构得到去除基线漂移后的脉搏波。此方法并不能很有效地判断出哪个或者哪几个IMF分量为噪声部分，尤其是当实际含噪信号很复杂时，此方法性能下降。

本文提出一种基于过零率检测的EMD方法去除脉搏波信号基线漂移的新方法。该方法将EMD自适应去噪和低通滤波器有效结合，根据过零率检测筛选出脉搏波基线信号IMF分量的阶数，设计低通滤波器从这些IMF分量中估计出基线漂移信号，原始脉搏波信号减去基线漂移信号实现基线漂移的去除。实验结果证明，该算法科学合理，减少了经验判断造成的误差，不仅去除了脉搏波信号中基线漂移的干扰，同时也避免了脉搏波信号的失真。

1 问题提出

经验模态分解法实际上是对非平稳信号进行平稳化处理，把信号中不同尺度的波动或趋势逐层分解，生成一组含有不同特征尺度的IMF分量[14]。含有噪声的脉搏波x(t)信号通过EMD自适应分解可以表示为N个IMF分量和一个残余分量之和：

(1)

其中fn(t)表示第n个IMF分量，r(t)表示残余分量。IMF分量必须符合如下两个要求[15]：其一是每阶IMF分量中，极值点和过零点个数一样或者最大相差1个，即两个相邻极值点之间必有一个过零点；其二是任意时刻内，IMF分量关于时间轴对称，极大值和极小值点组成的上下包络线平均值为零。残余分量可能是一个常数或者一个单极值点函数，表示信号的主要走向趋势。获取IMF分量的过程为[15]：首先使用三次样条插值法对脉搏波信号x(t)的上下极值点进行拟合得到上、下包络线，记上下包络线的均值为m1(t)。用脉搏波信号x(t)减去m1(t)，得到去除低频趋势的信号h1(t)，即：

h1(t)=x(t)-m1(t)

(2)

通常得到的h1(t)不一定就是满足条件的IMF，因此需要对h1(t)重复上述过程，得到h1(t)的上下包络线均值为m11(t)，则记去除h1(t)低频趋势后的信号为h11(t)，即：

h11(t)=h1(t)-m11(t)

(3)

重复(2)-(3)过程，直到求出满足要求的第一个IMF分量，记为f1(t)，表示信号的高频成分。用x(t)减去f1(t)，得到待分解信号r1(t)，对r1(t)按照上述过程继续分解，得到第二个满足要求的IMF分量，记为f2(t)。在得到N个IMF分量后，剩余的残余分量为单调函数或直流信号时，分解结束，即：

r1(t)=x(t)-f1(t)

(4)

ri(t)=ri-1(t)-ci(t)i=1,2,…,N

(5)

脉搏波信号通过EMD自适应分解得到的IMF分量是单分量信号，即每个时刻只有一个瞬时频率，表示信号的内在特征振动形式。各IMF分量分别代表信号从高到低不同频率段的成分，信号中的高频部分在前几个IMF分量中，低频部分和干扰噪声主要位于后面几个高阶IMF分量。脉搏波信号中的基线信号部分位于高阶的IMF分量中，如何确定脉搏波基线信号所在的IMF分量阶数是本文算法的核心问题。

2 阶数选择

EMD方法去噪主要是使用特定的噪声评判标准对IMF分量的属性进行判断，认为是噪声则进行相应的去除或者处理。一般用来作为评判的标准有相关性分析、信息熵、标准差、连续均方差等[16]。本文使用过零率检测作为基线漂移固有模态分量选择的评判标准。过零率是指单位时间内信号过零点的个数。对于复杂微弱的生物信号如脉搏波信号，信号幅度大小对过零率的影响甚微，并且过零率不受外界环境的干扰，因此干扰噪声的过零率与纯净的脉搏波信号的过零率有着很大的不同。研究结果表明，对于一个平稳的高斯随机信号，频带范围从fL到fH，过零点的个数M与功率谱密度p(f)的关系如下所示：

(6)

脉搏波信号通过EMD自适应分解得到的一组IMF分量，根据IMF满足的条件可知，IMF分量拥有关于时间轴对称的特性，说明每阶IMF分量都含有过零点，并且两个相邻的极值点之间必有一个过零点。同时，这也说明每阶IMF分量中不含有其它复杂的叠加波，这进一步加强了过零率与频率之间的关系。因此选择将过零率作为脉搏波EMD分解基线信号所在的IMF分量选择的评判标准，设定阈值，将阈值范围内的IMF分量进行重构实现脉搏波的去噪。

3 算法步骤

通过过零率检测确定脉搏波信号的基线信号IMF分量阶数为m，如果将m阶及其之后的IMF分量直接丢掉然后重构得到的信号，虽然可以去除基线漂移，但是会造成脉搏波信号有用部分的损失，因为高阶IMF分量中也同时含有脉搏波信号的低频成分。因此，还需要设计一个低通滤波器，得到真实的基线漂移信号。用原始脉搏波信号减去基线漂移信号，得到纯净的脉搏波信号。本文提出的基于过零率检测的EMD方法去除脉搏波的基线漂移算法的主要步骤总结如下：

1)对含有基线漂移的原始脉搏波x(t)进行EMD自适应分解，得到IMF分量f1(t),f2(t),…,fn(t)及其残余分量r(t)；

2)计算每阶IMF分量及残余项r(t)的总过零率，筛选出低于阈值的IMF分量，确定脉搏波基线信号的IMF分量阶数m；

3)将m阶及之后的IMF分量进行重构得到重构信号y(t)，将y(t)通过低通滤波器得到基线漂移估计信号n(t)；

4)用原始脉搏波信号减去基线漂移估计信号n(t)，得到去除基线漂移后的脉搏波信号x′(t)。

4 实验

在反射的测量方式条件下，脉搏波采集装置采用欧司朗公司研制的SFH7051光电传感器，以新唐公司的ARM MINI58为核心处理器，采集静止状态下的人体脉搏波。图1是采集到的一组基线漂移非常严重的脉搏波。

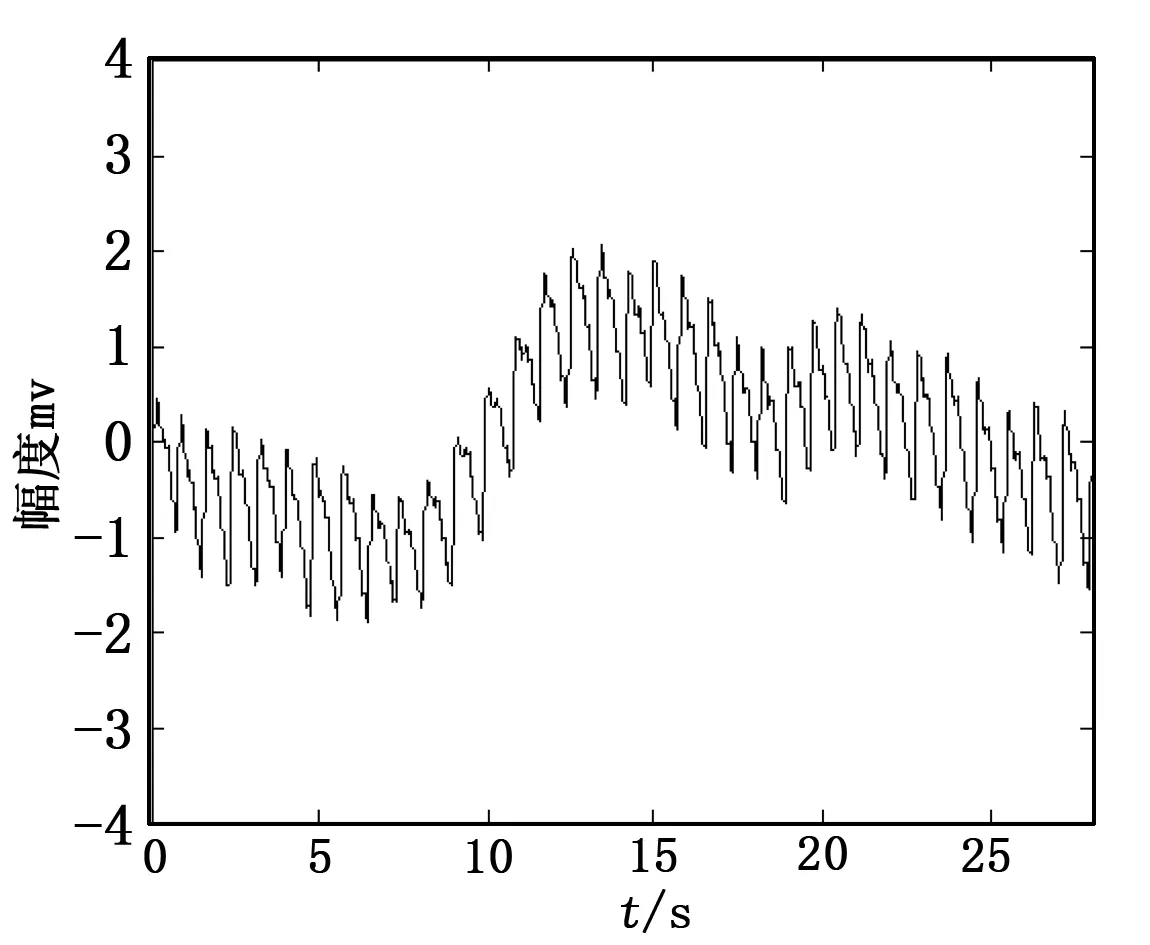
图1 原始脉搏波信号

对图1所示的脉搏波进行EMD自适应分解，得到10阶IMF分量和1阶残余分量，如图2所示。本文定义每阶IMF分量中所有过零点的个数与IMF分量长度的比值为总过零率。计算各阶IMF分量的总过零率如图3所示。从图3中可以明显看出，IMF分量中f1(t)～f3(t)的总过零率是在一个数量级范围内，相对较高，并且图2中可以看出时域内相应的IMF分量波形变化剧烈有白噪声特点，可以认为是高频噪声干扰成分，予以去除；f4(t)～f6(t)是脉搏波的有效成分，予以保留；f7(t)～f10(t)的总过零率在一个数量级范围内，相对较小，认为是脉搏波的基线信号成分。因此将阈值设为0.01，对IMF分量进行筛选，得到脉搏波的基线信号阶数为7。重构f7(t)～f10(t)得到脉搏波的基线信号如图4所示。

图2 脉搏波EMD自适应分解图

图3 每阶IMF分量的总过零率

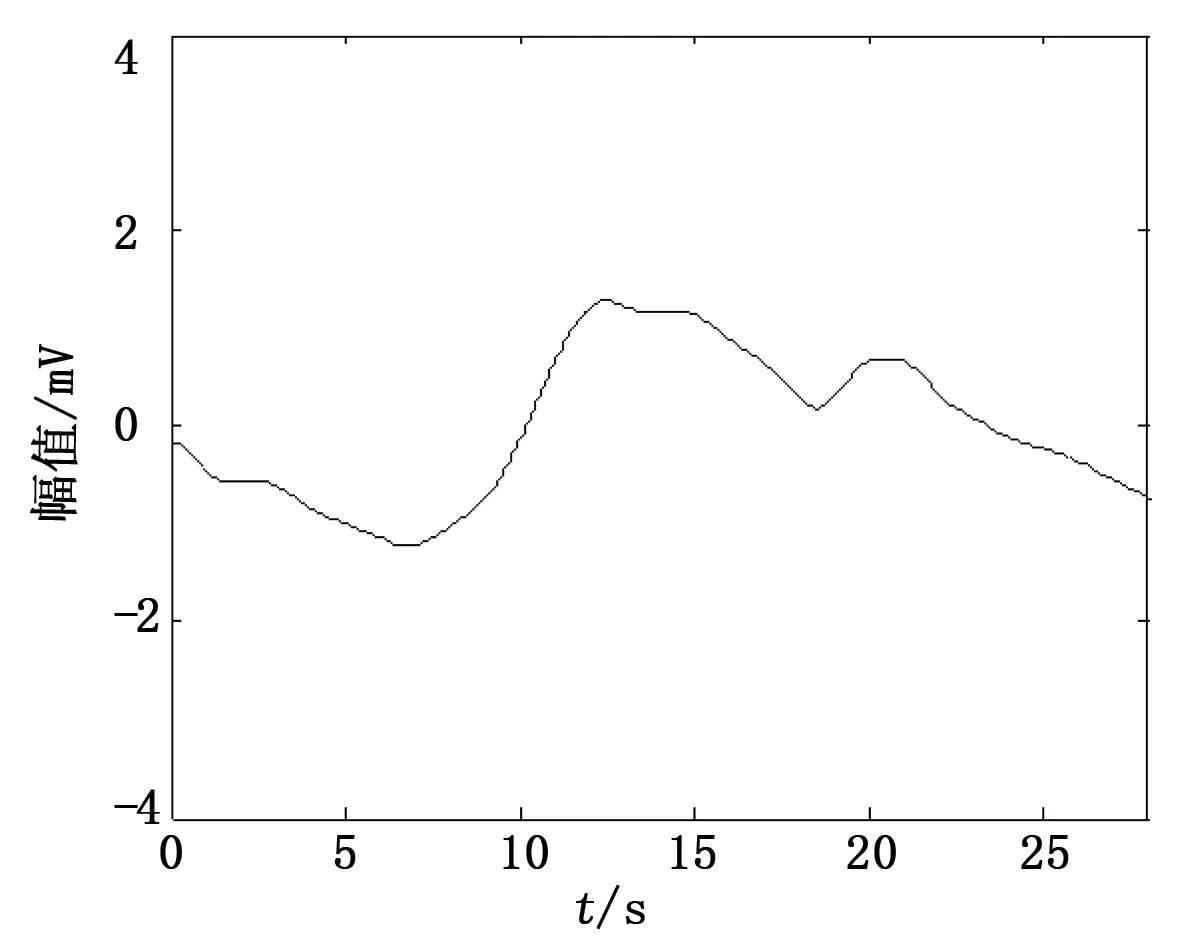
图4 脉搏波的基线信号

基线漂移是低频干扰噪声，频率很低，因此对对原始脉搏波信号和脉搏波基线信号进行傅里叶变换，对比二者的频谱，如图5所示。

观察图5可以发现，基线信号和脉搏波信号在0.6 Hz以下的频谱图基本吻合，特别是在干扰噪声频谱图比较突出的0.1345 Hz和0.243 7 Hz处，这表明我们提取的基线信号就是脉搏波的低频噪声，但是仔细观察发现，重构得到的基线信号在1 Hz以上的频率处幅值并不为0，如1.2534 Hz处，还存有脉搏波有效的低频成分。所以可以断定，如果直接将重构得到的基线信号去除那么势必会造成脉搏波信号的失真。因此本文设计了一个截止频率为0.8 Hz的IIR巴特沃斯低通滤波器，利用其通频带内平坦的优势，将基线信号通过该低通滤波器后得到真实的基线漂移信号。

使用本文算法、EMD经验法、EMD阈值法得到去除基线漂移后的脉搏波如图6所示。通过对比图6和图1，从中可以明显观察出三种方法基本上都实现了脉搏波基线漂移的去除。然而仔细观察可以发现，本文算法处理过后的脉搏波整体比较平稳，基线漂移得到了明显去除。而EMD阈值法处理过后的脉搏波，在14～20 s处还存在很明显的基线漂移，EMD经验法在25～28 s处也存在基线漂移。为了更为准确地对比三种方法去噪的优劣，还需要进一步讨论。

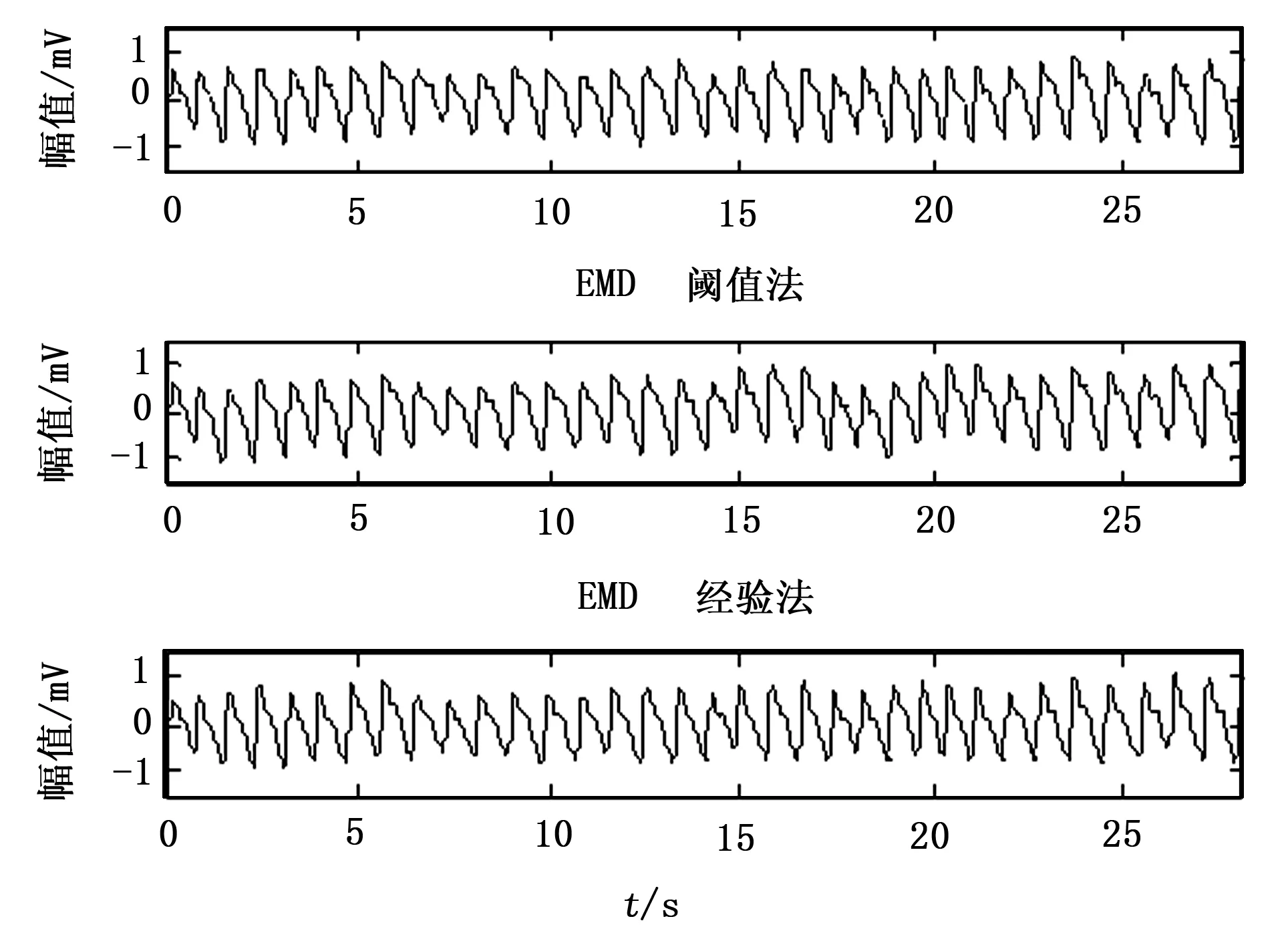
图6 三种方法得到的去除基线漂移后的脉搏波

5 仿真结果与讨论

观察图6发现，三种方法都实现了脉搏波基线漂移的去除，为了能够客观对比出三种方法去噪的优劣，需要确定一个参数进行判断。由于脉搏波为等幅信号，因此选择将去除基线漂移后的脉搏波的上下包络线的均值b(t)作为去噪效果评价参数，b(t)越平稳，说明去噪效果更好。从图7中可以明显的看出，本文算法得到的上下包络线均值相比其它方法更加平稳，去噪效果最好。

图7 三种去噪算法得到的脉搏波上下包络线均值图

在信号处理领域中，通常采用信噪比SNR和均方根误差RMSE两个参数判断去噪的好坏。通常，SNR值越大，RMSE值越小，说明去噪效果越好。假设f(n)为去除基线漂移后的脉搏波，f′(n)为原始脉搏波信号，基线漂移信号为e(n)，可得：

f′(n)=f(n)+e(n)

(7)

信噪比(SNR)定义如下：

(8)

均方根误差(RMSE)定义如下：

(9)

三种方法去除基线漂移后的脉搏波的信噪比和均方根误差结果如表1所示。从表1中可以得到，本文提出的算法信噪比比EMD阈值法、EMD经验法的信噪比分别提升了28.1%、5.7%。同时，均方差分别减小了24.8%、17.5%，得到了更好的去噪效果。去除基线漂移后的脉搏波便于下一步对脉搏波信号特征值的准确提取。

表1 三种方法去除基线漂移后的SNR和RMSE

6 总结

脉搏波信号是人体生物信号中典型的非平稳、非线性信号。基线漂移是采集过程中常见的干扰噪声之一。本文提出的基于过零率检测的EMD方法去除脉搏波的基线漂移，首先通过过零率检测筛选出脉搏波的基线信号，利用自行设计的低通滤波器得到真正的基线漂移信号，最后用原始脉搏波信号减去基线漂移信号得到纯净无干扰的脉搏波。实验结果表明，该方法不仅去除了基线漂移对脉搏波信号的干扰，而且尽可能地保留了完整的脉搏波信息，提高了脉搏波信号的信噪比，对无创血压测量和人体生理参数的精确提取具有重要意义。