基于OTT策略的可变力度组合测试用例优先级排序方法
,, ,,
(1.浙江理工大学 信息学院, 杭州 310018; 2.山口大学 东亚研究科, 日本 山口 753-8513)
0 引言
组合测试已广泛应用于软件测试中,该方法能够缩减测试用例的规模[1]。由于软件产品更新换代的频率逐渐上升,对组合测试用例进行完全测试的成本不断增加[2]。针对此问题,将优先级技术[3-4]引入到组合测试内,能够在软件测试过程中,提高测试效率。Kuhn等人[5]发现组合测试中,两个参数相互组合所生成的用例可以检测出70%的错误,90%以上的错误可由三个以内参数相互组合找出。围绕组合测试用例优先级排序问题已有相应研究:Bryce等人[6]利用单一组合覆盖信息实现组合测试用例的排序问题;黄如兵等[7]从多重组合覆盖情况角度保证测试的有序进行;王子元等[8]提出了以组合权重和测试代价为标准的组合测试用例优先级排序的方法。
目前,针对可变力度的组合测试用例优先级排序方法的研究仍然较少,排序过程中组合力度选取困难,且当前固定力度组合测试用例的优先级排序方法无法满足复杂的交互关系,因此结合局部组合覆盖率、测试用例失效率和测试用例的重要程度,避免优先级排序因素单一;利用测试过程中的反馈信息,实现优先级在线排序;本文提出了一种基于OTT策略思想的可变力度组合测试用例优先级在线排序方法。
1 优先级排序因素
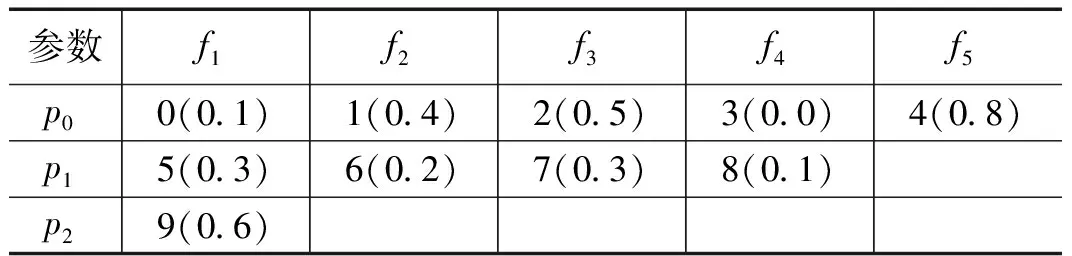
待测软件系统(Software Under Test,SUT)中,组合测试内部影响因子的相互关系并非完全一致,部分影响因子之间的相互作用可能更加紧密[9],仅依靠固定力度的组合测试优先级排序方法无法满足影响因子之间这种复杂的交互关系。假设存在n个影响因素,这些影响因子构成一个有限集合F={f1,f2,…fn},其中每个影响因素fi的取值为vi={p1,p2,…pj}。那么,SUT的一条测试用例tc={x1,x2,…xn}(x1∈v1,x2∈v2,…xn∈vn)。为了更好地描述可变力度组合测试用例优先级排序方法,对本文出现的相关概念进行如下描述:初始测试用例序列St0表示组合测试用例排序之前,测试用例序列的集合,一般为φ。初始测试用例集Tt0={tc1,tc2,…tcN}是针对SUT,根据组合测试方法及可变强度覆盖表VSCA(N,λm,n,F,CA(N′,λs,n′,F′))生成的测试用例集合。显然,1≤λm<λs≤|F′| 可变力度的组合测试用例优先级中,需考虑组合覆盖率的影响。然而,如何在影响因子集下选取一个合适的组合力度作为衡量组合覆盖率的标准成为了难题。研究表明[7]:若选取λm为组合覆盖力度,当覆盖了所有λm组合后,优先级的选取演变成了随机排序方式;若选取λs为组合覆盖力度,则忽略了影响因子集F′中λm的组合覆盖情况;若选取的组合覆盖力度介于λm与λs之间,则面临了上述两种问题。故根据不同的组合覆盖力度,需考虑不同局部影响因子集下组合测试用例的组合覆盖率情况。测试用例的优先级排序中,用例的缺陷检测能力往往是一个衡量测试执行效率的重要标准,大量研究[10-11]中也通过观察测试执行的失效情况来评判测试用例的缺陷检测能力。而实际测试过程中,测试人员通常需要根据需求分析或概要设计来分辨测试用例在此次测试执行过程中的重要程度。为了尽快满足可变力度的组合覆盖要求和缺陷的检测能力,实现SUT设计文档的需求,本文引入局部组合覆盖率、测试用例失效率和测试用例重要程度这3个排序因素确定可变力度的组合测试用例的优先级问题。 1)局部组合覆盖率(Locally-Interaction-Coverage Rate,LICR),局部组合覆盖率是当前时刻下测试用例在局部影响因子集中覆盖所有λ元组合,且这些λ元组合尚未被测试用例序列覆盖的概率。 LICR(λ,ti,F′)(tc,Sti-1)= (1) 其中:CombSet(λ,F′)(tc)是测试用例tc在F′中覆盖所有λ元组合的集合,UncovCombSet(λ,F′)(Sti-1)是测试用例序列Sti-1在F′中未覆盖所有λ元组合的集合,n为F′中影响因子的个数。当F′=F时,局部组合覆盖率LICR(λ,ti,F′)(tc,Sti-1)即为测试用例tc在ti时刻的λ元组合覆盖率。 为了便于对局部组合覆盖率的理解,给出图1所示的计算实例。当前存在5个影响因子F={f1,f2,f3,f4,f5},每个因素分别有两种取值。St3中已经执行了三个测试用例,Tt3中余下测试用例tc1和tc2。t4时刻,λ=2时,局部影响因子集F′={f1,f3,f4,f5}分别计算LICR(2,t4,F′)(tc1,St3)和LICR(2,t4,F′)(tc2,St3)。 图1 局部组合覆盖率计算实例 2)测试用例失效率(test case failure rate,FR),测试用例失效率是当前时刻下测试用例局部影响因子集F′中所有影响因子对应参数取值失效率的平均值。参数取值失效率FR(tc,ti,F′)(fk,p)是ti时刻测试用例tc在影响因子集F′中,fk对应取值为p的失效率。用m(tc,ti,F′)表示取值失效个数,即测试用例tc在局部影响因子集F′中,ti时刻参数取值失效率不为0的参数取值个数,即FR(tc,ti,F′)(fk,p)≠0的参数取值个数。那么ti时刻下,测试用例失效率FR(tc,ti,F′)计算公式如下: (2) 其中:fk∈F′,∑FR(tc,ti,F′)(fk,p)是计算局部影响因子集F′中所有fk对应取值为p失效率之和。 表1 某组合空间配置在ti-1时刻参数取值失效率的情况 测试过程中,测试用例序列和测试用例集中测试用例的个数不断发生变化,使得局部组合覆盖率也不断发生变化。优先执行局部组合覆盖率较大的测试用例,能够保证尽快满足组合覆盖率的要求。若ti-1(i≥1)时刻所选取的测试用例为Ati-1,那么在该测试用例执行测试后,测试用例序列Sti-1和测试用例集Tti-1都发生了改变,进而得到每个测试用例在当前时刻下的覆盖组合集CombSet和未覆盖组合集UncovCombSet,并为下一次求解局部组合覆盖率做准备。 其中,ti时刻的测试用例序列Sti以ti-1时刻执行的测试用例Ati-1顺序插入到ti-1时刻的测试序列Sti-1的形式表示,如公式(3)所示。 Sti=Sti-1≻Ati-1,Ati-1∈Tti-1 (3) ti时刻的测试用例集Tti通过测试用例Ati-1从ti-1时刻的测试用例集Tti-1中移除得到,如公式(4)所示。 Tti=Tti-1-Ati-1,Ati-1∈Tti-1 (4) ti时刻,未覆盖λ元组合集UncovCombSet(λ,F′)(Sti)是通过移除测试用例Ati-1在ti-1时刻覆盖了测试用例序列Sti尚未覆盖的λ元组合集而得,如公式(5)所示。 UncovCombSet(λ,F′)(Sti)=UncovCombSet(λ,F′)(Sti-1)- (UncovCombSet(λ,F′)(Sti-1)∩CombSet(λ,F′)(Ati-1)), Ati-1∈Tti-1 (5) 每执行一个测试用例,都需要对当前测试用例序列、测试用例集和每个测试用例的局部组合覆盖率了进行更新,执行完测试用例Ati-1后,每个测试用例的局部组合覆盖率的计算公式如(6)所示。 LICR(λ,ti,F′)(tc,Sti)= (6) 实际测试中,当前测试用例的执行结果能够反馈出SUT存在的问题。研究表明,相同组合影响因子的参数取值引起的失效,可能隐藏了更多的错误,并且可以会检测出相同或者类似的错误[12-13]。测试用例的执行能够发现存在的错误与缺陷,那么测试用例在当前选取的局部影响因子集F′中所覆盖的参数取值的失效率需要做出相应的调整,以保证测试用例失效率能够实时计算,确保最终优先级排序的准确性。若ti-1(i≥1)时刻,测试用例Cti-1检测出SUT中存在缺陷,测试结果只能反应软件失效,但无法判断究竟是由哪些参数相互作用引发的失效。因此,只能对Cti-1覆盖部分影响因子集F′中所有参数取值的失效率相应增加,其他参数取值的失效率保持不变。则ti时刻,各参数取值失效率可用以下公式进行调整: (7) 其中:Δc是一个较小的常量。 若ti-1时刻,测试用例Cti-1未检测出SUT中存在缺陷,测试结果能够反应出当前测试用例中所有参数取值不会对SUT造成缺陷,则该测试用例覆盖局部影响因子集F′中所有参数取值的失效率变为0,其他参数取值的失效率保持不变。则ti时刻,各参数取值失效率可用以下公式进行调整: (8) 为了便于对局部影响因子集F′中参数取值失效率在线调整的过程,通过以下示例对其做出解释。参数取值失效率情况见表1。若当前测试用例tc={5,1,2,8,4}在ti-1时刻检测出SUT中存在缺陷,测试时对应的局部影响因子集F′={f1,f3,f4,f5},此时需要对测试用例tc覆盖部分影响因子集F′中所有参数取值的失效率相应增加Δc,故这个组合空间配置参加取值失效率发生变化,则ti时刻参数取值失效率的情况如表2;同理,若tc未检测出缺陷,相应参数取值失效率变为0即可。 表2 某组合空间配置在ti时刻的参数取值失效率情况 在组合测试过程中,由于OTT策略高效、简单、便于扩展等特点[14],使得该策略在组合测试中得到了广泛的应用,其在组合测试用例优先级排序中的作用也不容忽视。张娜等人[15]在固定力度组合测试用例优先级排序算法中,结合了OTT策略,使得排序后的测试用例具有更强的缺陷检测能力。为此,有必要进一步对OTT策略在可变力度的组合测试用例优先级排序中的应用进行研究。Cohen等人[16]在组合测试的研究中,利用OTT策略构建了Greedy算法的框架。该策略为一维扩展机制,本文结合该策略构建了可变力度组合测试用例优先级排序的算法框架,即每次选取当前优先级最高的测试用例用于执行。本文OTT策略的可变力度组合测试用例优先级排序算法框架流程图见图2。 图2 OTT策略基本算法框架流程图 随着软件版本更新升级速度的提升,对测试效率的要求也随之增高。由于资源时间等的限制,目前的情形无法达到完全测试的目标,那么如何选取测试用例用于执行、测试用例的执行顺序显得尤为重要。本文结合OTT策略将可变力度的组合测试用例优先级排序方法转换成综合考虑多个优先级排序影响因素共同计算优先级、每次选取当前优先级最高的用例用于执行的问题。为了尽快满足可变力度组合测试在不同影响因子集下的组合覆盖率,尽可能选取局部组合覆盖率较高的测试用例;同时,提高缺陷检测的能力,要求优先考虑测试用例失效率较高的测试用例;并且,测试用例的设计和生成过程中,本身存在一定的优先级,测试人员可结合需求设计文档或凭借测试经验,给组合测试用例赋予一定的重要程度。那么,不同参数取值的重要程度本身存在差异,使用参数取值重要程度的加权平均值作为测试用例重要程度的计算。根据OTT策略基本算法框架扩展组合测试用例优先级排序算法,每次选择出当前优先级最高的测试用例。测试用例重要程度I(tc,F′)是测试用例tc的重要程度,即测试用例在局部影响因子集F′所有影响因子对应取值权重的平均值。参数取值重要程度ω(fk,p)是影响因子fk中,取值为p的重要程度。 那么,测试用例tc在ti时刻的优先级Pr由测试用例的局部组合覆盖率、测试用例失效率和测试用例重要程度这三个排序因素共同决定,并利用权重因子,以便不同测试环境下对这三个排序因素比重做出相应调整,保证该方法能够广泛的用于软件测试中。优先级计算方法如下所示: Pr(tc,ti)=α·LICR(λ,ti,F′)(tc,Sti-1)+ β·FR(tc,ti,F′)+γ·I(tc,F′) (9) 其中:α、β、γ分别表示局部组合覆盖率、测试用例失效率和测试用例重要程度的权重因子,实际测试过程中可根据具体情况相应调整,只有保证α+β+γ=1即可。测试用例的重要程度使用每个参数取值重要程度的平均值进行计算。通过上述公式的描述,测试用例tc在ti时刻的优先级Pr(tc,ti)实际可以表示成如下形式: Pr(tc,ti)= (10) 其中:fk∈F′,n为F′中影响因子的个数,∑ω(fk,p)是计算计算局部影响因子集F′中所有fk对应取值为p重要程度之和。 测试用例tc在ti时刻优先级Pr计算过程中,还应当考虑当前影响因子集如何选取的问题,此问题是可变力度的组合测试用例优先级计算时必须着重讨论的。ti时刻,当所有λm元组合还未被测试用例序列Sti-1所覆盖时,考虑影响因子集F上λm元的组合覆盖率;若此时所有λm元组合均被测试用例序列Sti-1所覆盖,则不再考虑影响因子集F上λs元组合覆盖情况,而是仅考虑影响因子集F′上λs元的组合覆盖率。 基于OTT策略的可变力度组合测试用例优先级排序算法(Variable Combinatorial Test Case Prioritization Based Strategy of One-test-at-a-time,VCPO)如下所示。 算法1:VCPO算法。 输入:初始测试用例集Tt0,组合测试覆盖表VSCA(N,λm,n,F,CA(N′,λs,n′,F′))。 输出:测试用例序列Sti。 1)St0=φ;i=0; 2)while |Sti|≠Ndo//未达到测试目标 3)highest=0; 4)TestCase=φ;//当前优先级最高的测试用例集 5)R=F;λ=λm; 6)for each elemente∈(Tti\Sti)do //e在(初始)候选测试用例集Tti中,但不在测试用例序列Sti中 7)ifR==F&&λ==λm&&UncovCombSet(λ,R)(St)≠φ //根据测试用例序列Sti中覆盖组合情况,选择影响因子集和测试力度 8)R=F;λ=λm; 9)else 10)R=F′;λ=λs; 11)priority=α·LICR(λ,ti+1,R)(e,Sti)+β·FR(e,ti+1,R)+γ·I(e,R); 12)ifpriority≥highestthen 13)TestCase=φ; 14)highest=priority; 15)TestCase=TestCase∪{e}; 16)end if 17)end for 18)tc=random(TestCase); //在TestCase随机选取一个测试用例 19)执行测试用例tc; 20)iftcis false then //测试用例检测出缺陷,按照公式(7)调整失效率 21)for each elementfk∈Rdo 22)for each elementp∈fkdo 23)ifp∈tcthen FR(tc,ti+1,R)(fk,p)=FR(tc,ti,R)(fk,p)+Δc; 24)elseFR(tc,ti+1,R)(fk,p)=FR(tc,ti,R)(fk,p); 25)end for 26)end for 27)else //测试用例未检测出缺陷,按照公式(8)调整失效率 28)for each elementfk∈Rdo 29)for each elementp∈fkdo 30)ifp∈tcthenFR(tc,ti+1,R)(fk,p)=0; 31)elseFR(tc,ti+1,R)(fk,p)=FR(tc,ti,R)(fk,p); 32)end for 33)end for 34)i++; 35)Sti=Sti-1≻{tc}; //将测试用例tc有序插入到测试用例序列S中 36)Tti=Tti-1-{tc}; //将测试用例tc从测试用例集T中删除 37)UncovCombSet(λ,R)(Sti)=UncovCombSet(λ,R)(Sti-1)-(UncovCombSet(λ,R)(Sti-1)∩CombSet(λ,R)(tc)); 38)end while 39)returnSti; 为了验证所述方法的有效性,选取以下两个组合空间配置VSCA1(N,λm,8,435362,CA(N′,λs,7,435361))和VSCA2(N,λm,9,1019181716151413121,CA(N′,λs,5,6151413121)),分别采用Random、ICBP、GISVSP、LISVSP和本文所述方法对其缺陷检测能力进行比较。由于实际测试过程中,无法执行组合测试用例集里所有的测试用例,且组合测试用例集不能检测出SUT中所有的缺陷,故缺陷检测能力采用文献[17]提出的标准化的测试用例序列度量标准(NAPFD)。VSCA1和VSCA2在ACTS工具下生成的测试用例情况如表3。 表3 ACTS生成的可变力度组合测试用例集大小 对于上述方法及组合空间配置的情况,为取得适合本文组合空间配置的权重因子α、β、γ,多次实验以调整优先级。并且在测试过程中,每组权重因子下,分别多次模拟测试,记录每次测试的运行结果,用于计算上述方法的NAPFD值。实验对比后,本文对α、β、γ的取值分别为0.41、0.35、0.24,且对比每种方法在实验中NAPFD的最大值和平均值。测试过程中某个测试用例发现缺陷时,则该测试用例覆盖影响因子集中的所有参数取值失效率需相应增加Δc,实验中Δc的取值为0.1。ICBP方法是固定力度组合测试用例优先级排序方法,则选取不同组合力度,以观察力度选取的影响。实验结果如表4。 上述表中,ICBP-λ=n为ICBP方法在测试时,选择组合力度为n的情况;下划线、加粗为每行中最大值;下划线、斜体为每行中次最大值;“-”为不存在的情况,无实验数据。 从表中描述的所有实验结果的Max和Avg可以看到,Random、ICBP方法,在可变力度组合测试的缺陷检测能力上几乎无任何优势。可变力度的组合测试用例优先级排序方法中,GISVSP方法相较于LISVSP方法有更高的最大值;VCPO方法则在最大值和平均值上都占有一定优势,且在每行的最大值和次最大值中都能够有较高的NAPFD值,因此缺陷检测能力相对较高。 因此可得到如下结论: 1)Random和固定力度组合测试优先级排序方法ICBP在可变力度组合测试优先级排序中不适用,原因在于无法选取合适的组合力度用于测试; 2)可变力度的组合测试用例优先级排序方法中,GISVSP方法和LISVSP方法不会面临组合力度选取困难的问题,能够适用于可变力度的组合测试优先级的排序,但其仅考虑组合覆盖率的情况,排序因素单一,故缺陷检测能力没有表现为最优。 3)可变力度的组合测试用例优先级排序方法中,VCPO方法能够解决组合力度选取的难题和排序因素单一的问题,使得排序结果相对稳定。实验结果表明,该方法在大多数情况下缺陷检测能力比其它排序方法更优。 目前组合测试领域中,因实际测试中各影响因子间相对复杂的交互关系,可变力度的组合测试备受青睐,众多研究者关注于可变力度的组合测试用例优先级排序的问题。本文提出了一种基于OTT策略的可变力度组合测试用例优先级排序方法,该方法能够更为广泛的适用于可变力度的组合测试中,且结合了多个排序因素,利用在线的测试反馈信息,在符合实际的测试过程的前提下,进一步提升了缺陷检测能力。 由于测试过程中,本文提出的方法存在不够理想的实验结果,且α、β、γ的权重比值需人为分配,实验中Δc的取值相对固定,后期希望能够选取更合适的排序因素且结合自适应的方法进行在线调整权重因子和Δc的取值。 表4 五种优先级排序算法在不同组合空间配置下的NAPFD(%)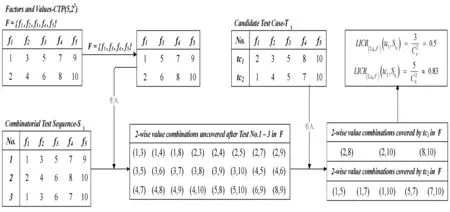

2 优先级排序因素在线调整策略
2.1 局部组合覆盖率调整方法设计
2.2 测试用例失效率调整方法设计

3 组合测试用例优先级排序方法分析
3.1 OTT基本算法框架

3.2 优先级排序方法设计
4 实验与总计
4.1 实验数据与结果分析

4.2 总结