考虑热特性的双丝杠进给系统同步误差实验与分析*
韩 兴,胡小秋,周义成
(1.南京理工大学 机械工程学院,南京 210094;2.工信部高端装备制造技术协调创新中心, 南京 210094)
0 引言
双丝杠驱动进给系统具有良好的动态特性,且负载大,响应速度快,多应用于大型、高速、高精度加工中心。双丝杠所受载荷不同引起的热变形不一致,是影响双驱进给系统同步误差的重要原因。
Ivan[1],Min[2]考虑了丝杠刚度、阻尼,通过Lagrange方程建立了龙门机床同步误差模型。程瑶等[3-5]利用Laplace变换,对同步误差模型解耦,并通过实验加以验证。谢黎明等[6]通过仿真分析了重心位置变化对同步误差的影响。韩军[7-8],陈诚[9]分析了丝杠热变形及热平衡时间。刘兴业等[10]分析了进给系统不同位置的温度场及热变形。目前的研究多集中于单丝杠热分析,对于双驱进给系统的热分析很少见。
本文以卧式加工中心为研究对象,通过理论分析与有限元仿真得出进给系统温度场和同步误差。通过实验测得丝杠各点温度以及工作台偏转角,分析进给速度对丝杠发热量及同步误差的影响。
1 双驱进给系统温度场模型
1.1 进给系统温度场微分方程
对于封闭热力系统,进入的能量与流出的能量以及封闭系统的总能量之间的关系如下:
Q=ΔU-ΔEk+ΔEp+W
(1)
式中,Q—热力系统吸收的能量;W—热力系统对外做功;ΔU—热力系统的内能;ΔEK—热力系统的动能;ΔEp—热力系统的势能。
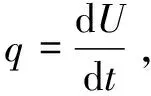
(2)
(3)
式中,q—热流密度,W/m2;nx,ny,nz—等温面在直角坐标系中的分量;t—物体温度;λ—导热系数,W/m·℃;gradt—温度梯度。
将丝杠等效为圆柱体,没有内热源,则丝杠热传导微分方程为:
(4)
式中,α—热扩散率,m2/s;ρ—密度,kg/m3,c—热容,J/(kg·K)。
1.2 进给系统发热量计算
1.2.1 轴承生热模型
滚动轴承的摩擦生热对进给系统的热特性影响较大,轴承摩擦生热主要由轴承摩擦力矩及润滑剂黏性摩擦引起的。
Q1=1.047×10-4n·M
(5)
式中,n—轴承转速,r/min;M—轴承摩擦力矩,N·mm。
M=M0+M1
(6)
式中,M0—粘性润滑剂产生的摩擦力矩;M1—负载产生的摩擦力矩,N·mm;f0—与润滑方式有关的系数;v—润滑剂运动粘度;dm—轴承平均直径,mm;P1—轴承负荷,N。
1.2.2 丝杠螺母生热模型
滚珠丝杠发热主要与负载产生的摩擦力矩和预紧力矩有关。
Q2=0.12πnM
(7)
式中,Q2—丝杠螺母单位时间内的发热量,kJ/h;n—丝杠转速,r/min;M—丝杠螺母副的总摩擦力矩,Nm。

(8)
式中,MD—负载(切削力和摩擦力)力矩;Mpl—预紧力矩,N·m;F—当量轴向载荷,N;Fp—丝杠螺母预紧力,N;L—丝杠导程;η—滚珠丝杠副工作效率。
1.2.3 滚珠丝杠对流换热系数
滚珠丝杠旋转时,丝杠与空气之间为强迫对流换热,对流换热系数为:

(9)
式中,h—对流换热系数;Re—雷诺数;Pr—普朗特数;Nu—怒谢尔特数;ω—角速度,rad/s;v1—空气运动粘度,m2/s;d—丝杠直径,m;λ—空气导热系数,W/m·K。
2 进给系统热变形分析
以卧式加工中心Z向进给系统为例,通过1节中的公式,计算出工作台以不同的速度进给,主、从动轴热流密度q1、q2,轴承热流密度q3,以及丝杠对流换热系数h,如表1所示。
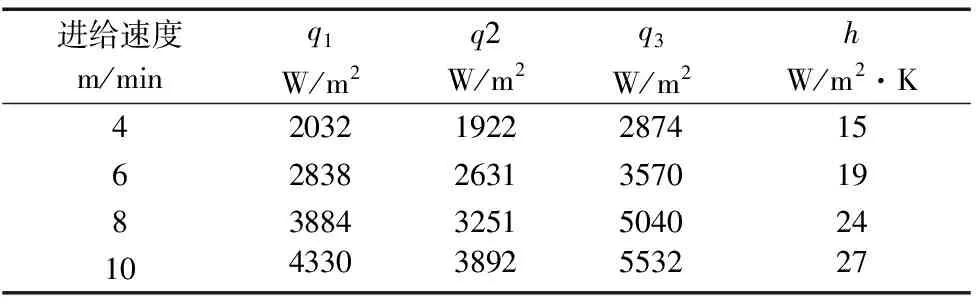
表1 热—结构分析边界条件
图1、图2为工作台以4m/min匀速运行时,进给系统的温度场和热变形云图。轴承1、2的热平衡温度分别为36.2℃和34.1℃,丝杠螺母1、2的温度热平衡温度分别为32.5℃和 32.2℃。由于螺母主要与工作台接触传热,工作台换热面积大,而轴承主要通过轴承座散热,散热面积小,且与床身没有相对运动,因此轴承的热平衡温度明显高于螺母的热平衡温度。主动轴与从动轴的丝杠螺母副的温度差异而产生的热变形,使工作台偏转。如图2所示,主、从动轴螺母热变形分别为δ1=4.60μm,δ2=1.13μm同步误差为δ为δ1-δ2=3.47μm。

图1 进给系统温度场 图2 进给系统热变形
3 实验验证
3.1 实验设备
利用Renishaw XL激光干涉仪测量工作台几何误差、同步误差;磁吸式热电阻温度传感器PT100测量轴承座、螺母温度;温度巡检仪采集机床运行时丝杠的温度,如图3所示。

图3 实验装置
3.2 实验方案
为了验证理论计算与有限元分析的准确性,工作台分别以4m/min、6m/min,8m/min,10m/min速度进给,同时测量丝杠、螺母、轴承座的温度及工作台同步误差。如图4所示,进给系统有效长度为600mm,将其分为12个测量点,前后轴承座各放置一个测量点。在不同速度下,工作台往复运动5次取测量平均值,提高测量精度。

图4 测点布置
3.3 温度场测量与分析
工作台以8m/min进给时,主动轴个点温度如图5。前轴承座由于散热面积小,其温度明显高于后轴承座,因此丝杠上距离前轴承座越近的测温点,其热平衡温度越高,但热平衡时间基本一致,约为60min。
主动轴所受负载大,其轴承、丝杠螺母的发热量较大。如图6、图7所示,不同进给速度下,主、从动轴温度变化趋势相同,但主动轴各测点温度明显高于从动轴。进给速度为8m/min时,热平衡后,主动轴丝杠测点温度比从动轴高1℃~2℃,主动轴螺母测点(P12)温度为36.8℃,比从动轴高2.8℃。
温度与进给速度呈非线性关系,60min之前,进给速度越快,螺母温度变化率越大,热平衡温度越高。速度为4m/min时,丝杠螺母温度变化小,主要原因是进给速度低,丝杠螺母发热量少,且单位时间内处于对流换热状态的丝杆面积较大。工作台以10m/min进给时,螺母往复运动频率高,发热量大,热平衡温度有明显上升。
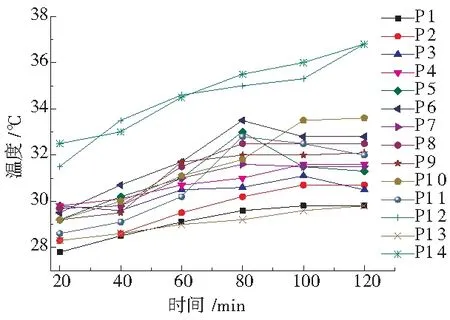
P1~P11:丝杠测温点 P12:螺母测温点 P13:后轴承座测温点 P14:前轴承座测温点图5 主动轴各测点温度
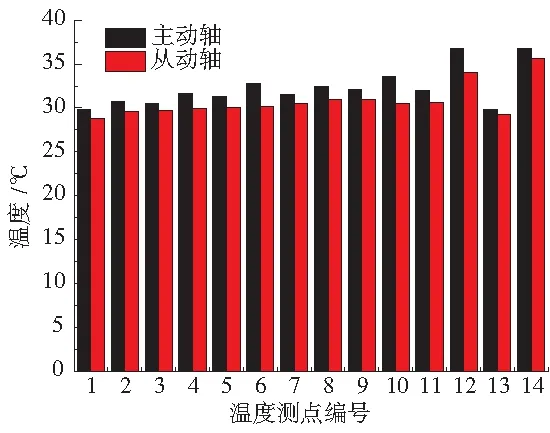
图6主、从动轴热平衡后温度
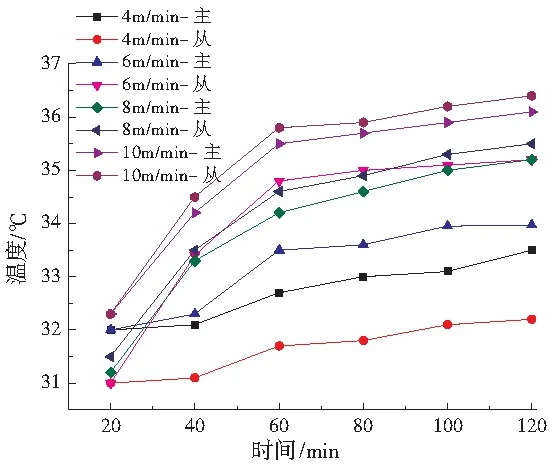
图7 主、从动轴螺母温度变化曲线
3.4 同步误差分析
利用激光干涉仪测量工作台运动过程中扭转角θ,见图8。当θ较小时,同步误差Δy=Lsinθ≈Lθ,其中L为双丝杠间距。热平衡后,测得Δy的减去冷态下测量的几何误差(表2),即为进给系统的同步误差。

图8 同步误差测量原理
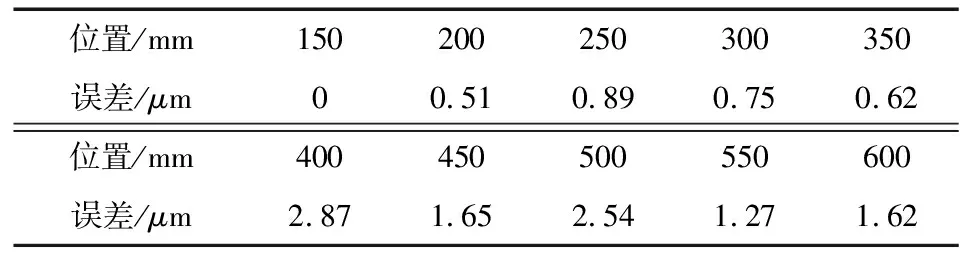
表2 冷态几何误差
滚珠丝杠副采用固定—固定预拉伸的安装方式。一般情况下,丝杠的热变形不会超过预拉伸量,即丝杠两端固定,丝杠不能因热变形成弯曲状态。由图9可知,同步误差随着进给时间、进给速度的增加而增加,热平衡后,同步误差波动范围很小,其变化趋势与丝杠螺母的温度变化趋势相同。
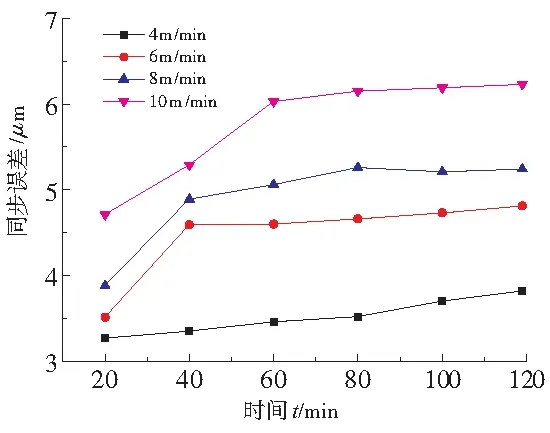
图9 同步误差变化曲线
取热平衡后各进给速度下同步误差的平均值如表3,实验结果与有限元仿真结果误差在15%以内,主要原因是丝杠的实际变形量为预拉伸量ΔL1,2与热变形δ1,2之差,则同步误差可表示为Δy=(ΔL1-δ1)-(ΔL2-δ2),即双丝杠预拉伸量ΔL1,ΔL2、的差异对同步误差有一定影响。进给速度为10m/min时误差最大,最要原因是丝杠螺母的热膨胀产生的轴向力减小了丝杠的预紧力,降低了丝杠轴向刚度,双丝杠轴向刚度的差异进一步增大了同步误差。

表3 同步误差实验与仿真数据对比
4 结论
通过对双丝杠进给系统的温度场和同步误差的测量,以及有限元分析结果,最终结论如下:
(1)丝杠的温升使丝杠产生热膨胀,降低丝杠-螺母副轴向刚度。双丝杠温度差异使得双丝杠的热变形量和轴向刚度变化量不同,进而产生同步误差,而有限元仿真中只有温度对热变形的影响,没有考虑轴向刚度随温度的变化,因此,进给速度为10m/min时,仿真值与实验值有较大误差。
(2)同步误差与时间成非线性关系,与丝杠温度变化趋势相同。丝杠温度在60min左右达到热平衡状态,同步误差约在80min达到稳态,这表明同步误差相对于丝杠温度的变化具有时间滞后性。
(3)由于导轨摩擦力、丝杠螺母预紧力的不同以及工件装夹位置、切削力等因素,双丝杠负载无法完全相同,因此双丝杠载荷差异较大时,应降低进给速度,减小同步误差。

