基于SVD-PE的高速列车滚动轴承故障诊断模型*

冯 波

(四川交通职业技术学院，成都 611130)

0 引言

滚动轴承是旋转机械系统最重要的组成部件之一[1]，其发生故障将对旋转机械系统造成不可估量的损失，轻则导致系统损坏造成经济损失，重则可能导致人员伤亡等意外事故。而滚动轴承作为高速列车最重要的工作部件，其发生故障可导致轮毂抱死甚至脱轨等重大安全事件[2]。因此，滚动轴承能否安全可靠地运行将对高速列车乃至机械系统具有重要的意义。

目前滚动轴承故障诊断存在诊断率不高，信号降噪效果不理想等缺点[3]，因此，采用科学有效的方法对滚动轴承振动信号进行准确诊断，最终达到轴承故障准确判别显得尤为重要。早期滚动轴承声学信号具有噪声大、信噪比低的特点，Tian Y等[4]通过局部均值分解与奇异值分解方法对滚动轴承声学信号进行特征提取，然后再输入极端学习机[5](Extreme Learning Machine, ELM)进行故障分类,该方法虽达到了预期的效果，但在局部均值分解过程因端点效应产生的PF分量存在虚假分量，故容易对故障分类造成误判; 郑近德等[6]在解决EMD分解过程中固有模态函数(IMF)的判据和端点效应问题后利用希尔伯特变换(HHT)对故障轴承进行方法研究，但EMD分解求取包络函数过程中因过冲和欠冲的问题，分解产生的IMF分量相邻极值点间存在零交叉点，这样对后续的分析结果造成了影响。

针对高速列车滚动轴承故障信号具有噪声大、信噪比低的特点，本文运用奇异值分解(SVD)与排列熵(PE)方法相结合对高速列车滚动轴承故障信号进行处理，SVD可将高速列车滚子轴承故障信号经过选取合适的奇异值后进行重组，从而滤除噪声信号以达到对信号降噪的目的，提高了信号的信噪比，此外，PE通过熵值的变化可将信号从动力学角度分析滚动轴承信号特点，并结合支持向量机分类速度快、效率高的优势对故障类型进行判别，最终达到滚动轴承故障诊断的目的。

1 奇异值分解(SVD)理论

奇异值分解(Singular Value Decomposition, SVD)是一种非线性滤波降噪方法[7]，它在旋转机械等工程实际中已经得到广泛应用。SVD的工作原理是将原始信号矩阵分解为左奇异、右奇异和奇异值分布三个向量，其中奇异值分布向量中奇异值的大小代表了其在原始信号中的比重[8]，故选择合适奇异值降噪阶次并进行重构可以实现去除噪声干扰信号，这种方法可以有效地避免了传统信号滤波方法难以滤除频带中混叠噪声干扰信号的问题。具体处理步骤如下：

首先利用采样后的离散时间信号X={X0,X1,…,XN-1)}，构造m×n维(m≥n)吸引子轨迹矩阵A，则Am×n可表示为：

(1)

其中，m+n-1=N；首先，对Am×n奇异值分解得到左奇异U、右奇异V和奇异值Λ分布三个矩阵：

A=UΛVT

(2)

式中，左奇异U和右奇异V分别是m×m型和n×n型正交阵，奇异值分布Λ矩阵表示为：

(3)

其中，Σ=diag[σ1σ2…σr]，r=rankA。σi为矩阵A的奇异值(i=1,2,…,r)，并满足σ1≥σ2≥…σr≥0。

当信号长度N一定时，n尽量取较大值，即：

(4)

通过左奇异U和右奇异V两个正交阵的列矢量和奇异值σi，原矩阵A可表示为：

(5)

所以，可通过选取不同的奇异值σi以及它们所对应的各自分量就可以构造出成分不同的信号。故奇异值分解法最重要的两点是构造矩阵A和选取奇异值。首先，本文用Hankel矩阵方式对矩阵A进行构造，待选取合适的奇异值并对信号进行重组。

2 排列熵算法

排列熵(Permutation Entropy, PE)是一种检测时间序列随机性和动力学突变行为的非线性分析方法[9]，它对信号的突变十分敏感。对于滚动轴承故障信号，不同的故障类型其内部的动力学突变行为也不同[10]，故可以依赖PE的敏感特性对故障类型进行特征提取。其具体过程如下：

(1)将长度为n的时间序列X={x(i),i=1,2,…,n}进行相空间重构，即：

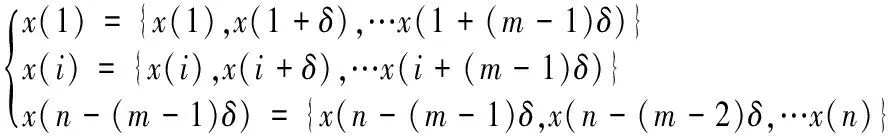
(6)

其中，δ为时延，一般δ取1；m为嵌入维数，m的取值将直接影响排列熵的大小，一般m取3～7。

(2)将时间序列x(i)进行升序排列，即：

x(i)={x(i-(k1-1)δ≤

x(i-(k2-1)δ)≤…≤x(i+(km-1)δ)}

(7)

得到符号序列L(g)={k1,k2,…,km}。

(3)计算每种符号序列出现的概率Pn，其中P1,P2,…Pk,k∈n是每一种符号序列出现的概率。

(4)计算排列熵值

(8)

式中，0≤Hp(m)≤ln(m!),当Pj=1/m!时，Hp(m)有最大值ln(m)。通常，对Hp(m)进行归一化处理，即：

Hp=Hp(m)/ln(m!)

(9)

上式可以看出0≤Hp≤1。Hp值的大小反映了信号的复杂度和随机程度。Hp值越大信号越随机，反之，则说明信号越规则。Hp值的变化反映和放大了时间序列的局部微小变化。

3 高速列车滚动轴承故障诊断模型构建

首先经奇异值分解对初始信号进行重构，待选取合适的奇异值后再进行信号重组从而达到滤波降噪的目的，然后用排列熵算法对滚动轴承故障信号从动力学角度进行分析，这样一方面可以解决滤波过程误差造成的影响，另外排列熵算法通过熵值的变化有效提取故障信号特征，最后将SVD-PE分析处理结果组成特征向量输入支持向量机进行故障类型判别，故障诊断流程图如图1所示。

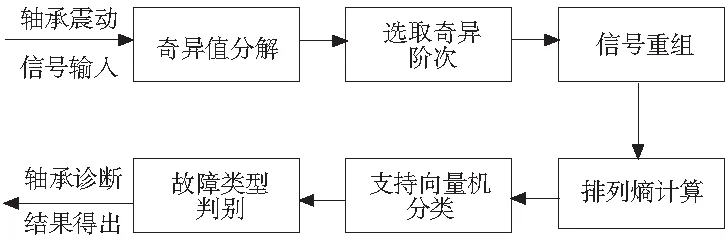
图1 高速列车滚动轴承故障诊断流程

3.1 滚动轴承故障信号故障特征提取

针对高速列车滚动轴承振动信号噪声大、信噪比低的特点，本文首先运用奇异值分解的方法对轴承故障振动信号进行滤波降噪，该信号处理方法是一种非线性滤波降噪方法[11]，它可将滚动轴承振动信号分解成不同阶次的奇异值，而不同的奇异值所对应的信号向量不同，奇异值越大表明其在原信号中所占比例越大，故通过选取合适的奇异值并将其所对应的向量进行重组，即可得到降噪后的信号；新得到的信号较好保留了原始特征信号，但同时也夹杂着轴承运行时产生的调制信号，该类信号具有频段相对集中，传统信号降噪方法难以滤除的特点，这部分信号将对故障类型判别产生影响，故本文通过转换思路，运用排列熵算法从动力学角度分析滚动轴承故障，从而达到轴承故障诊断的目的。具体过程如下：

(1)对滚动轴承振动信号进行Hankel矩阵重构，之后进行奇异值分解，根据分解后的奇异值差分谱选择合适的奇异值，再根据选择的奇异值及其对应的向量进行重组；

(2)对重组后的信号进行排列熵计算，选取m=k,k=3,4,…,7下的排列熵值构成特征向量T=[H3/H,H4/H,…,H7/H]，其中，H为不同嵌入维数下的排列熵之和，即H=∑Hn,n=3,4,…,7这样可有效避免嵌入维数选择不当造成的误差；

(3)将特征向量输入支持向量机进行故障类型判别。

3.2 试验分析

为验证该故障模型的有效性，采用型号为NU2314圆柱滚子轴承，其具体参数：内径为25mm，外径为52mm，节径为34mm，滚子数为13个。

试验采集该型号轴承的内圈、外圈、滚动体三类故障信号，采样频率为51200，轴承转速为600r/min，采样点数为4096。其中，内圈、外圈、滚动体、正常信号的时域图如图2～图5所示。

图2 轴承内圈故障

图3 轴承外圈故障

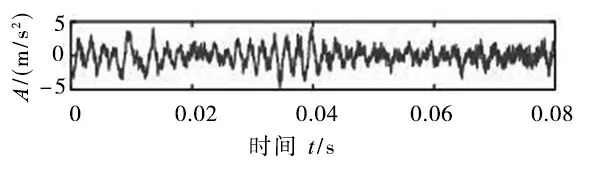
图4 轴承滚动体故障

图5 轴承正常状态

图6 滚动轴承内圈故障

为减少篇幅，现以滚动轴承内圈故障为例进行描述，滚动轴承内圈故障时域图如图6所示。

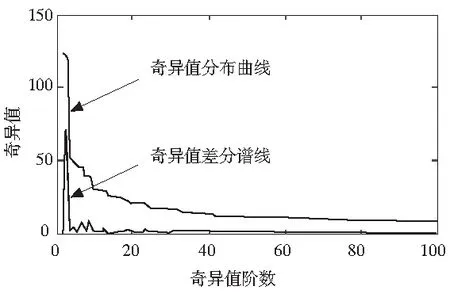
图7 内圈奇异值分布与差分谱曲线

由图6可明显看出内圈故障原始振动信号夹杂着不少强噪声信号，对其进行有效降噪为后续故障诊断具有重要意义，故运用奇异值分解对原始信号进行分解，分解得出的奇异值分布和差分谱曲线如图7所示。

图8 奇异值分解后的信号

根据图7奇异值分布与差分谱曲线选择合适的阶次，并进行信号重组可将轴承内圈信号重构成如图8所示曲线。

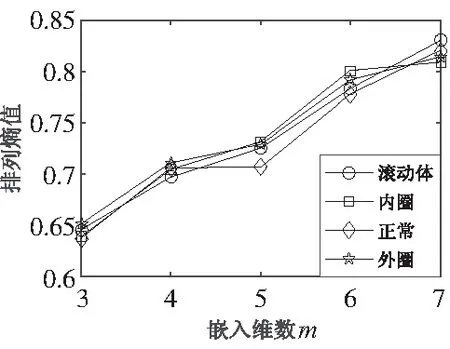
图9 滚动轴承多状态下排列熵

将图6和图8信号曲线进行比较，可清楚看出内圈故障信号经奇异值分解后噪声信号得出有效的滤除，并且保存了原始信号的变化特征。同样，将轴承外圈、滚动体以及正常状态振动信号经奇异值分解，分解重组后的信号再进行排列熵计算，结果如图9所示。

由图9可较明显辨别各状态下滚动轴承信号的排列熵值，但在数据量大的前提下我们无法仅根据排列熵值来辨别故障类型，此外，为了让模型具有自动辨识故障的特点，引入支持向量机[12]

(support vectormachSVM)对故障类型进行辨别。并运用人工神经网络[13](Artificial Neural Networks, ANNs)方法进行比较研究。这里支持向量机分类器采用3个分类器，具体分类流程如图10所示。

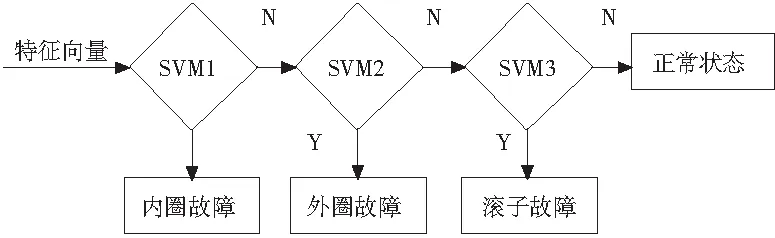
图10 支持向量机分类器分类流程

根据分类器的分类流程，当第一个SVM进行分类时，标记内圈故障为+1，非内圈故障为-1；当第二个SVM进行分类时，标记外圈故障为+1，非外圈故障为-1；第三个SVM进行分类时，标记滚子故障为+1，正常状态为-1，将4种状态(内圈故障、外圈故障、滚动体故障以及正常状态)计算不同嵌入维数下的排列熵值，再对值进行标量量化得到特征向量，然后输入SVM模型分类器进行故障类型判别，最终结果如表1所示。

表1 SVM故障类型分类结果

为充分验证该模型的可行性，现分别对4种状态(内圈故障、外圈故障、滚动体故障以及正常状态)信号取50组数据，总共200组数据，每组4096个点，然后用提出的故障诊断模型方法对信号进行故障类型判别，诊断结果如表2所示。

表2 故障模型诊断结果

由表2统计结果显示，基于SVD-PE的高速列车滚动轴承故障诊断模型的故障识别率可达到90%以上，高于ANNs对滚动轴承故障70%～80%的识别率，故基于SVD-PE的高速列车滚动轴承故障诊断模型具有较高的故障识别率，对滚动轴承故障具有较好的诊断效果，有效证明了该模型的可行性。

4 结束语

针对高速列车滚动轴承振动信号噪声大、信噪比低的特点，提出了首先运用奇异值分解将滚动轴承振动信号进行重组，待根据奇异值差分谱选取合适的奇异值后对信号进行重构，从而完成对噪声的滤除以提高信噪比，此外，本文从动力学角度运用排列熵计算来表征滚动轴承运动过程中其内部力之间的变化，运用熵值的变化来提取故障特征从而间接地获取故障诊断特征，然后利用支持向量机分类效率高、速度快的优势将特征向量输入该模型进行故障类型判别，试验结果表明了该故障诊断模型的有效、可行性。