一类系统谱的上界的不等式

吴 平

(苏州职业大学 数理部，江苏 苏州 215004)

1 问题提出

设Ω⊂Rm是一个逐片光滑的区域，考虑的谱的估计，其中n是边界∂Ω的单位法向量，

(1)

根据相关方程理论知道问题(1)的谱都是正实数且是离散的，离散谱又称特征值。

问题(1)可写成矩阵式，设

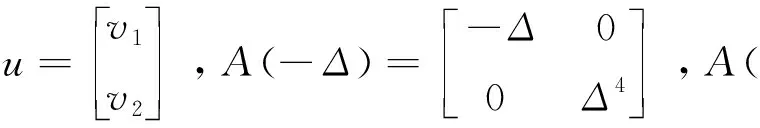
问题(1)可写成矩阵形式

(2)

设问题(2)的谱为：

0≤λ1≤λ2≤···≤λn≤···

对应的正交规范特征向量为u1,u2,···,un,···,即满足：

(3)

利用分部积分，得：

(4)

设：

其中，

显然，φik与uj正交(i,j=1,2,···,n,k=1,2,···,m)，且满足：

于是，根据Rayleigh定理，得到下列不等式：

(5)

计算得：

(6)

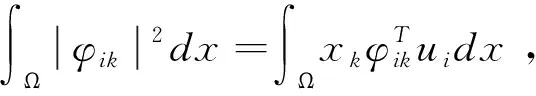
(7)

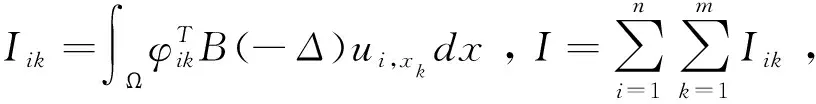
由(7)式，有：

(8)

(9)

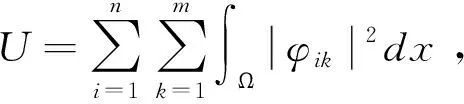
用λn替代(6)式中的λi，则(λn+1-λn)U≤I。

(10)

2主要引理

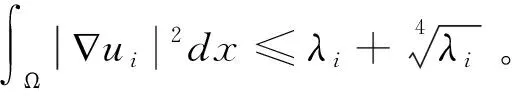
(11)

(12)

同理，

化简，由分部积分法，Schwartz不等式，有：

(13)

由式(11)和式(13)，得：

既得引理1。

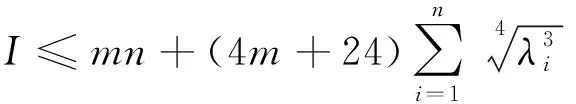
证明 由恒等式和分部积分法，得：

(14)

由(14)式，有：

(15)

由于：

(16)

(17)

(18)

由分部积分，得：

(19)

(20)

由(18)式，(19)式，(20)式和分部积分，有：

即得引理2。

引理3 对于φik和λi(i=1,2,···,n,k=1,2,···,m)，则：

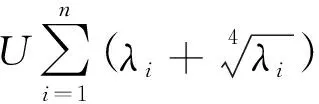
证明 由φik的定义，有：

(21)

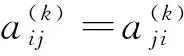
显然：

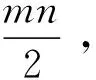
(22)

由Schwartz不等式和引理1，有：

即得引理3

3 主要结论

定理1 如果λi(i=1,2,···,n+1)是问题(3)的谱，则：

23)

(24)

证明 利用引理3，再利用(10)式和引理2，我们可得定理1的(23)式，在(23)式右端用λn替代λi，可得(24)式。

定理2 对于n≥1，则：

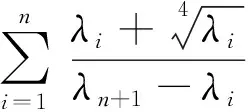
证明 选择参数σ>λn，由(9)式，得：

(25)

利用(22)式和Young不等式，得：

(26)

其中δ>0为待定常数。

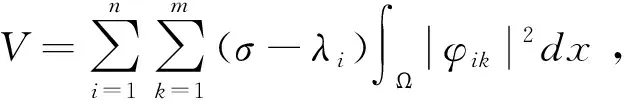
由(25)式，(26)式和引理1，化简得：

(λn+1-σ)U+V≤I，

(27)

(28)

为了使(28)式右端的值达到最小，取

(29)

将(29)式代入(28)式，得：

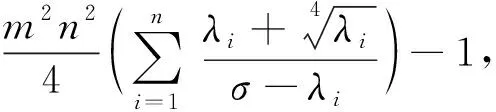
(30)

根据引理2，(27)式和(28)式，得：

(31)

其中σ>λn，选择σ使(31)式右端等于零，即：

(32)

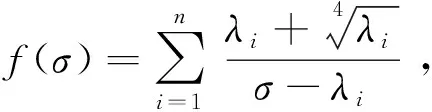
易知，f(σ)是在(λn,+)内单调减少连续函数，其值域为(0,+)，因此，存在唯一的σ使等式(32)成立。从(31)式知σ≥λn+1，用λn+1来替代等式中σ，即得定理2。

4 结语

数学学科研究的一个重要领域就是方程的特征值问题，偏微分方程及偏微分方程组特征值问题的研究就是其中很重要的一个方面。本文所研究的问题就属于这一方面的内容，文中采用了分部积分、Rayleigh定理以及不等式估计等数学方法，得到了问题(1)的谱的上界的不等式。其结果应用广泛，特别在物理学和力学等领域。