基于灰色关联综合评价的高职专业评估研究

郑承志

(黎明职业大学 经济管理学院，福建 泉州 362000)

1 高职专业评估评价指标体系

1.1 高职专业评估评价指标

目前，已有少量关于高职及普通高校专业评估评价指标设置的文献报道。张丽萍等从专业定位、专业办学条件、专业教学管理以及专业教学效果4个方面构建包括15个二级指标的高职专业评估两级评价指标体系[1]；王珑从专业设置、专业实力以及服务能力3个方面构建包括17个二级指标的两级评价指标体系[2]；陈晓云等从专业规划与培养模式、课程建设、实践教学、教学团队、教学管理、人才质量、特色与创新、社会服务8个方面构建包括27个二级指标的两级评价指标体系[3]；彭振宇从培养方案、教学管理、师资团队、教学条件、培养质量以及社会服务能力6个方面构建包括30个二级指标的两级评价指标体系[4]；万德年从专业团队、课程建设与教学、教学保障、人才培养质量与社会服务4个方面构建包括20个二级指标的两级评价指标体系[5]；罗美玲从专业建设目标、建设资源配置、建设运行实施以及建设绩效4个方面构建包括12个二级指标的两级评价指标体系[6]。

上述研究报道中，文献[1]和[6]的指标设置过于简化，文献[2]的一级指标太少，导致个别一级指标下的二级指标比较杂乱，而文献[3]的一级指标则偏多。另外，所有这些研究报道中都没有质量提升工程方面的指标，多数文献在企业一线兼职教师队伍建设、校企合作实训基地建设等方面也考虑不足。克服这些不足并充分考虑高职教育的特点，本文构建了高职专业评估指标体系，如表1所示。

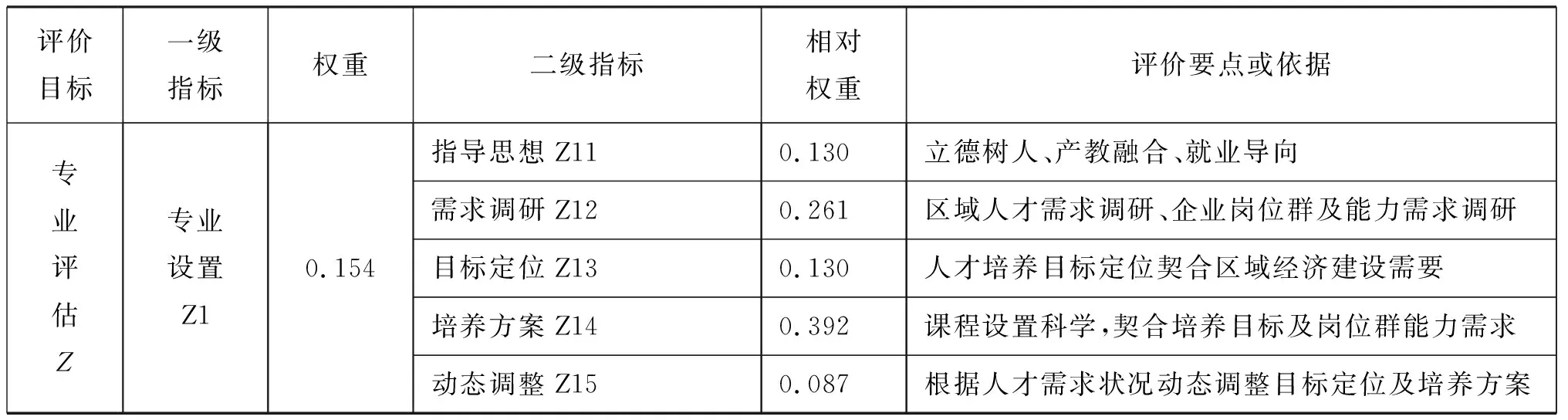
表1 高职专业评估指标体系

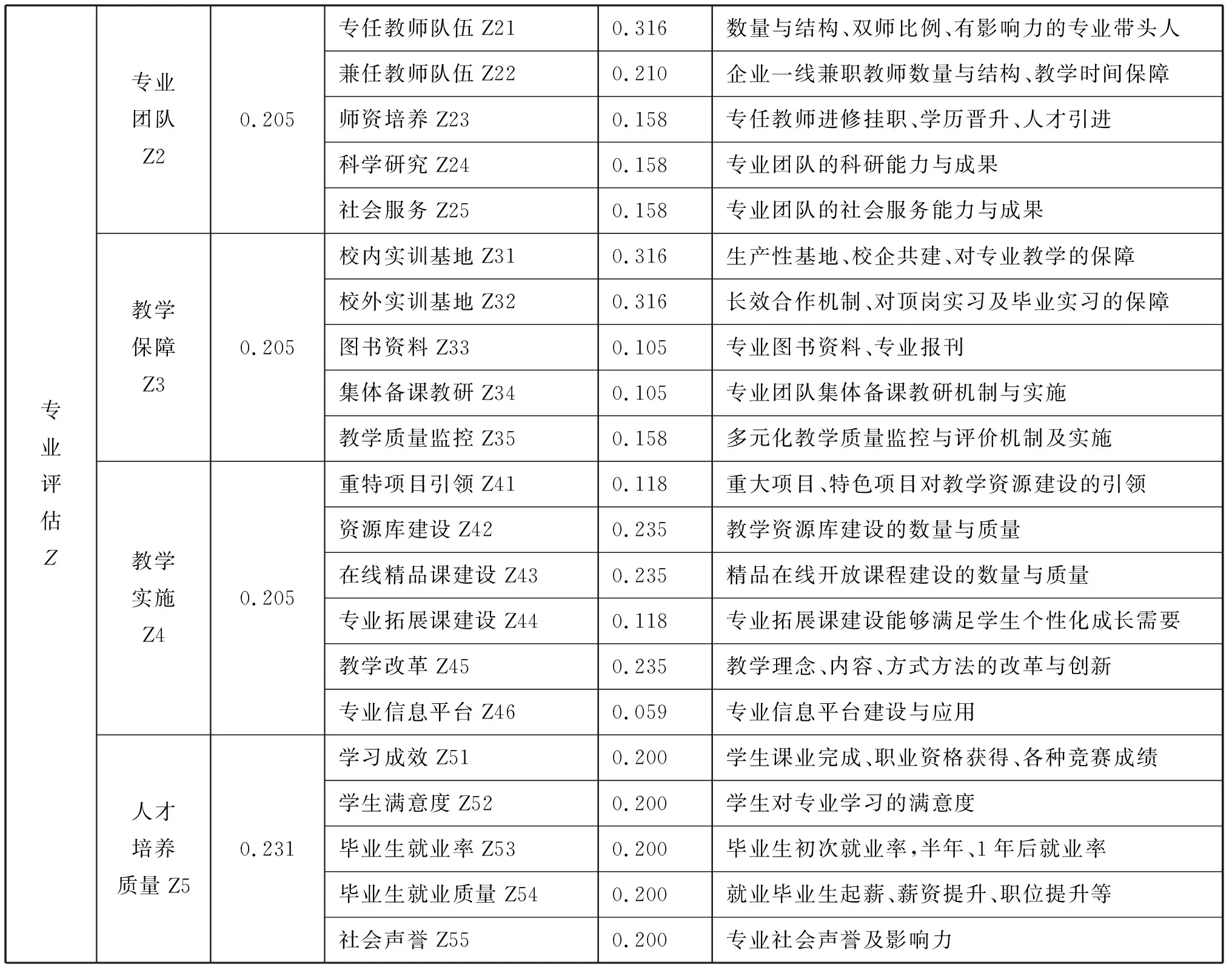
专业评估Z专业团队Z2教学保障Z3教学实施Z4人才培养质量Z50.2050.2050.2050.231专任教师队伍Z21兼任教师队伍Z22师资培养Z23科学研究Z24社会服务Z25校内实训基地Z31校外实训基地Z32图书资料Z33集体备课教研Z34教学质量监控Z35重特项目引领Z41资源库建设Z42在线精品课建设Z43专业拓展课建设Z44教学改革Z45专业信息平台Z46学习成效Z51学生满意度Z52毕业生就业率Z53毕业生就业质量Z54社会声誉Z550.3160.2100.1580.1580.1580.3160.3160.1050.1050.1580.1180.2350.2350.1180.2350.0590.2000.2000.2000.2000.200数量与结构、双师比例、有影响力的专业带头人企业一线兼职教师数量与结构、教学时间保障专任教师进修挂职、学历晋升、人才引进专业团队的科研能力与成果专业团队的社会服务能力与成果生产性基地、校企共建、对专业教学的保障长效合作机制、对顶岗实习及毕业实习的保障专业图书资料、专业报刊专业团队集体备课教研机制与实施多元化教学质量监控与评价机制及实施重大项目、特色项目对教学资源建设的引领教学资源库建设的数量与质量精品在线开放课程建设的数量与质量专业拓展课建设能够满足学生个性化成长需要教学理念、内容、方式方法的改革与创新专业信息平台建设与应用学生课业完成、职业资格获得、各种竞赛成绩学生对专业学习的满意度毕业生初次就业率,半年、1年后就业率就业毕业生起薪、薪资提升、职位提升等专业社会声誉及影响力

1.2 基于AHP的权重计算

表1所示的指标体系基本上都是定性指标，因此本文采用层次分析法(AHP)计算指标权重。层次分析法是美国学者T. L. Satty提出的一种多准则决策方法，该方法将决策过程层次化、数量化，以此实现定性问题的量化处理[7]。为计算表1指标权重，由3位教学诊断与改进专家在对表1指标体系进行充分讨论的基础上，按照AHP的1-9标度法共同确定表1中一级指标之间以及各一级指标的二级指标之间的相对重要性，以此构建评价目标“专业评估Z”及其一级指标的判断矩阵，然后利用几何平均法计算各判断矩阵所对应(相对)权重向量。例如，一级指标“专业设置Z1”有“指导思想Z11”、“需求调研Z12”、“目标定位Z13”、“培养方案Z14”、“动态调整Z15”5个二级指标，由3位专家一致确定的这5个指标相对重要性比值所构成的相对重要性矩阵为：

此矩阵就是一级指标Z1的判断矩阵。利用几何平均法进行近似计算，该矩阵最大特征值所对应的归一化特征向量为：

此向量也即一级指标Z1的相对权重向量[7]。

对其他4个一级指标以及评价目标可进行类似计算，表1中的权重数据就是计算结果。在计算过程中，所有判断矩阵的随机一致性比率都是0，说明它们具有满意的一致性。

2 高职专业评估多层灰色关联综合评价

对于综合评价问题，参与评判的专家对于评判对象不可能完全了解，即评判对象的信息具有灰性，而信息灰性问题适合采用灰色系统理论加以解决[8]，因此本文采用灰色关联分析法(Grey Relational Analysis，GRA)构建综合评价模型。

2.1 灰色关联综合评价模型

灰色关联分析通过比较各数据序列与参照数据序列的贴近度—关联度—对各数据序列进行排序。假定m个评价对象的n个指标评判值构成的数据序列分别为：

zi={zi(1),zi(2),...,zi(n)}，1≤i≤m

而参照数据序列为：

z0={z0(1),z0(2),...,z0(n)}

那么在各指标数据点zi(1≤i≤m)与z0的灰色关联度(也称为灰色关联系数)为：

(1)

上述灰色关联系数构成m个评价对象的评判矩阵：

(2)

假定评价对象的n个指标的归一化权重向量为：

那么m个评价对象的评价结果向量为：

G=R×W

(3)

此向量的元素是评价对象与最优参照对象的关联系数，根据需要可进一步处理。

2.2 基于灰色关联综合评价高职专业评估示例

某高职二级学院为寻找专业建设中的薄弱环节以便加以改进，特邀请5位校外教学诊断与改进专家对该院5个专业(以下分别以A、B、C、D、E代表这5个专业)进行评估，经院领导与专家组讨论商定采用表1指标体系对专业建设各方面进行综合评价。通过现场考察、资料查阅、专业负责人答辩、教师与学生访谈等环节，专家组成员对5个专业的各底层指标按照10分制进行打分，以5位专家的平均分值作为各专业底层指标的评判值，结果如表2所示。表2同时列出参照数据序列，该系列各数据点的值取5个专业评判值最大者，这也是灰色关联分析的典型做法。

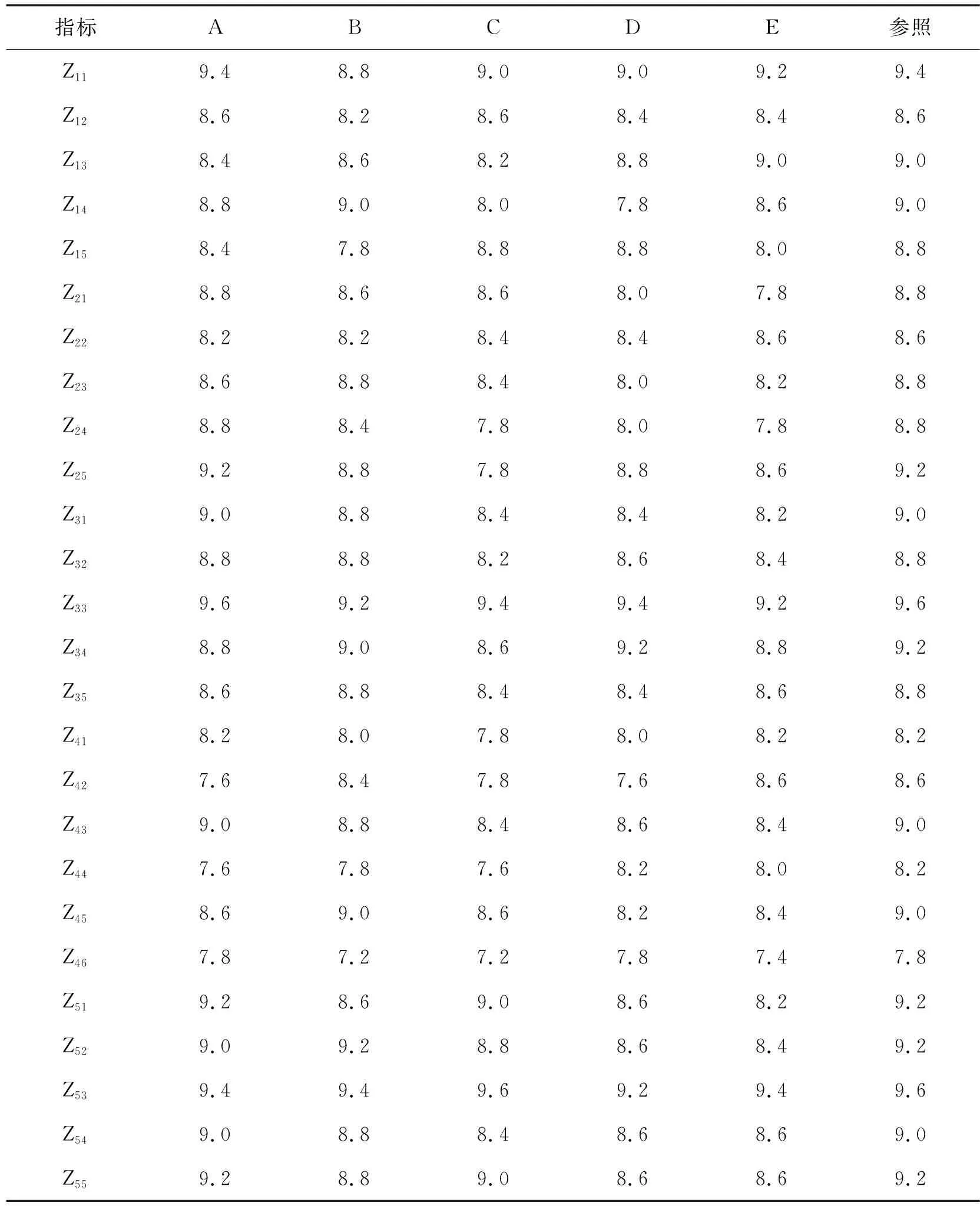
表2 底层指标专家组评判值

表3 各专业的专业评估底层指标灰色关联系数

见表1“专业设置Z1”的5个二级指标的权重向量为：

见表3及公式(2)，5个专业的“专业设置Z1”灰色关联评判矩阵为：

这里要注意，表3中的关联系数排列与评判矩阵之间有一转置关系。由公式(3)，“专业设置Z1”的评价结果向量为：

即5个专业的一级指标“专业设置Z1”评判结果与最优参照的关联系数分别为0.821、0.747、0.653、0.618、0.724。

对其他4个一级指标进行类似计算，结果为：

综上，由公式(2)，评价目标“专业评估Z”的灰色关联评判矩阵为：

见表1评价目标“专业评估Z”的权重向量为：

结合公式(3)，评价目标“专业评估Z”的评价结果向量为：

即5个专业的评价目标“专业评估Z”评判结果与最优参照的关联系数分别为0.857、0.781、0.634、0.615、0.635。如果以最优参照为满分10分，那么这5个专业的专业评估得分就是8.57、7.81、6.34、6.15、6.35。进一步观察评价目标“专业评估Z”的灰色关联系数矩阵可以发现，A专业“专业设置”“专业团队”“教学保障”“教学实施”“人才培养质量”等5个一级指标的得分分别为8.21、8.99、9.27、7.22、9.11；B专业5个一级指标得分为7.47、7.39、8.68、7.99、7.46；C专业5个一级指标得分为6.53、6.27、5.79、5.56、7.46；D专业5个一级指标得分为6.18、5.59、7.03、6.25、5.78；E专业5个一级指标得分为7.24、5.75、6.05、7.35、5.66。

3 结语

参与评估的5个专业中，A专业情况最好，但教学实施方面相对薄弱；B专业次之，在专业设置、专业团队、人才培养质量3个方面不够理想；C、D、E等3个专业评价结果较差，与A、B两个专业有较大差距。另外，C专业前4个一级指标的综合评价较差但“人才培养质量”尚可，说明该专业的专业建设存在退步现象，只是还没有完全反映到人才培养质量上来。上述评估结果得到各专业教师、二级院部领导等各方面的高度认可，说明本文所采用的指标体系全面、准确，所构建的灰色关联综合评价模型科学可行。