组合重力场模型的精度及其适用性分析
马艳鸽,郭春喜,张盼盼
(1.长安大学 地质工程与测绘学院,陕西 西安 710064;2.国家测绘地理信息局大地测量数据处理中心,陕西 西安 710054)
高分辨率、高精度的地球重力场模型在利用GNSS技术计算正常高中发挥重要的作用[1-2]。随着卫星重力计划的实施,重力场模型的精度和分辨率都得到很大改善,CHAMP、GRACE、GOCE等重力卫星使得全球重力场模型的中低阶的精度提高两个量级或者更高[3-4]。现阶段主要的超高阶重力场模型有EGM2008、GECO及EIGEN-6C4等,EGM2008利用地面重力数据、GRACE卫星重力数据、卫星测高数据等共同解算获得[5]。GECO重力场模型由GOCE低阶重力场模型TIM_R5联合EGM2008得到,前0~359阶利用GO_CONS_GCF_2_TIM_R5重力场模型的0~250阶结合EGM2008重力场模型的0~359阶计算得到,360~2 190阶与EGM2008的360~2 190阶保持一致[6]。EIGEN-6C4重力场模型利用地面重力数据、卫星重力数据(GOCE、GRACE、LAGEOS)、卫星测高数据等共同解算获得[7]。而EGM2008和EIGEN-6C4重力场模型在解算的过程中除利用卫星测量的数据之外,还有一些地形数据或者地面重力数据,存在一些长波段的误差,另外,GECO含有EGM2008模型的信息,同样存在长波段的误差,这些误差会传递到重力场模型求解的高程异常中,从而影响所得高程异常的精度[8]。为解决这一问题,可利用纯卫星重力场模型选择合适的截断阶次替换高阶重力场模型相对应的阶次,纯卫星重力模型完全由卫星数据独立解算,不依赖地面重力数据,因此不受地面数据长波段误差的污染。本文在分析EGM2008、GECO及EIGEN-6C4 3个超高阶重力场模型计算高程异常精度的基础之上选择GOCO03S、GO_CONS_GCF_2_DIR_R5、GO_CONS_GCF_2_SPW_R2以及GO_CONS_GCF_2_TIM_R5等4个纯卫星重力场模型实验分析,选取合适的截断阶次确定组合重力场模型并对其进行精度分析,最后探讨组合重力场模型在GNSS高程拟合中的应用。
1 原理与方法
1.1 模型的精度检核
利用GNSS/水准数据进行重力场模型的精度检核,计算P点的模型高程异常ξp,则GNSS/水准确定高程异常的方法为
ξGNSS/水准=H-h.
(1)
式中:H为GNSS实测的大地高;h为水准实测的正常高。可以得到残差高程异常为
Δξ=ξp-ξGNSS/水准.
(2)
利用式(3)进行重力场模型的精度评定。
(3)
1.2 组合重力场模型的确定
超高阶重力场模型EGM2008、GECO、EIGEN-6C4存在着由地面数据引起的长波误差,因此选择GOCO03S、GO_CONS_GCF_2_DIR_R5、GO_CONS_GCF_2_TIM_R5以GO_CONS_GCF_2_TIM_R5等4个纯卫星重力场模型进行实验分析,进一步选择合适的模型的截断阶数替换EGM2008、GECO、EIGEN-6C4重力场模型相应的阶数。主要步骤为:①选择合适的纯卫星重力场模型截断阶数N。②组合重力场模型的0~N阶由纯卫星重力场模型得到,N~2 190阶由超高阶重力场模型相应的阶补充得到。因此,组合重力场模型的确定关键是模型的截断阶数的确定,截断阶数的确定是利用GNSS/水准数据检核组合重力场模型的精度进行确定的,具体的步骤为:
1)对纯卫星重力场模型选择截断阶数k(k=10,20,30…N;N为纯重力场模型的最大阶数),组成新的重力场模型,新模型的0~K阶由纯重力场模型获取,K~2 190阶由超高阶重力场模型相应的阶补充得到。
2)利用新的重力场模型计算GNSS点对应的模型高程异常,由式(2)计算残差高程异常,然后由式(3)计算模型的精度。
3)选择精度最高的模型为最终的组合重力场模型,其对应的阶数k为最佳的截断阶数。
1.3 组合重力场模型在GNSS高程拟合中的应用
GNSS高程拟合的模型很多,本文以多面函数拟合模型进行GNSS高程拟合,GNSS高程多面函数拟合模型的基本原理是将残差高程异常用多个曲面高度逼近,建立数学模型,借此可以求解未知点的高程异常[9]。多面函数的数学表达式可以表示为
(4)
式中:Δξi为高程异常值;ai为待定系数;Q(x,y,xi,yi)为核函数,本文选择的核函数为双曲面核函数,具体形式为
(5)
其中δ为光滑系数。
2 算例分析
本文选取长江南京段控制网数据进行重力场模型精度及适用性分析,总共有53个高精度的GNSS控制点,每个点位都有基于WGS-84坐标系下的大地坐标以及二等水准高程数据。图1为点位分布图。
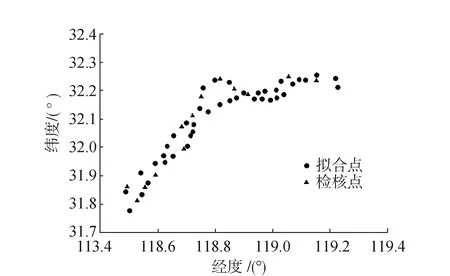
图1 点位分布图
2.1 超高阶重力场模型精度分析
对EGM2008、GECO及EIGEN-6C4超高阶重力场模型,分别计算53个GNSS控制点对应的模型高程异常,并与GNSS/水准实测的高程异常做比较,结果见表1。

表1 超高阶模型与GNSS/水准的高程异常比较结果 m
在本实验区域,从表1可以看出: 3个超高阶重力场模型的精度都达到了厘米级;EGM2008重力场模型的精度稍高于GOCE和EIGEN-6C4模型的精度。
2.2 组合重力场模型确定
组合重力场模型确定的关键是对纯卫星重力场模型截取可靠的阶次,对EGM2008、GECO及EIGEN-6C4超高阶重力场模型利用纯卫星重力场模型进行不同阶次的组合,得到各自对应的组合重力场模型(例如:GOCO03S/ EGM2008、GOCO03S/ GECO、GOCO03S/ EIGEN-6C4等,具体表示纯卫星重力场模型与超高阶重力场模型的组合重力场模型)。利用1.2中的原理分别对EGM2008、GECO及EIGEN-6C4超高阶重力场模型对应的组合重力场模型进行精度分析,精度结果分别见图2—图4。

图2 EGM2008对应的组合重力场模型精度趋势
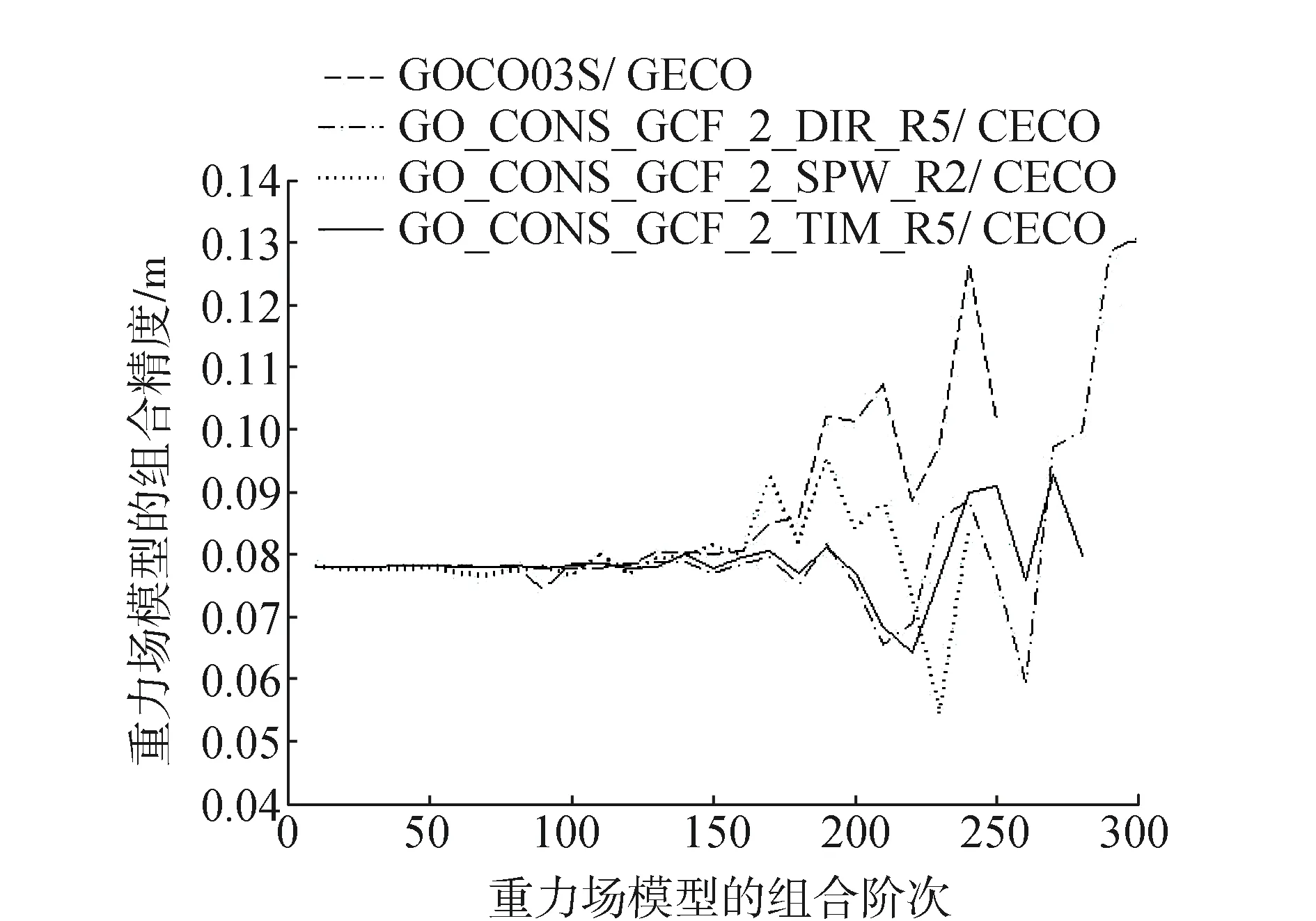
图3 GECO对应的组合重力场模型精度趋势

图4 EIGEN-6C4对应的组合重力场模型精度趋势
由图2—图4可以看出超高阶重力场模型EGM2008、GECO及EIGEN-6C4对应的组合重力场模型在150阶前的精度趋势基本一致,在150阶以后各组合重力场模型的精度趋势表现出明显的差异。可以选择精度最高时对应的阶次为组合模型的可靠截取阶次,由图2可以看出组合重力场模型GOCO03S/ EGM2008、GO_CONS_GCF_2_DIR_R5/EGM2008、GO_CONS_GCF_2_SPW_R2/EGM2008及GO_CONS_GCF_2_TIM_R5/EGM2008的可靠截取阶 阶次分别为90、260、230及220。由图3可以看出组合重力场模型GOCO03S/ GECO、GO_CONS_GCF_2_DIR_R5/GECO、GO_CONS_GCF_2_SPW_R2/GECO及GO_CONS_GCF_2_TIM_R5/GECO的可靠截取阶次分别为90、260、220及230。由图4可以看出组合重力场模型GOCO03S/ EIGEN-6C4、GO_CONS_GCF_2_DIR_R5/ EIGEN-6C4、GO_CONS_GCF_2_SPW_R2/ EIGEN-6C4及GO_CONS_GCF_2_TIM_R5/ EIGEN-6C4的可靠截取阶次分别为90、260、230及260。
2.3 组合重力场模型的精度分析
利用2.2中得到的组合重力场模型以及EGM2008、GECO及EIGEN-6C4超高阶重力场模型计算实测GNSS点位的高程异常值,并与GNSS/水准实测的高程的高程异常值比较,结果见表2—表4,由表2—表4得到的重力场模型精度结果见图5。

表2 EGM2008及其对应的组合重力场模型与实测高程异常比较结果 m
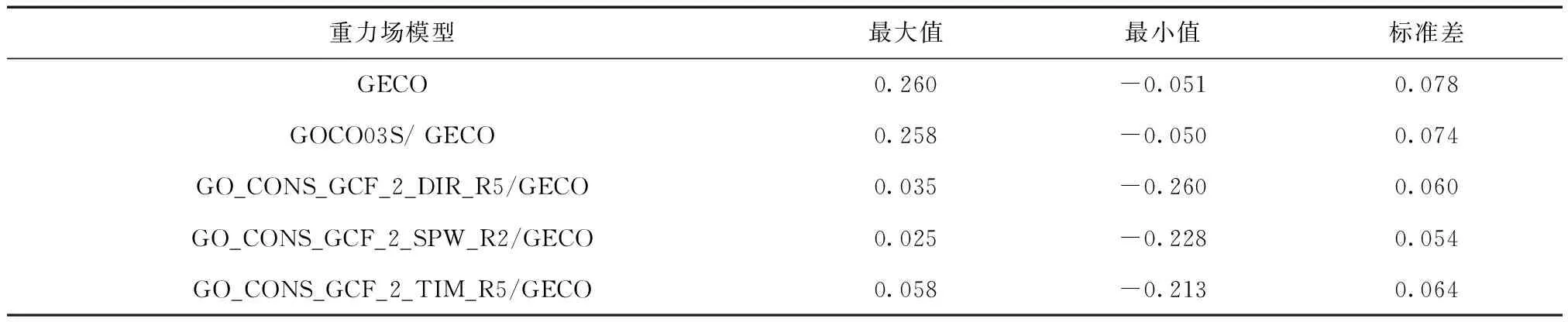
表3 GECO及其对应的组合重力场模型与实测高程异常比较结果 m

图5 重力场模型精度结果
由表2可以看出:在实验区域,EGM2008对应的组合重力场模型精度最优为0.061,最差为0.072,而EGM2008的精度为0.074,因此高程异常的精度最高提升18%;组合重力场模型的精度比EGM2008的精度都要高,见图5。
由表3可以看出:在实验区域,GECO对应的组合重力场模型精度最优为0.054,最差为0.074;而GECO的精度为0.078,因此高程异常的精度最高提升31%;组合重力场模型的精度比GECO的精度都要高,见图5。
由表4可以看出:在实验区域,EIGEN-6C4对应的组合重力场模型精度最优为0.059,最差为0.077;而EIGEN-6C4的精度为0.078。因此高程异常的精度最高提升24%;组合重力场模型的精度比EIGEN-6C4的精度都要高,见图5。
综合表2、表3、表4及图5可以看出:4种纯卫星重力场模型截取可靠阶次后对EGM2008、GECO及EIGEN-6C4模型精度提升能力从大到小以此为GO_CONS_GCF_2_SPW_R2、
GO_CONS_GCF_2_DIR_R5、GO_CONS_GCF_2_TIM_R5、GOCO03S。GO_CONS_GCF_2_SPW_R2
对于精度提高影响最明显,GOCO03S对于精度提高影响最小。
2.4 组合重力场模型在GNSS高程拟合中的应用
根据图1的选点方案,其中40个点为拟合点,13个点为检核点。利用2.3中得到的精度最高的组合模型(GO_CONS_GCF_2_ SPW_R2/EGM2008、GO_CONS_GCF_2_SPW_R2/GECO、GO_CONS_GCF_2_SPW_R2/ EIGEN-6C4)以及高阶重力场模型(EGM2008、GECO、EIGEN-6C4),基于1.3中的原理,采用多面函数拟合法进行GNSS高程拟合,检核点与GNSS/水准比较结果见表5。

表5 检核点与GNSS/水准比较结果 m
从表5可以看出,利用EGM2008、GECO及EIGEN-6C4超高阶重力场模型进行高程拟合的精度与利用组合重力场模型进行高程拟合的精度相当,这说明EGM2008、GECO及EIGEN-6C4超高阶重力场模型存在的长波段误差也可通过一定的拟合模型进行削弱。
3 结束语
本文进行了组合重力场模型的精度及其适用性分析,得出以下结论:
1)在本实验区域,GNSS/水准数据检核表明, EGM2008、GECO及EIGEN-6C4超高阶重力场模型的精度都达到厘米级,且EGM2008重力场模型的精度稍高于GOCE和EIGEN-6C4模型的精度。
2)利用GNSS/水准数据检核组合重力场模型表明,组合重力场模型能提高重力场模型精度。EGM2008对应的组合重力场模型精度比EGM2008精度至少提高3%,最优提高18%。GECO对应的组合重力场模型精度比GECO精度至少提高5%,最优提高31%。EIGEN-6C4对应的组合重力场模型精度比EIGEN-6C4精度至少提高2%,最优提高24%。
3)4种纯卫星重力场模型截取可靠阶次后对EGM2008、GECO及EIGEN-6C4精度提升能力影响最大的是GO_CONS_GCF_2_SPW_R2,影响最小的是GOCO03S。
4)利用EGM2008、GECO及EIGEN-6C4超高阶重力场模型进行高程拟合的精度与利用组合重力场模型进行高程拟合的精度相当,这说明EGM2008、GECO及EIGEN-6C4超高阶重力场模型存在的长波段误差也可通过一定的拟合模型进行削弱。

