厦门CORS基准站稳定性分析

谢继香，雷海智，张洪银

(1.青海省水文地质及地热地质重点实验室，青海 西宁 810008;2.青海省水文地质工程地质环境地质调查院，青海 西宁 810008)

厦门市位于北东向长乐—诏安深大断裂带与东西向南靖—厦门断裂带交接部位。区域构造位置属于“闽东燕山断坳带”、“闽东南沿海变质带”的组成部分[1]。利用厦门境内的CORS基准站长时间监测地表位移，能够有助于探索区域地壳运动情况。

CORS系统可定义为将基准站网通过网络互联，构成以提供位置和时间信息为核心的网络化综合服务系统。本文采用GAMIT/GLOBK[2-3]软件计算厦门CORS基准站2013-2015年间GPS观测数据，分析时间序列的噪声模型和周期特性，获得较为干净的GPS速度场,这对更好地评价厦门区域CORS基准站的稳定性，保障厦门市现代大地坐标框架的时效性有重要意义。

1 数据处理

采用麻省理工学院(MIT)、斯克里普斯海洋研究所(SIO)研制的GAMIT/GLOBK 10.5软件对基线进行解算，选取中国境内及周边的21个IGS站(aira、artu、bako、bjfs、daej guam、hyde、iisc、irkt、kit3、lhaz、nril、ntus、pimo、pol2、shao、tnml、ulab、urum、 wuhn、yakt)作为约束(水平方向0.025 m，垂直方向0.050 m)于ITRF08框架[4-5]。

GAMIT基线解算策略见表1，加入月球历表(luntab.)、太阳历表(soltab.)、章动表(nuttab.)、地球自转表(UT1.)、海洋潮汐(grid.oct)、对流层延迟(vmf1.grd)、闰秒(leap.sec)、天线相位中心改正。以此，最大程度地修正日、月潮引力极潮(pole tide)、固体潮(solid tide)及海潮(ocean tide)对观测GPS站点造成的影响。另外，解算过程中进行卫星轨道模型、大气压模型、水汽分布模型、多路径效应、天线相位中心等改正。

表1 GAMIT解算模型和参数设置

利用GAMIT/GLOBK软件计算厦门区域内的6个GPS连续观测站2013—2015年数据，获得多年的连续时间序列资料，解算策略如表1所示。对于GPS时间序列资料的分析，通常需要考虑长期的周期运动、同震变形以及震后变形。GPS单站、单分量坐标序列用非线性模型表示[6]为

y(ti)=a+bti+csin(2πti)+

dcos(2πti)+esin(4πti)+fcos(4πti)+

(1)

式中：ti是以年为单位；系数a，b分别代表地壳位置和线性变换率；系数c，d，e，f描述周年和半周年运动振幅；系数gj代表地震造成的同震位移；系数hj表示震后地壳运动速度的改变量；系数kj描述震后变形呈指数衰减的现象；H(t)为阶跃函数(Heaviside step function)；τj为松弛时间；vi为残差。

当vi与时间无关(高斯白噪声)，也就是期望E(vi)=0时，式(1)可以利用最小二乘求解各个参数，获得测站速度及其中误差。然而，大量研究发现，GPS时间序列残差并非随机过程，不能通过大量观测资料消减误差影响。

2 噪声分析

GPS时间序列存在噪声来源，如季节性的降雨造成土壤膨胀收缩，进而使测站点位不稳定；另外GPS资料求解时引入了不正确或者不完善的卫星轨道模型、大气模型或天线相位中心的校正不准确等。

对GPS时间序列进行噪声分析主要有两个目的：①为估计合理的GPS误差，若GPS时间序列内含有与时间相关的噪声，则以高斯分布为基础的最小二乘所估计的速度场误差将会被低估；②为了解不同类型的布点方式对GPS长期观测造成的影响。

原始时间序列扣除拟合值后的噪声时间序列，可以用频谱定性分析噪声的类型。频谱分析是一种在频率域上分析信号的方法。噪声时间序列在频谱域上的功率谱可以使用power law的形式表示[7-10]为

(2)

式中：f是频率；P0和f0是常数；k是谱指数，通常为介于-3到1之间的任意实数，其中整数k代表一些特殊的噪声类型：k=0时是标准的白噪声(white noise，WN)、k=-1时是标准的闪烁噪声(flicker noise，FN)、而k=-2时则是标准的随机漫步噪声(random walk noise，RWN)。另外，除了标准的白噪声以外，其余的部分统称为有色噪声。

计算发现6个站点的三分量噪声的谱指数k介于-0.6～0之间，可以判断“白噪声+闪烁噪声”(“WN+FN”)是最佳噪声模型。图1中可以看出，频率为1和2时，存在明显突起，这说明数据中存在周期为1年和半年的周期波动。确定了最佳噪声模型以后，本文采用CATS(Create and Analyse Time Series)软件对厦门CORS连续站数据进行噪声分析。

CATS软件是由Williams[5]开发的一个独立的C程序，是比较连续GPS坐标时间序列中的随机噪声过程的软件，是以命令行计算参数，数据输入以文件形式，具体的格式与说明参考安装目录下的用户手册。

使用--sinusoid来控制求取年周期和半年周期。使用-sinusoid 1y求解年正弦曲线；使用-sinusoid 1y1求解年和半年正弦曲线。其他更详细的控制参数可以参见CATS的使用者操作手册。

为了比较噪声模型对分析结果的影响，CATS软件分别对同一批资料进行WN模型分析和“WN+FN”模型分析， GPS连续观测数据在时间序列分析的过程中，最常被考虑到的通常是地震相关的修正模型参数与长周期的变动。例如同震造成的时间序列不连续，震后的异常活动，更或是季节性的变化等等[11]。但最基本的就是测站的线性变化，也就是速度项。因此以速度项的模型结果，作为探讨比较的重点。

例如：

cats --model pl:k-1 --model wh: --columns 7 --sinusoid 1y1 --verbose --output fn_wn.KKN4 KKN4_CATS.neu

cats --model wh: --columns 7 --sinusoid 1y1 --verbose --output wn.KKN4 KKN4_CATS.neu

图1 XMJM的功率谱图，谱指数介于-1～0之间

表2列出时间序列分析后部分测站之东西、南北、与垂直三分量的速度值，其中每一测站横栏中上方为经过噪声模型“全频等幅杂波+闪变杂波”( “WN+FN”)处理分析的结果，下方则没有经过噪声模型分析(WN)。结果指出，没有使用噪声处理，模型参数的误差将明显被低估[6]。其中位于误差后面的常数是两者误差的倍数，平均而言，经过噪声处理后的模型误差在东西、南北和垂直方向约为原本的6.7、5.9和6.0倍。换言之，若未有考虑时间序列中时间相关的噪声，误差将被低估约6倍左右。厦门境内连续GPS站点分布在ITRF08框架下2013—2015年间速度场绘制于图2，左边是水平速度场，右边是垂直速度场。

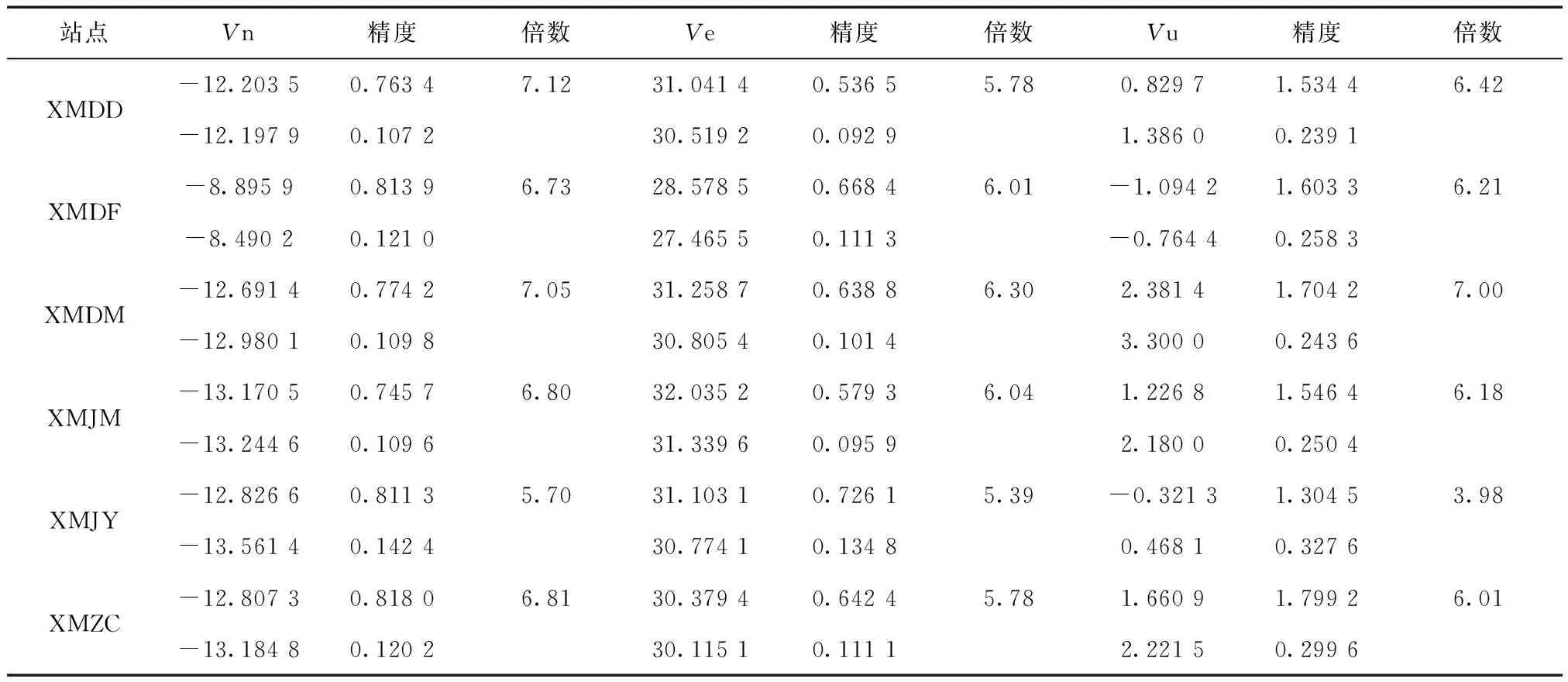
表2 时间序列分析结果，测站的东西、南北、垂直三分量的速度值及误差 mm

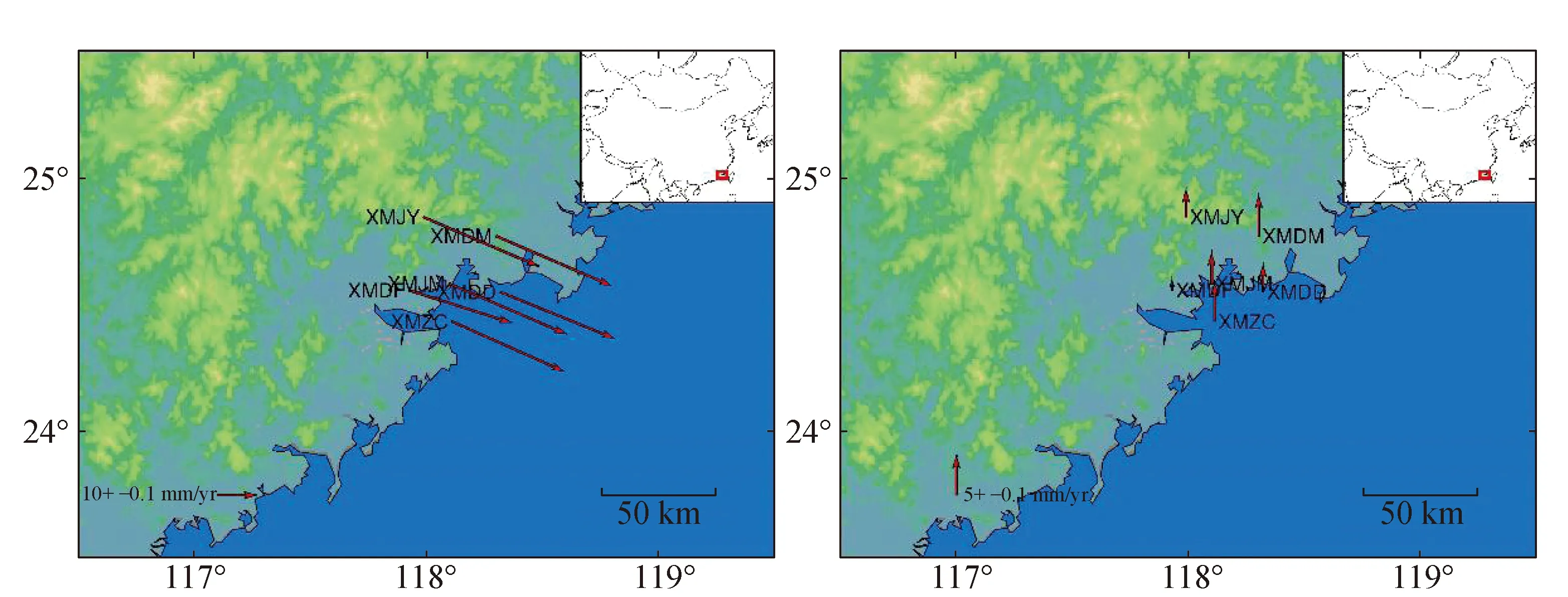
图2 厦门境内连续GPS站点分布和ITRF08框架下2013-015年间速度场

3 结束语

本文利用GAMIT/GLOBK软件对2013—2015年厦门地区3年连续观测的GPS数据进行解算并对时间序列进行噪声分析。结果表明，厦门境内连续站的最佳噪声模型是“WN+FN”，若未考虑时间序列中时间相关的噪声，速度场估算误差将被低估6～7倍。本文最后获得厦门地区的精确GPS速度场模型，研究结果有助于了解厦门区域构造及地壳形变，并对区域坐标框架维护有重要作用。