粒子群算法及多阈值指数熵的遥感影像变化检测方法研究
黄 亮, 王铭佳,吴俐民
(1.昆明理工大学 国土资源工程学院,云南 昆明 650093;2.昆明市测绘管理中心,云南 昆明 650050)
多时相遥感影像变化检测是利用同一区域但不同时期的遥感影像,定量地分析和识别出地表覆盖变化的特征、过程和区域。其中,对于对地表宏观变化进行动态监测,仍主要采用LANDSAT 4~8和MODIS为代表的中、低空间分辨率遥感影像作为主要数据源。目前,采用中、低空间分辨率遥感影像进行地表宏观变化动态监测已应用于诸多领域,如城市扩张[1]、土地利用现状/土地覆盖变化[2-3],河流及湖泊时空演变[4]、土地石漠化演变[5]等。
几十年来,诸多国内外研究人员针对中、低空间分辨率遥感影像变化检测技术开展了大量研究,并提出很多有效的方法。这些方法主要包括两种思路:分类后比较和直接比较法[6]。其中,直接比较法是对两幅具有相同地理区域但不同时期的遥感影像进行逐像素比较得到可靠的变化检测图的方法[7],由于该方法具有便于理解,易于实现的优点,因而被广泛用于中、低空间分辨率遥感影像变化检测。直接比较法涉及的关键技术有差异影像构造和变化阈值选取。目前,变化阈值选取方法有很多[8],如:Ridler and Calvard algorithm[9]、Tsai (1984) algorithm[10]、Otsu algorithm[11]、Rosin algorithm[12]、Maximum Shannon Entropy Method[13]等。这些方法中,基于熵概念的方法是一种颇受研究者关注的阈值选取方法[14],但以Shannon熵为代表的信息熵存在信息易丢失的问题。为了解决该问题,Pan and Wu提出了一种双阈值指数熵的阈值选取办法,并取得了较为理想的分割效果,减少了信息的损失[15]。对于细节复杂,目标地物较多的图像,采用多阈值分割可更有效地分割出背景和多个目标[16]。综合考虑遥感源和运算量,本文选取三阈值指数熵来对构造的差异影像进行分割获取变化区域。
针对多时相遥感影像变化检测的需要,本文提出基于多阈值指数熵的遥感影像变化检测方法。同时,针对指数熵方法因阈值数量增加,而带来的阈值选取难和运算量增大的问题,本文引入粒子群算法,提出一种基于粒子群算法及多阈值指数熵的遥感影像变化检测新方法。采用粒子群优化算法寻找三阈值指数熵的最优阈值,并将得到的阈值用于差异影像分割,从而识别差异影像中变化区域和非变化区域。实验结果表明,该方法能准确分割差异影像得到变化区域,是一种有效、可行的变化检测方法。
1 基本原理
1.1 三阈值指数熵法基本原理
假定原始差异影像大小为M×N,灰度级取0,1,…,L-1,假定阈值t将影像分为目标(变化类)和背景(非变化类)两大类,Pi为灰度级i的像素出现的概率,则目标部分的熵为[15]
(1)
背景部分熵为
(2)
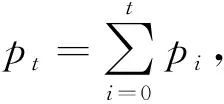
最佳阈值t*满足:
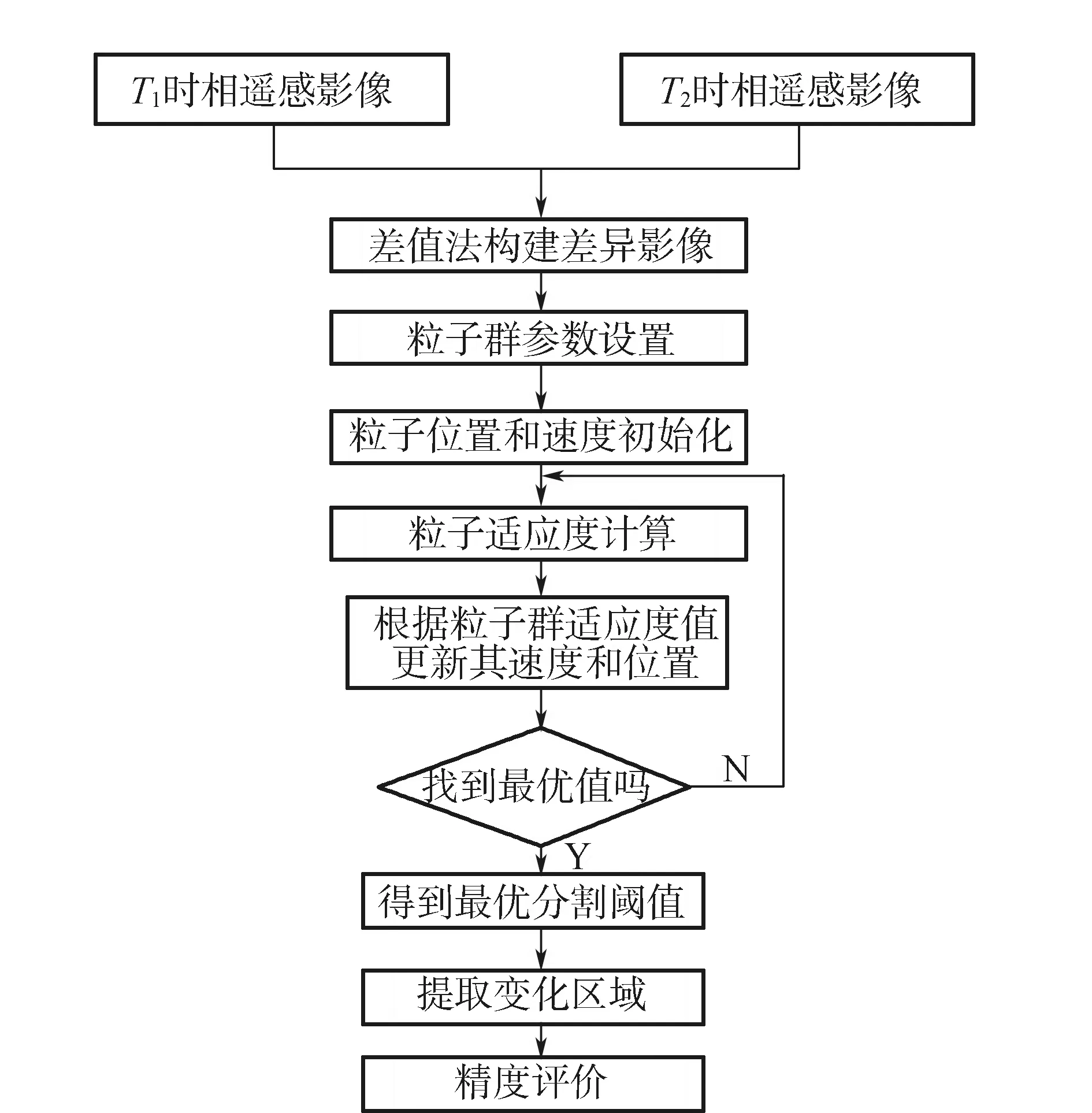
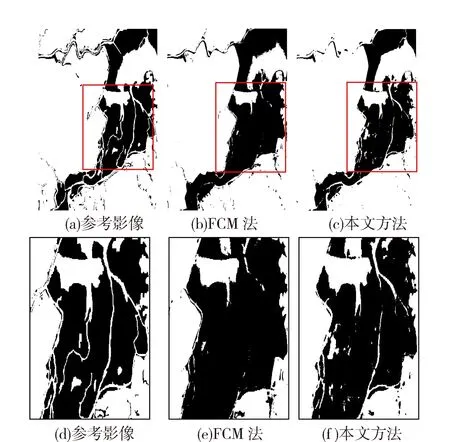
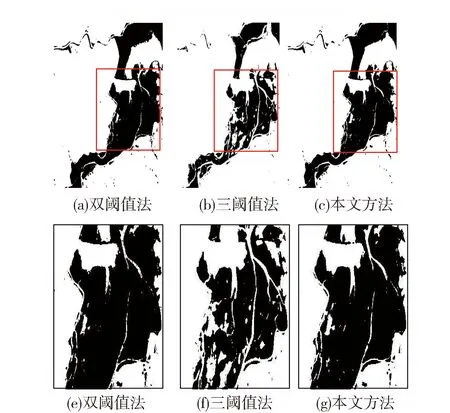
T(t*)=Argmax0 Hunchange(t)}. (3) 将指数熵法扩展到三阈值分割时,则有3个阈值t1,t2和t3;将图像分为4类C0,C1,C2和C3,其中: C0={0,2,…,t1}, C1={t1+1,t1+2,…,t2}, C2={t2+1,t2+2,…,t3}, C3={t3+1,t3+2,…,L-1}。 (4) (5) (6) (7) 其中: H(C1)+H(C2)+H(C3)}. (8) PSO[17]是一种有效的全局寻优算法,是由Kennedy和Eberhart于1995年提出的。该算法起源于一种简单的社会模拟现象,最初设想是模拟对鸟群觅食的过程,后来学者们渐渐将PSO作为一种优化工具进行广泛的应用。PSO优化算法和其他的优化算法类似,即将寻优的参数组合成群体,通过对环境的适应度来将群体中的个体向好的区域移动。与其他算法的不同之处在于,PSO优化算法在描述个体时,将其看作D维空间中一个没有提及的微粒(点),在每一次迭代中,通过将微粒的历史最佳位置——个体极值pbest和群体的历史最佳位置——全局极值gbest结合起来, 来更新每个粒子的速度和位置。 (9) (10) 式中:k为迭代次数;xi,vi分别为第i个随机粒子的位置和速度;c1,c2为学习因子,通常c1=c2=2;r1,r2为介于(0,1)之间的随机数;w为权重。 PSO算法概念简单、容易实现,搜索速度快范围大,与其它优化算法相比,它的优点较为突出。 假定f和g分别为T1和T2时期获取的同一地理区域经几何配准的两幅遥感影像,影像大小均为M×N像素。由于由配准误差引起的虚检像素基本分布在边缘附近1个像素的范围内,为了保证变化检测精度,本文在前期对两幅遥感影像进行精确配准,将配准误差控制在0.6个像素。f={f(x,y),1≤x≤M,1≤y≤N}和g={g(x,y),1≤x≤M,1≤y≤N},f(x,y)和g(x,y)分别表示影像中第x行、第y列的灰度值。为了实现利用粒子群算法及三阈值指数熵的遥感影像非监督变化检测方法,其流程图如图1所示。 1)差异影像构造。采用灰度差值法构造差异影像。图像差值法是指对T1和T2时相的遥感影像中对应的像素值进行减法运算。采用的差值法为 D(x,y)=255-|f(x,y)-g(x,y)|, (11) 0≤f(x,y)≤255,0≤g(x,y)≤255. (12) 式中:f(x,y)和g(x,y)分别为不同时相影像上第x行、第y列像素的灰度值;D(x,y)为用灰度差值法构造的差异影像。若一个像素未发生改变,则D(x,y)=255,反之,如果这个像素的变化程度越大,那么D(x,y)就离0越近。 3)变化检测精度评价。为了定量定性的评价提出方法的有效性,本文通过总体错误率、虚检率和漏检率3个指标来定量评价变化检测的精度[18]。 图1 提出方法流程 为了验证提出方法的可行性和准确性,选取一组多时相遥感影像作为实验数据。实验区为鄱阳湖某局部区域,获取时间分别为1989年7月(如图2(a))所示和2010年1月(如图2(b))所示。两期影像均为空间分辨率为30 m的Landsat-5遥感影像。影像数据来源于中国科学院数据云网站中的地理空间数据云。两期遥感影像的大小均为510像素×510像素,变化区域参考图如图3(a)所示,黑色区域为变化区域。其中,变化的像素为69 413像素,未变化的为190 687像素,参考影像主要是通过人工解译而得到。 实验设计了2组对比实验,第1组是本文方法与利用FCM算法[19]的非监督变化检测方法[20]进行对比;第2组是本文方法与利用双阈值指数熵、三阈值指数熵的非监督变化检测方法进行对比。 图3(b)为利用FCM算法的非监督变化检测方法得到的结果图,图3(c)是采用本文方法得到的结果图。图3(d)、3(e)和3(f)分别对应于图3(a)、3(b)和3(c)中的矩形框区域。实验分别对以上两种方法进行精度评价,结果如表1所示。从表1可见,采用本文方法,虚检的变化像素为6 712像素,虚检率为3.52%;总体错检像素13 612像素,总体错检率为5.23%。从纵向来比较,本文方法相较于FCM法来说,虚检的像素数少了7 692个,总体错检像素少了5 628个,总体错检率低了2.17%。对比图3中的3幅变化图可以看出,FCM法将较多未变化支流错检为变化区域,导致了错检率的上升;而本文方法对部分支流给出了正确的识别。在虚检率、漏检率以及总体错检率3项指标中,本文方法在虚检率和总体错检精度2项指标中优于FCM法。实验表明,本文方法是一种有效地、可行的变化检测方法。 图4(a)是采用双阈值指数熵的非监督变化检测方法得到的结果图,图4(b)是采用三阈值指数熵的非监督变化检测方法得到的结果图,图4(c)是采用本文方法得到的结果图。图4(d)、4(e)和4(f)分别对应于图4(a)、4(b)和4(c)中的矩形框区域。实验分别对以上3种方法进行精度评价,结果如表2所示。从表2可见,本文方法相较于双阈值指数熵法,总体错检率有小幅降低。虽然本文方法和传统三阈值指数熵法都是采用三阈值指数熵对差异影像进行分割,但由于阈值选取方法的差异,选取的阈值也不同,变化检测结果存在较大差异。提出方法存在较低的虚检率,而传统三阈值指数熵法则是存在较低的漏检率。本文方法相较于传统三阈值指数熵法,总体错检率降低了2.21%。对比图4中的三幅变化图可以看出,本文方法得到的变化结果图略优于双阈值指数熵法,明显优于三阈值指数熵法的变化结果图。 在运算时间方面,由于提出方法采用了PSO优化算法,有效地提高了算法的运算速度,保证了算法的高效性。采用提出方法的运行时间为1.980 5 s,而采用传统三阈值指数熵法则用了29.028 4 s。实验结果表明,采用提出方法可大幅提高运算速度。 图3 第1组对比实验变化检测 图4 第2组对比实验变化检测 变化检测方法虚检率/%漏检率/%总体错检率/%FCM法 14 404像素7.554 836像素6.9719 240像素7.40本文方法6 712像素3.526 900像素9.9413 612像素5.23 表2 第2组实验虚检率、漏检率以及总体错检率 对于细节复杂、目标地物较多的影像,采用多阈值可提高阈值分割的精度,但阈值数量的增加势必会增加计算难度和运算量,从而造成大量时间的耗费。针对该问题,采用PSO算法选取三阈值指数熵法的最优阈值,并将其用于对构造的差异影像进行分割获取多时相遥感影像变化区域。本文以1989年和2010年获取的鄱阳湖某局部区域空间分辨率为30 m的Landsat-5遥感影像作为实验数据源。经实验验证,粒子群算法能快速、有效地搜索到全局最优的三个变化阈值,且得到的变化检测结果具有较高精度,正确率高达94.77%,优于FCM法、双阈值指数法及传统三阈值指数法。同时在运行时间上,提出方法相较于传统三阈值指数法有大幅提高。 本文提出的方法主要适用于中、低空间分辨率遥感影像,可用于流域时空变化分析、农村聚落分析、城市扩张分析、土地利用现状/土地覆盖变化、土地石漠化演变等。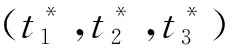
1.2 PSO基本原理
2 研究方法
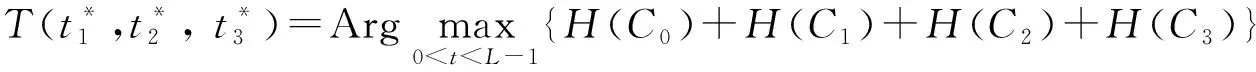
3 实验结果与分析
3.1 实验数据
3.2 实验结果分析


4 结 论

