基于三次样条函数的长线路GNSS高程拟合研究

张海燕，李秀海,韩 冰

(1.广东省佛山市南海区房地产测绘中心,广东 佛山 528220 ;2.黑龙江工程学院 测绘工程学院，黑龙江 哈尔滨 150050;3.哈尔滨测量高等专科学校测量工程公司，黑龙江 哈尔滨 150050；4.黑龙江测绘地理信息局 地理信息工程院，黑龙江 哈尔滨 150081)

GNSS高程拟合仍是目前测绘工程技术研究的热点，并取得了可喜的研究成果[1-9]。公路测绘GNSS高程拟合不断有测绘科技工作者进行理论研究和实践探索[10-12]。公路测绘具有测区狭窄和线状的特点，且高程控制测量等级以四等和等外水准测量为主。在面状、线状测区具有较多高等级高程控制点的情况下，已有的GNSS高程拟合研究成果已证明能够达到四等或更好的精度。由于国家已有高等级测量控制点破坏较严重，外业公路控制测量能够利用的高级水准点并不多，在高程起算点数量较少和拟合线路较长的情况下研究GNSS高程拟合的精度和可靠性更具有实际应用价值。已有公路GNSS高程拟合研究成果多以分区、分段，以线性、曲线模型拟合，需要较多的高程起算数据，实际工程很难满足。三次样条函数具有连续光滑的特点，对一些连续光滑的曲线物理模型具有很好的拟合效果，而线状区域大地水准面具有连续光滑的特性，因此利用三次样条函数对线状GNSS高程拟合具有很好的适应性。本文利用某道路改扩建工程的一级GNSS和四等高程控制网的工程实例，基于三次样条函数对GNSS高程拟合进行了研究，得到了一些有益的结论。

1 公路GNSS高程拟合常用的数学模型

公路GNSS高程拟合常采用以下线性模型、二次曲线模型和三次曲线模型：

ξ=a0+a1x,

(1)

ξ=a0+a1x+a2x2,

(2)

ξ=a0+a1x+a2x2+a3x2,

(3)

ξ=H大-h正.

(4)

式中:ξ为高程异常;x为拟合坐标(或是设计公路的里程数)。通过公共点的大地高和正常高，根据最小二乘原理可求出式(1)—式(3)中的系数ai，进而可求出拟合点的高程异常及正常高。

2 三次样条函数及三弯矩方程

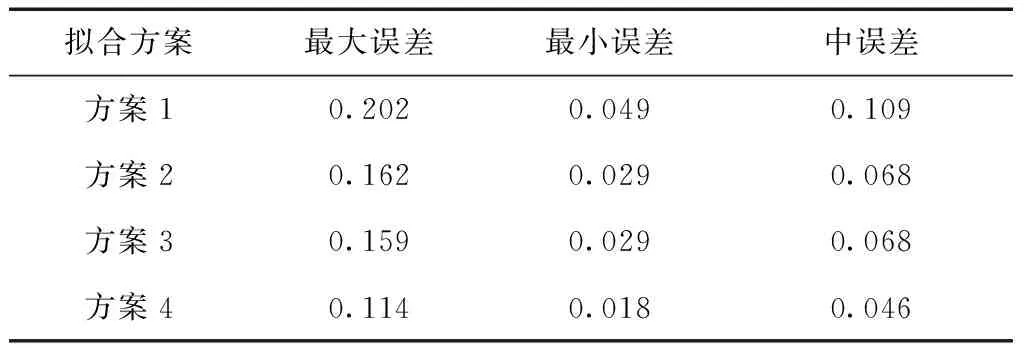
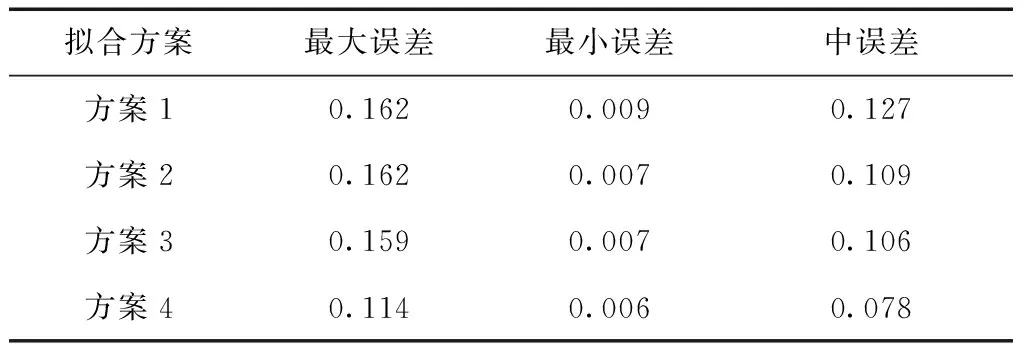
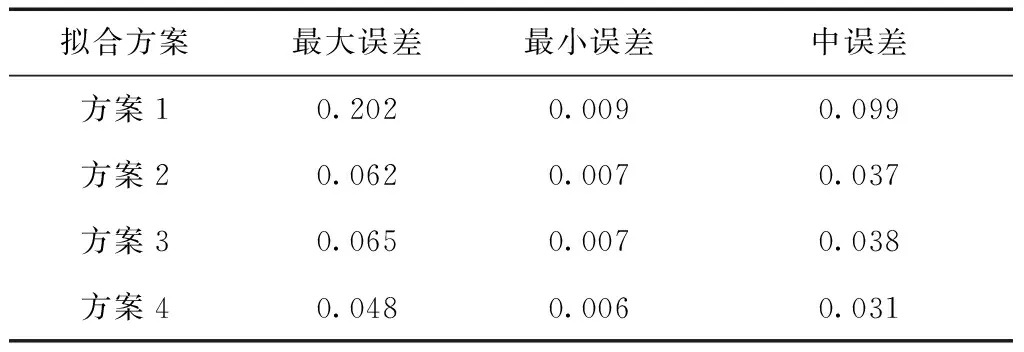
设有一剖分Ω，p1=x1

B(x)∈C2[p1，p2](即B(x)在闭区间[p1，p2]具有连续的一阶、二阶导数)。

B(x)在每一个子区间[xi,xi+1]上(j=1,2,…，n-1)是次数≤3的多项式，则称B(x)为关于剖分Ω的一个三次样条函数[13]。

设有函数f(x),其函数值表(xi，f(xi))，(i=1,2，…，n),如果三次样条函数B(x)满足插值条件

B(xi)=f(xi),(i=1,2,…,n).

称B(x)为f(x)的关于剖分Ω的三次样条插值函数。分段三次多项式函数可由Hermite插值函数表示，即B(x)在[xi,xi+1]的表达式为

B(x)=Bi(x)=yi+ai,1(x-xi)+

ai,2(x-xi)2+ai,3(x-xi)3.

(5)

(6)

其中Di是三次样条函数B(x)在节点处的二阶导数，即

B″(xi)=Di,(i=1,2,…,n).

确定三次样条函数需要求解Di，在满足自然边界条件D1=Dn=0的条件下，其它Di由下式求解

(7)

其中，

(8)

方程中的未知量Di在力学上解释为细梁在xi截面处的弯矩，且弯矩与其相邻两个弯矩有关，故方程(7)称为三弯矩方程。由方程(7)求出Di后，带入式(6)，即可确定三次样条差值函数。

3 实例分析

某高等级公路改扩建工程需要建立一级GNSS工程控制网和四等水准高程控制网。按规范要求，每5 km左右布设1对控制点，设计公路线路长度约83 km，全网共布设31个一级GNSS点，联测三等以上水准点5个，每个新布设的一级GNSS点均联测四等水准。线路约东西走向，故高程拟合以横坐标作为自变量。5个高级水准点分割的4段拟合路线长度由西向东分别为25 km、15 km、20 km、23 km。西部第1段经过矿区和山区，地貌起伏较大，最大高差约100 m，其余3段地势较平坦。GNSS控制网外业采用徕卡1 200双频GNSS接收机观测，采用边连接方式，每时段观测45 min以上，内业使用LGO软件解算，获得合格的三维无约束平差结果，并进行高程拟合计算。

设计如下4种高程拟合方案：

方案1：利用线性函数式(1)作为高程拟合模型；

方案2：利用二次曲线式(2)作为高程拟合模型；

方案3：利用三次曲线式(3)作为高程拟合模型；

方案4：利用基于三弯矩方程的三次样条函数进行高程拟合。

各种拟合方案及精度统计见表1和图1，拟合精度统计由式(9)计算。

(9)

其中，H正为正常高；H拟为拟合高程；n为拟合点的个数。

表1 全线路GNSS高程拟合误差精度统计 m

注：共31个点

图1 高程拟合误差曲线

由表1可看出，方案1利用线性模型进行高程拟合精度最低，而方案2和方案3分别采用二次曲线模型和三次曲线模型进行高程拟合精度基本相当，比方案1拟合精度有明显提高。方案4利用三次样条函数进行高程拟合中误差为4.6 cm，明显优于其它几种方法，表明用三次样条函数进行高程拟合是成功的。由图1可看出，方案4高程拟合误差曲线较平滑，震荡较小，显示该方法的优越性。在四种方案中，方案1高程中误差达dm级，表明对较长线路的GNSS高程拟合用单一的线性模型拟合是不合适的。其它几种方案拟合精度均高于方案1，达到cm级，拟合精度能够满足一般的测图需要，在实际公路勘察测量中可以选用。方案4在拟合线路较长、高程起算点较少的情况下，总体拟合精度小于5 cm，且拟合误差曲线较平滑，更接近于大地水准面的实际情况，具有较好的拟合效果。认真分析各方案，发现在线路的第1段(见图2，最西边2个高程起算点之间的设计路线)拟合误差最大，其余3段拟合效果均较好，分段统计精度如表2、表3所示。

图2 第1段公路线路

表2 第1段线路GNSS高程拟合误差精度统计 m

注：共10个点

表3 其余3段线路GNSS高程拟合误差精度统计m

注：共21个点

由表2、表3可看出，除方案1外，其它3种拟合方案第1段拟合的误差均较大，而其余3段拟合的中误差均小于4 cm。究其原因，主要有三：一是第1段线路两端高程起算点之间的线路长近25 km，线路较长；二是该段线路高差起伏较大，路线经过山区和矿区，大地水准面变化较大，期间仅有2个高程起算点很难准确拟合；三是该段线路非直线，呈U字形，而拟合坐标是以横坐标为自变量，与假定线路基本直线实际差别较大，但利用三次样条函数插值拟合精度仍达到cm级。

4 结束语

利用三次样条插值函数进行线路高程拟合，在拟合线路较长及高程起算点较少的情况下，仍能达到cm级的拟合精度。在地势较平坦地区，利用二次曲线和三次曲线进行线路高程拟合，拟合精度没有太大差别。在地形和线路变化较大地区，各种模型拟合误差均较大，如何提高此类线路的GNSS高程拟合精度需进一步研究。