基于PCA和SVM的管道腐蚀超声内检测*

唐东林,魏子兵,潘 峰,唐圳雄,李茂扬,胡 琳(西南石油大学机电工程学院石油天然气装备教育部重点实验室,成都 610500)

埋在地下的输油管线在运行一段时间后,受外部土壤及内部油水介质因素影响,管壁会遭受不同程度腐蚀,必须对管道腐蚀缺陷进行检测评判,以保证管道的安全运行[1]。超声波缺陷检测技术具有数据量小、检测精度高,速度快,缺陷定位准确的等优点而被广泛应用于管道缺陷检测与评判[2]。超声波缺陷信号识别对应着一种模式识别问题,常用的模式识别方法有神经网络和支持向量机。目前,国内外的学者对各类识别方法在超声波检测的缺陷信号识别上的应用做了大量的研究,戴波等[3]采用支持向量机和表征超声回波形态的A扫描数据作为特征向量有效地分类识别了管道腐蚀产生的突界面和腐蚀裂纹;周西峰等[4]基于BP神经网络和采用小波包分解后的各频谱能量特征作为特征向量,对缺陷类型识别问题进行了研究;Sambath S等[5]提出了一种提高超声探伤敏感性和缺陷分类的方法,应用神经网络和利用小波变换推导出包含各种缺陷的二维信息作为特征向量,研究表明,方法具有较高的可靠性和准确性;Jing Liu[6]等采用基于小波包变换和BP神经网络的方法,提取焊缝超声波回波信号的14种特征参数,对4种焊缝进行识别,实验结果表明,该方法具有很好的可行性。万振凯等[7]利用小波变换分解超声波A扫描信号,并将分解的各信号的能量作为特征,对三维编织复合材料微裂纹和孔隙进行分类识别,实验结果表明该方法对分析三维编织复合材料内部缺陷具有可行性。目前,在超声波缺陷信号识别研究中,用于识别分类的特征向量,存在许多冗余的特征,且每一个特征之间存在相关性,降低了腐蚀缺陷信号识别的正确率,因此有必要去除这些冗余的特征和消除特征之间的相关性。

主成分分析是一种通过降维的方法把高维的特征向量转化成少数几个主成分的方法,这些主成分能够反映原始特征向量的绝大部分信息,以及降低每一个特征之间的相关性。Garcia-Alvarez D[8]等利用主成分分析对过程状态进行监控,对故障进行诊断以及隔离等几种工作模式和长时间的瞬态和启动过程;Qingbo He等[9]通过内燃机声音分析和汽车变速箱振动分析的实验,利用主成分分析(PCA)技术从测量信号的时域和频域统计特征中自动提取主成分表示,对机器状态进行了有效可靠地监测;Subbaraj P等[10]应用主成分分析提取冷却水喷雾系统中气动阀的主要特性,提高了对气动阀正常和故障状态的分类性能;刘永斌等[11]提出了一种基于主成分分析和支持向量机进行内燃机状态判别的故障诊断方法,利用主成分分析消除内燃机振动特征参数的冗余,提取反映内燃机运行状态的主成分特征,作为支持向量机的输入特征向量,结果表明该方法可以有效地识别内燃机的不同的运行的状态皮子坤等[12]针对煤矿瓦斯涌出受许多因素的影响,为了克服瓦斯涌出中存在的复杂的非线性关系,提出了PCA-MFOA-GRNN算法模型,应用PCA算法对原始数据进行降维,并降维后的结果输入模型,实验结果表明该预测模型对GRNN的参数优化后得到的预测模型较其他预测模型有更强的泛化能力和更高的预测精度。研究结果表明:该诊断方法在满足故障检测识别率的同时提高了诊断速度,为液压油缸内泄漏的故障诊断提供了一种实用方法。支持向量机在小样本条件下具有很好的泛化性能[13],能够解决实验获取的各缺陷的样本数量过少的问题,且支持向量机还具有鲁棒性能[14],能有效地避免传统统计学方法中的过学习问题、局部极小值问题、非线性问题和维数灾难问题等。

本文基于经验模态分解(EMD)[15-16]、主成分分析方法(PCA)以及支持向量机(SVM)结合的方法,实现对管道超声检测缺陷深度回波信号识别。首先,分别利用EMD对缺陷信号进行分解,对分解的各基本模式分量(IMF)分别提取其时域的无量纲参数[17],即斜度、峰度、峰值指标、清除指标、形状指标和脉冲指标;然后,采用主成分分析方法从原始特征中筛选出敏感特征;最后,用敏感特征作SVM的输入,实现管道超声波信号的识别分类。

1 超声波缺陷信号的特征提取

1.1 特征提取

经验模态分解(EMD)是一种具有自适应的时频分析方法,是分析非线性非平稳信号的有力工具。它可根据信号的局部时变特征进行自适应的时频分解,克服了传统方法中用无意义的谐波分量来表示非平稳、非线性信号的缺陷;可得到很高的时频分辨率,具有良好的时频聚集性;非常适合对非平稳信号和非线性信号进行分析。分别对深度的腐蚀缺陷超声波信号做经验模态分解,如图1所示。

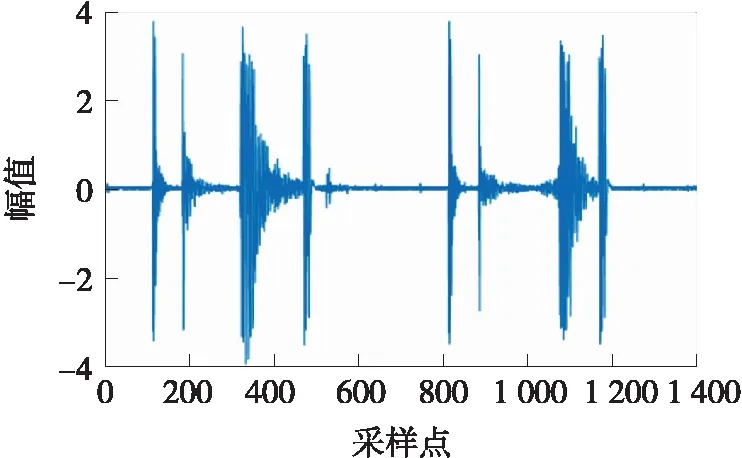
图1 局部腐蚀缺陷超声波信号图

(1)

其信号为s的标准偏差,

(2)

各时域的无量纲参数如表1所示。

对缺陷信号作EMD分解,选取占缺陷信号大部分能量的前6个IMF分量,提取各个IMF分量的6个时域无量纲参数。因此,每一个信号共有6×6=36个时域无量纲参数。

表1 时域无量纲参数

1.2 主成分分析(PCA)

设超声波腐蚀缺陷信号特征向量矩阵为X,其列向Xk=(x1k,x2k,…xnk)T为n维特征向量,缺陷的某一类型可由xk描述,xk的协方差矩阵为

(3)

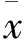
(4)

主成分通过求解协方差矩阵Rx的特征值来计算,所以应该首先求解特征值问题即:

λiqi=Rxqi

(5)

式中:λi是Rx按降序排序的特征值,qi是特征向量。

样本xi投影到特征向量qi得到该方向对应的主成分为

(6)

所有的特征向量张成一个n维正交空间,x投影到该正交空间得到相应的n维主成分。特征向量所对应的特征值越大,它在重构时的贡献也越大,特征值越小的特征向量在重构时的贡献越小。设正交空间中前m个主成分为y1,y2,…,ym,其累计方差贡献率为

(7)

当前m个主成分的累计贡献率Rm大于80%时,就可以只提取前m个主成分作为样本的特征向量。

求前m个主成分

Z=QTX

(8)

式中:Q=(q1,q2,…qm) 为每一个特征值λi相对应的特征向量;Z=(z1,z2,…,zm)为前m个主成分。

2 支持向量机(SVM)分类器设计

支持向量机SVM(Support Vector Machine)建立在统计学的VC维理论和结构化风险最小的原理基础上,在模式分类问题上具有较好的泛化性能。能够很好地解决小样本、非线性、高维数和局部极小点等实际问题。

输入两类训练样品向量(Xi,Yi)(i=1,2,…,N,X∈Rn,y∈{-1,1}),类号分别为ω1,ω2。如果Xi∈ω1,则yi=-1;Xi∈ω2,则yi=1。寻找分类超平面的问题可以转化为如下二次规划问题求解

(9)

在实际中,分类问题是非线性的,可以通过非线性变换把样本输入空间转化为某个高维空间中的线性问题,在高维空间中求最优分类超平面,这样的高维空间也称为特征空间。当在特征空间H中构造最优超平面时,训练算法仅使用空间中的点积,即<Φ(Xi),Φ(Xj)>,而没有单独的Φ(Xi)出现,使用核函数k,来表示在高维空间中的内积运算,即

k(Xi,Xj)=<Φ(Xi),Φ(Xj)>=Φ(Xi)TΦ(Xj)

(10)

则目标函数式改写成

(11)

的最优解,得到最优Lagrange乘子a*。

样本的决策函数为

(12)

(13)

输入待测样品X,根据式(11)、式(12)求解判别函数f(X),根据sgn(f(X))的值,输出类别。如果sgn(f(X))为-1,则该样品属于类ω1;如果sgn(f(X))为1,则该样品属ω2。

核函数k的不同,缺陷的分类效果也具有很大的差别,常用的核函数有线性核函数、多项式核函数和径向基核函数,描述如下:

线性核函数

(14)

多项式核函数

(15)

式中:d为多项式核函数的阶数

径向基核函数

(16)

3 超声波腐蚀缺陷检测识别系统

在腐蚀缺陷深度信号分类中,腐蚀缺陷特征可以看作是一种模式识别范式。超声波腐蚀缺陷检测识别系统包括实验数据采集和处理、基于EMD腐蚀缺陷特征计算、基于PCA腐蚀缺陷特征优化和基于支持向量机的训练与测试,如图2所示。

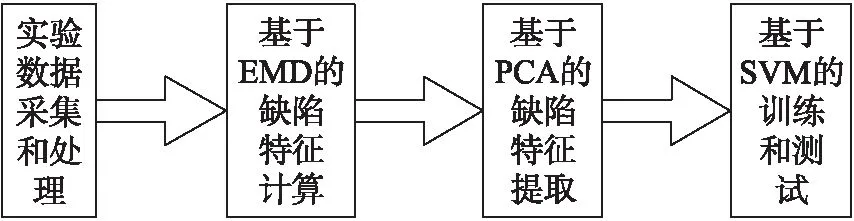
图2 流程图

超声波腐蚀缺陷检测识别系统的流程可概括为:

①实验数据采集和处理:采集表面二维尺寸同一大小,深度分别为深1 mm、3 mm、4 mm 3个局部缺陷的信号数据,并去除缺陷信号的噪声、趋势项和零均值。

②基于EMD的缺陷特征计算:将预处理好的缺陷信号作EMD分解,提取各本征模式分量的时域无量纲统计参数。

③基于PCA的缺陷特征优化:利用PCA算法提取特征,消除特征集的冗余度和降低的分类器性能的无关特征。

④基于SVM的训练和测试:对腐蚀缺陷进行了基于多类分类支持向量机的训练和测试。

3.1 实验和数据采集

试验平台由5 MHz超声波直探头,有缺陷的管道,探头前端处理电路板,RIGOL DS4024型示波器,探头线,电源,导线等构成,对含有缺陷的管道进行检测,实验装置如图3～图5所示。

图3 实验图

图4 管道缺陷图

图5 超声波探头

通过实验平台,使用超声波探头对不同深度的局部腐蚀缺陷进行检测,对每一个缺陷的检测和数据采集如表2中所示,对每个缺陷独立重复采样20次,如表2所示,分别对缺陷信号应用小波基db6作噪声去除,再去除零均值和趋势项。

表2 不同类型的缺陷

3.2 腐蚀缺陷特征计算

对预处理后的超声波信号进行EMD分解,获取6个包含超声波信号主要缺陷信息的本征模式分量。分别计算每个本征模式分量的时域无量纲统计参数,即斜度、峰度、峰值指标、清除指标、形状指标和脉冲指标,共计36维特征向量。

3.3 腐蚀缺陷特征优化

特征优化是从高维到低维空间的数据映射过程,可以避免特征维数太多,造成灾难现象。利用主成分分析可以有效地降低特征的维数和每一个特征之间的相关性。各深度缺陷的原始特征集如表3所示。

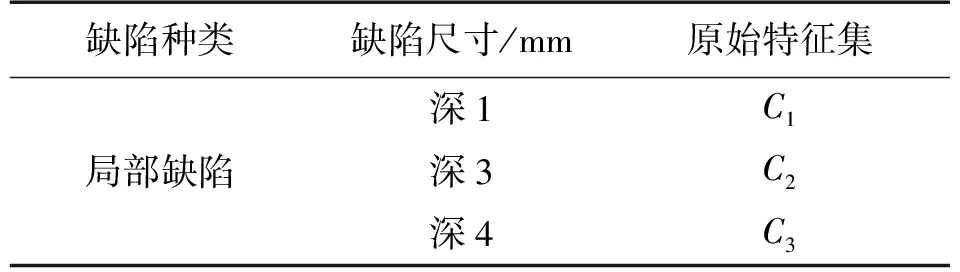
表3 不同深度的局部腐蚀缺陷的原始特征集

表3中,每一个特征矩阵的大小为20×36。PCA用于减少特征之间的相关性,并减少与缺陷相关的特征参数的维数。

为了使主成分分析能够均等对待每一个原始变量,消除由于单位不同带来的影响,将各缺陷特征集分别作标准化处理,即令

(17)

根据式(3)、式(5)、式(7),得各深度缺陷特征集的特征值、方差贡献率和累积方差贡献率。

各深度缺陷特征集的特征值如下:

局部缺陷深1 mm的特征集相关矩阵的特征值为

Λ=diag(9.97,8.45,5.16,3.39,2.29,2.15,1.34,0.96,

0.69,0.53,0.33,0.26,0.17,0.11,0.08,0.07,0.04,0.02,

0.01,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0);

局部缺陷深3 mm的特征集相关矩阵的特征值为

Λ=diag(8.86,6.5,5.56,4.54,3.27,2.41,1.31,1,0.65,

0.52,0.48,0.33,0.23,0.14,0.09,0.06,0.02,0.02,

0.01,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0);

局部缺陷深4 mm的特征集相关矩阵的特征值为

Λ=diag(8.92,6.68,5.32,3.57,3.21,2.73,1.72,1.15,

0.8,0.69,0.46,0.34,0.15,0.11,0.09,0.04,0.03,0.01,

0.01,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0);

各深度缺陷特征集的方差贡献率如图6所示。各深度缺陷特征集的方差累积贡献率如图7所示。

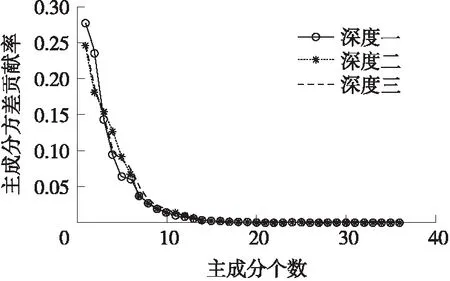
图6 主成分的方差贡献率

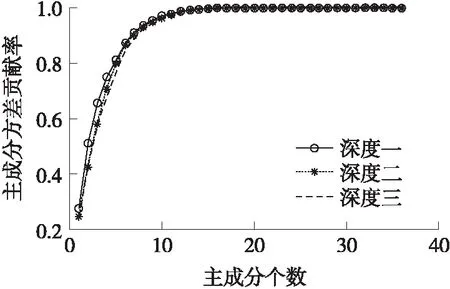
图7 主成分方差累积贡献率

从图6中可知,随着主成分个数的增加,各个主成分的方差贡献率在逐渐降低,即各主成分表征每一个深度缺陷的能力在逐渐降低,因此为保证原始样本中主要信息和避免信息的冗余,从图7中可知,当主成分的个数k=7时,每一个深度缺陷缺陷的累积贡献率都大于90%,为简化特征参数的个数,选取前7各主成分构造一个优化后的特征向量矩阵。

3.4 支持向量机的训练与缺陷模式识别

在本文中,以线性核函数、多项式核函数和径向基核函数作为支持向量机的基本核函数,在表4中,多项式核函数阶数d=1,2,3,径向基核函数的系数γ=2.17,其中,为选择不同的参数可能导致过度拟合或欠学习问题惩罚参数C和核函数系数,所以采用交叉验证方法选择。在表4中,取局部缺陷深度分别为1 mm、3 mm和4 mm的局部腐蚀缺陷作不同深度的模式识别研究。

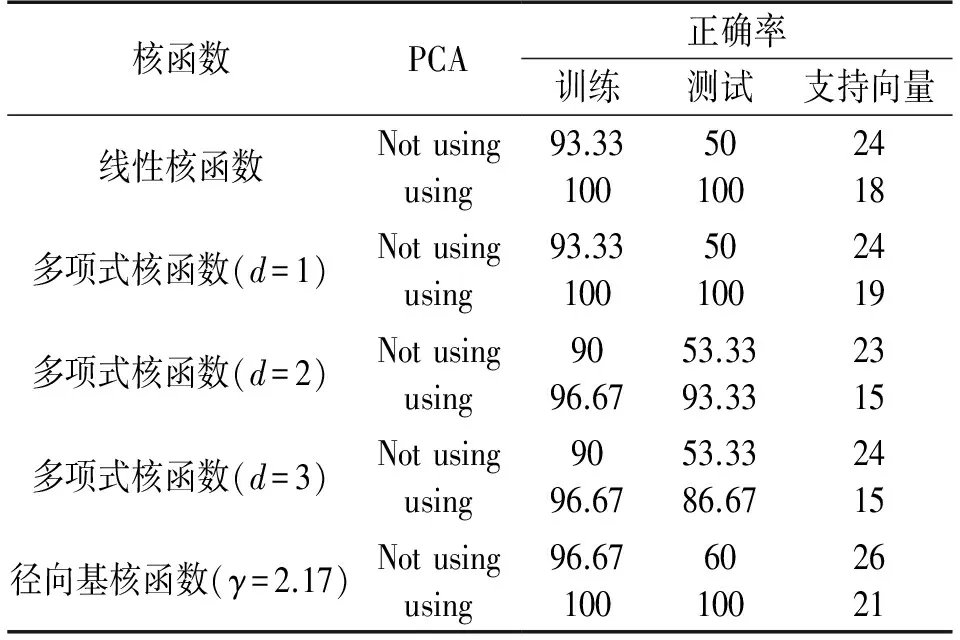
表4 基于多分类支持向量机和主成分分析的局部缺陷 不同深度缺陷的分类识别

4 结果与讨论

在表4中,我们列出了核函数、PCA、训练和测试的正确率和支持向量的个数。正确率(%)是用于训练或测试的正确分类占整个集合的比率。

4.1 特征提取效果

在表4中,用原始特征向量和经主成分分析优化后的特征向量,进行分类,分类结果如表4中所示。从表4中可以得出使用PCA提取新的特征向量的分类器的分类准确率普遍大于使用原始特征向量进行分类的准确率。没有经PCA优化的分类器的分类准确率下降的原因是由于特征集中存在的无关和无用的特征参数造成的。许多不相关的特征给分类器造成影响,往往会降低分类器的性能,采用经PCA优化后的分类器的性能优于没有经PCA优化的分类器。此外,经过PCA优化的支持向量机分类器需要的支持向量比未经PCA优化的支持向量机分类器的要少。

4.2 核函数的效果

支持向量机的性能在很大程度上取决于核函数的选择,核函数将数据从输入空间转换成高维特征空间。内核函数的选择依赖于数据,没有明确的选择规则。本文使用各种内核参数进行训练和测试。结果如表4所示,d是多项式的阶数,γ是径向基函数核函数的系数。在表4中对用PCA优化后的样本分类准确率差异不大,都得到了较高的分类准确率,但未用PCA优化的样本,分类准确率呈现出较大的差异性。在表4中,使用径向基核函数作为内核函数时,不同深度的局部缺陷的分类识别的准确率较高,且使用经PCA优化的样本进行训练测试时,均达到了100%的准确率。因此,对于不同深度的局部腐蚀缺陷的分类采用相对应分类准确率较高的径向基核函数进行分类。

5 结论

本文针对超声波腐蚀缺陷信号,提出了一种基于PCA和SVM的识别方法。该方法利用经验模态分解(EMD)提取各基本模式分量的时域无量纲参数作为原始特征,然后,利用PCA方法将高维的特征向量压缩为低维的特征向量,将得到低维特征向量输入到SVM分类器,进行不同深度腐蚀缺陷分类识别。

通过实验平台采集了不同深度的局部腐蚀缺陷超声波信号,将采集的原始信号进行预处理之后,使用经验模态分解方法分解各类缺陷信号,选取占缺陷信号大部分能量的前6个基本模式分量(IMF),并提取各个基本模式分量(IMF)的6个无量纲时域参数,共计36个特征,经过主成分分析后得到4个经PCA优化的低维特征向量。将36个初始特征和7个新的特征分作为分类训练样本,分别选择线性核函数、多项式核函数和径向基核函数构造支持向量机分类器,对腐蚀缺陷特征进行训练测试。通过对比选择适合腐蚀缺陷信号的核函数与相关参数,实现腐蚀缺陷深度的分类。结果显示,采用PCA的特征提取方法有效地提高了缺陷深度的分类正确率。