传感器网络中阈值Nesterov加速梯度下降定位方法*

秦宁宁,陈 肯,孙文心(江南大学轻工过程先进控制教育部重点实验室,江苏 无锡 214122)

无线传感器网络技术的快速发展对基站的定位精度和定位效率提出了更高的要求。基于测距的定位算法相对于非测距的定位算法[1],有着更高的定位精度[2]。作为间接测距的代表,RSSI定位算法,由于不依赖于外设硬件的易于实现性,促使其成为了研究的热点。但另一方面,受无线信号强度易扰特性的影响[3],其量测过程中的不稳定性,也会导致测距存在误差,进而影响定位精度。

为平衡RSSI信号的不确定性引发的定位偏差问题,通常从数据预处理与定位求解2个方面着手解决[4]。在预处理环节中,通常采用增加信道参数的测量频次、利用滤波器对RSSI数据进行前置处理[5],或者对信号传输模型进行高斯拟合[6]等方法来提高模型精度,从而达到精确距离估计的目的。

而在定位求解的过程中,对于参考基站较少的传感器网络,极大似然估计技术[7]可以被用来求解联立方程中的未知基站坐标。恰如文献[8]给出的一种基于最大似然求解的定位算法,利用两次加权最小二乘法,获得了更为精确的定位坐标,但其未考虑信道模型的衰减系数对信号传输距离的影响,过分依赖先验知识来减小测量误差。针对环境因素考虑的缺失问题,一种基于RSSI的加权概率定位算法[9]被提出,在一定程度上强调了环境对定位模型的影响,但存在环境参数一旦确定就不再调整的弊端,因此该算法并不能很好地克服通信环境的不稳定性,对定位精度的改善也不明显。

虽然可以通过增加参考基站,提高定位精度,但随着基站数的增加,基站与基站间的RSSI值的误差积累,也会降低未知基站的定位精度。因此,在多基站的大型传感器网络中,通常使用群智能的寻优策略,解决未知基站坐标的求解问题。

文献[10]就曾基于RSSI信息,提出了一种基于粒子群PSO(Particle Swarm Optimization)的定位算法,利用对数障碍函数对目标函数进行改进,但该方法容易陷入局部最优且必须以未知基站的邻站作为必要的参考信息。针对以上问题,冯秀芳等人提出了一种分步粒子群IPSO(Split-step Particle Swarm Optimization)的定位算法[11],一定程度上避免了局部最优的情况,但数据处理量会出现陡增现象,很难满足定位的实时性需求。针对多数算法寻优速度慢的问题,文献[12]提出了基于链路质量指示LQI(Link Quality Indicator)的RSSI测距方法,利用硬件提高了测距精度的同时,改进了粒子群算法寻优精度,但未考虑信道衰减系数变化对量测距离的影响。

综上,论文以参考基站的RSSI信息为基础,在传感器网络的定位过程中,同时兼顾精度与求解效率,提出了一种阈值Nesterov加速梯度下降定位方法NAGT(Nesterov Accelerated Gradient Descent with Threshold)。新方法将每个参考基站的RSSI量测信息等效为单次梯度,通过更新寻优动量,加速收敛速度并提高寻优精度,增加损失函数阈值环节以降低陷入局部最优的风险概率,从而在优化定位精度的同时,也保证了求解速率。

1 系统模型

1.1 通信模型

无线通信中普遍采用的基本的信号传输模型如式(1)所示[4]

Pr(d)=P0-10αlog(d/d0)+Xσ

(1)

式中:Pr(d)为基站对距离d处的接收信号强度,P0为基站对参考距离d0处接收信号强度,α为信号衰减系数,Xσ是服从N(0,σ2)分布的高斯白噪声。

(2)

可得Pri亦服从高斯过程分布,其概率密度函数为

(3)

利用Xσi的对称特性,得:

(4)

因此,对于N个已知基站Basei而言,存在关于参数θ=(x,y,P0,α)的最大似然函数,如式(5)所示:

(5)

(6)

式中:

(7)

1.2 多约束目标函数转化

鉴于直接求解形如式(6)的多约束最优化问题十分困难的情况,受文献[10]的启发,引入对数障碍函数将多约束目标函数转化成无约束函数。其中,对数障碍函数的一般通用形式如下:

(8)

式中:μ为障碍变量,ci(z)≥0,ci(z)=|θ-θbound|,θbound为所求参数θ的各分量的取值边界,可以将式(6)中的约束条件转化为:

μ[ln(P0-P0min)+ln(P0max-P0)+ln(α-αmin)+
ln(αmax-α)+ln(x/d0)-(xmin/d0)+ln(xmax/d0-x/d0)+
ln(y/d0-ymin/d0)+ln(ymax/d0-y/d0)]

(9)

的表现形式。

需要说明的是,观察式(7)可以发现,由于P0和α不包含于log(·)内,因此P0和α的微量扰动会对目标函数f产生较大的波动影响,不利于定位精度的提高。而利用式(9)的障碍函数变形,重新规划变量的表达,从形式上一定程度地抑制了P0和α的扰动引发大误差的现象。

基于上述推演分析,将式(7)与式(9)结合,式(6)可以更新表达为式(10)

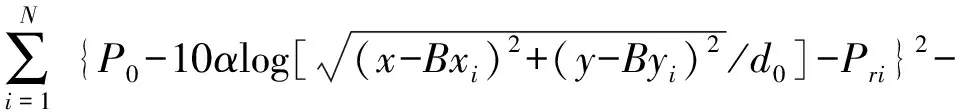
(10)

至此关于式(6)的多约束定位求解问题已经规划为无约束寻优问题,使得利用NAGT方法成为可能。

2 NAGT算法

在信道环境参数未知,已知N个基站Basei的网络中,解决1个未知基站UBase的多约束定位求解问题,在规划成式(10)的基础上,可将定位过程中基站增加等效为梯度迭代中时间的递增,利用基本NAG的迭代原理,在不断的更新寻优过程中,实现对新目标函数式(10)的求参。

2.1 基本NAG基本原理

Nesterov加速梯度下降法(Nesterov Accelerated Gradient Descent NAG)在随机梯度下降法SGD(Stochastic Parallel Gradient Descent)的基础上,通过结合动量法思想,优化了寻优效率。

NAG方法的基本迭代公式如下式所示:

vt=γvt-1+ηθJ(θt-1-γvt-1)

(11)

θt=θt-1-vt

(12)

式中:第t时刻的动量vt,动量项γ,θJ(θt-1-γvt-1)为损失函数J关于θt-1的梯度,η为步长,θt为所求当前t时刻的参数。各变量之间的寻优关系,如图1所示。

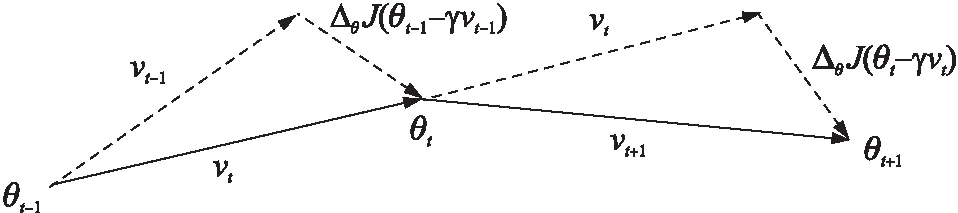
图1 NAG寻优中的变量关系图

2.2 梯度等效

为构建N个基站之间的迭代关系,基本NAGT将第i个基站对应于式(11)中的t时刻,遍历每个已知基站来更新动量及参数来达到定位误差最小。鉴于式(10)是包含N个基站信息的整体目标函数,为每个独立基站Basei定义损失函数ei作为独立目标函数,以力求尽可能无损地等效整体目标函数。

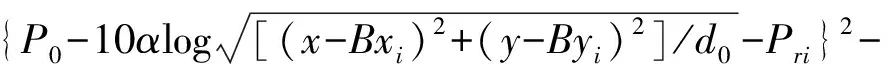
(13)

2.3 损失限制阈值

为克服迭代算法中出现的局部最优的痼疾,NAGT增设单基站的损失函数的阈值bth与所有基站累积阈值Bth,分别控制某个基站的损失或所有基站的累计损失过大,避免算法陷入局部最优。即应确保下式成立:

(14)

(15)

2.4 算法流程

通过梯度等效步骤,可以利用提出的NAGT算法来获取UBase坐标。NAGT算法的基本步骤如下:

步骤1 初始化 设置θ0,γ,η,v0=0,j=1,迭代监测间隔kth与迭代上限Kth;获取N个Basei坐标(xi,yi),及其与UBase间的Pri,i=1,2,3,…,N;

步骤2i=1;

步骤3 计算vi,θi,ei,i+1→i;

步骤4 若i≤N,返回步骤3;

步骤5j+1→j,vN→v0,θN→θ0;

步骤6 若j≥Kth,则进入步骤9;

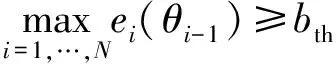
步骤8 返回步骤2;

步骤9 输出参数θN,退出。

考虑到NAGT算法本身对θ0=(x0,y0,P0,α)的不敏感特性,因此根据式(6)的约束条件,随机设置θ0的取值。

算法中,步骤3～步骤4完成了对所有已知基站Basei的遍历,等效为梯度的递推寻优过程;步骤5～步骤7中,通过限制ei(θ;xi,yi,Pri)的大小以达到控制局部最优的目的。因此,设置迭代监测间隔kth,定时检测并避免算法陷入局部最优。纵观步骤2～步骤8,算法将每j轮遍历基站得到的最优值,作为下一轮寻优的初始值,保证了迭代的连续性,有利于提高结果的准确性。

3 仿真实验

为了验证定位算法的性能,实验采用MATLAB仿真平台,场景设置为100 m×100 m的正方形区域,UBase(xu,yu)的真实坐标不作特殊说明时为(50,50),已知基站Basei位置随机设定,且彼此间能保证正常的信号通信。结合文献[14]和实验测试,仿真参数设置如下:γ=0.9;η=0.001;阈值设置bth=6,Bth=10;μ=5;kth=50;Kth=200;P0min=-25 dB,P0max=-50 dB;αmin=1;αmax=6;xmin=ymin=0;xmax=ymax=100。

实验将论文提出的NAGT算法与以NAG、 SGD和PSO为寻优核心的定位算法,进行定位性能的对比。在仿真实验中,为降低PSO陷入局部最优的概率,将其搜索粒子数设为100,粒子的个体最优权重系数设置为c1=1,群体最优值的权重系数设置为c2=4,惯性权重设置为w=0.8[10]。

3.1 定位精度分析

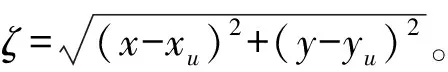
通过图2所示的定位误差分布箱式图,可以看出:无论是从误差中值、误差分布的范围,还是异常点数目分析,和其他3种算法相比,论文给出NAGT方法,具有分布集中且最小的定位误差,同时定位偏失引发的误差异常情况也最为稀少。这是由于,NAGT在寻优过程中,不断利用动量对上一时刻获得的参数进行修正,提高了寻优精度与定位精度。

图2 4种算法定位误差分布比较

PSO算法通过空间中的粒子寻优,定位精度虽不及NAGT,但也表现良好。NAG算法由于没有添加阈值对定位损失函数进行限制,因此精度尚不如PSO。SGD由于更侧重于提高寻优的速率,降低计算机的运算负载,忽略了寻优的精度,因此在4种算法比较中,定位精度最低。

3.2 对基站数的敏感性

虽然基站数目N的增长对于定位精度的提升有着正向激励,但不同机理驱动下的算法受N的影响程度和范围也不尽相同。因此,本实验分析了4种算法中,基站数目N对定位精度的影响情况。设定6个不同基站数目的实验场景,N=5,10,15,20,25,30,4种算法分别对每个场景进行1 000次仿真,通过对其平均定位误差的比较,分析不同算法对基站数目的敏感性,仿真数据分析结果如图3所示。

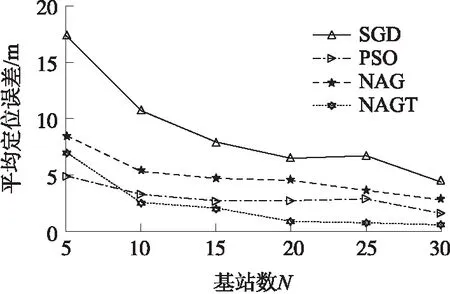
图3 基站数N对各算法影响示意图

实验中,可以看出4种算法的定位精度均随着基站数目N的增加有所提高,在数据曲线上体现为平均定位误差的下降。这种下降的趋势在N<10的小规模网络中更为陡峭,但随着N的增加,对于减少定位误差的贡献,逐渐减缓。相比其他3种算法,NAGT在多数实验场景中,具有最小的平均定位误差。

需要说明的是,由于PSO的定位机理是将所有基站列入寻优的目标函数,因此在N<10的小规模场景中,PSO算法相比于其他3种算法具有更小的平均定位误差。但随着N的增加(N≥10)对定位误差的贡献减少,PSO算法的优势减缓,而基于自适应调节动量为核心的NAGT算法优势凸显,其平均定位误差基本保持在1 m～2 m微小区间内。

3.3 定位速率的比较

若以定位过程的时长作为定位速率的考量,在N=20个Basei的场景中,针对同一UBase,对3种算法(NAGT,PSO和SGD)进行1 000次定位,并计算平均单次定位时长,计算数据如表1所示。

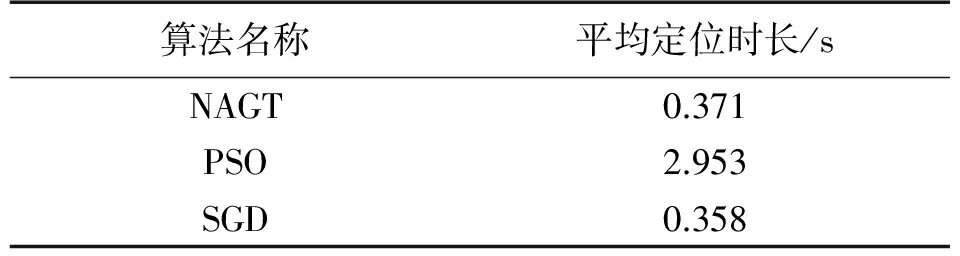
表1 3种算法定位时长对比表

3种算法中,SGD和NAGT法的定位速度相对较快,时长控制在0.4 s之内,PSO定位速率最差,平均定位耗时接近3 s。PSO方法在寻优过程中需要并行处理所有Basei坐标,而基于梯度思想的NAGT和SGD,在寻优过程中每次迭代,只需利用一个Basei坐标信息,因此计算负荷较小。可见,NAGT在保证定位精度的同时,也能将定位速率稳定在较高的算法水平上,体现了NAGT方法的实用价值。

3.4 未知基站坐标对精度影响

本实验通过对UBase 位于不同位置的定位误差测试,考量4种算法定位精度对UBase 位置的敏感程度。分别设定UBase 位于区域对角线上11个不同位置,以UBasei(xu,i,yu,i),i=1,2,…,11进行标识,其中xu,i=yu,i=10·(i-1)。基于上述11个位置场景,分别对N=20个随机分布的已知基站进行 1 000 次重复实验,实验数据为平均定位误差,实验数据分析结果如图4所示。

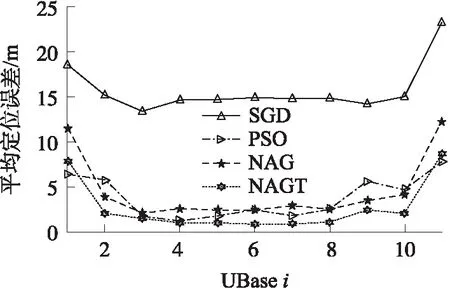
图4 不同UBase 对定位误差的影响分析

从图4曲线的整体分布和趋势可以看出,NAGT的定位精度优于其他3种算法,PSO与NAG的性能基本相当,而SGD因为具有超过15 m的平均定位误差,定位精度最差。当UBasei位于区域中心地带(即i=2,3,…,10)时,4种算法的平均定位误差均能稳定在各自较低的误差范围内。相对于其他算法,论文提出的NAGT,具有最小的平均定位误差,即定位误差稳定在1 m左右。

当UBasei位于区域角落,即i=1,11时,由于自身位置较为偏远,因此接收到的RSSI信号衰减相对严重,4种算法的平均定位误差均均呈现出陡升增长。且相对于同时利用所有Basei信息的PSO方法,NAGT算法对于信号衰减所受不良的影响略微明显,因此在UBasei位于边界附近时,会出现短暂的定位误差略高于PSO的现象。

4 总结

基于RSSI的定位算法虽然有精度相对较高,所需硬件成本低的定位优势,但因通信模型易扰性使其应用具有很大的局限性[15]。针对上述缺陷,论文将包含信道衰减系数范围的对数障碍函数进行拆分,利用 NAGT方法进行迭代寻优,在保证定位速率的情况下,得到了更加准确的定位结果。

虽然NAGT方法解决了一般智能算法定位速率慢、定位精度相对较低的问题,但存在寻优结果易陷入局部最优导致定位误差大、小型传感器网络定位精度较低的缺陷。因此,提高RSSI定位模型精度和降低局部最优概率也将被作为未来提升NAGT定位方法的有效途径,以此开展进一步的研究。