在观察、操作、想象中自主发展空间思维能力
——《长方体的认识》中怎样落实核心素养
(湖北省宜昌市点军区点军小学 湖北宜昌 443004)
数学核心素养是学生数学素养的重要标志、体现数学课程的基本理念和总体目标、反映了数学的本质和价值。那么我们在课堂中该如何落实呢?下面就以《长方体的认识》为例谈谈我的做法。
一、从学生已有的知识经验出发,感知点、线、面的空间关系
课始提出问题:生活中那些物体是长方体?观察你手中的长方体实物,说一说长方体都有哪些部分组成?各部分叫什么名称?

然后让孩子们组内互相指一指长方体和正方体的面、棱、顶点。
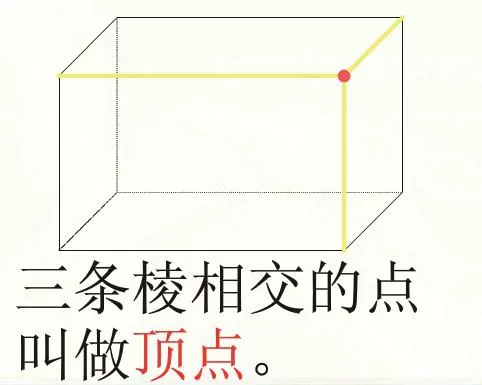
像这样从孩子们最熟悉的长方体的面开始,引导学生观察发现面与面相交成一条直线段即为长方体的“棱”,三条棱相较于一点即为长方体的“顶点” ,由“面——线——点”来感知长方体上点、线、面的空间关系。
二、通过有序的观察、操作帮助学生建立长方体的空间立体感
课的第二个环节便是按照下面的顺序探索长(正)方体的定点、棱、面的特点。
1.数一数看看长(正)方体各有几个顶点,几条棱,几个面?
2.通过量一量,比一比,看看哪些面大小相等?哪些棱长度相等?
(1).小组议一议,将长方体和正方体的特点填写在下面的表格里:
(2).全班分享长(正)方体的特点(依据表格进行汇报分享,边操作边分享,做到有理有据,互动充分。老师注意适当介入,抓住重难点。)
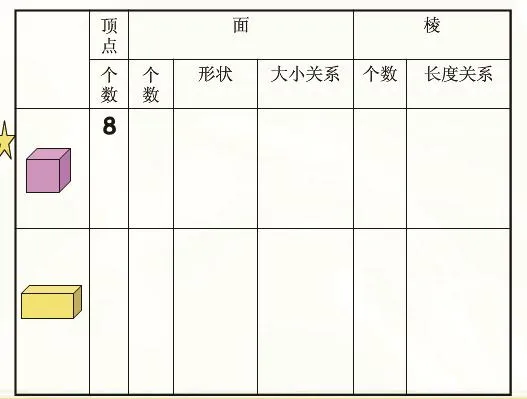
在分享环节中我介入两次。一次是孩子们在介绍面的个数时,问孩子们:“能否用一个带有方向的字来说一说长方体都有那几个面? ”孩子们很快就想到了用“上、下、前、后、左、右”这六个方向来给面命名。还一次就是孩子们在数“棱”时总是很容易数重复或数掉,因此我顺势提问:“有没有什么好的办法在数的时候做到不重复又不遗漏,而且又很有序?”这一问题开始还是难倒了孩子们,最后经过小组讨论还是得出了方法。记得很清楚,孩子们是这样说的:“我们发现这些棱都有方向的,一种是从左往右的棱(其实就是横向的)由4条而且相等;一种是从前往后的棱(就是纵向的)也有4条,也相等; 还一种就是从上到下的棱(就是竖向的) 也是4条,也相等。我们在数的时候一个方向一个方向的数就不会数错了。” 说完后紧接着就让孩子们手拿长方体按照这样的方式数数看,看是不是这样的?数完后之前不太相信的孩子在嘴里嘀咕着:还真是这样!这个方法好!
其实基本特点完全可以通过直观操作得出。关键是要引导孩子们通过有序的数面和棱来感知长方体的顶点、棱、面三者自身的摆放位置,以及三者之间的位置结构,特别是棱的方向性,是一个难点,同时也是重点,通过对它的突破。可以很好地让孩子深刻感知长方体的三维立体空间感,从而培养孩子们有序的空间思维能力。
三、通过“想象”来培养学生的空间思维能力
明确了长方体的特点以后,紧接着按照下面的步骤和孩子们进行一个想象的游戏:
1.出示一个点“.”,让孩子想象长方体的样子…(孩子们都说想象不出来)
2.紧接着从这一点引出一条棱,让孩子想象长方体的样子…(孩子们说还是想象不出来它的样子)
3.再接着从这一点引出另外一条棱,让学生想象长方体的样子…(孩子们忧郁的说好像还是不能想象出来,但是我可以想象到一个面,也有孩子说,我大概可以知道这个长方体由多长,有多厚了。)
4.最后从这一点引出第三条棱,让学生想象长方体的样子…(大多数孩子表示能想象出来这个长方体是什么样子了。)
5、那是什么样子呢?为什么我从一点引出了三条棱你才能想象出来呢?孩子们有的是将这个长方体画出来后 加以说明,有的是利用每两条棱确定一个面的大小的方式说明的,我觉得说的最好的便是:只有有了这三条棱我们才知道这个长方体有多长(横向),有多宽(纵向),有多高(竖向)。因为这样我便可以水到渠成的告诉孩子们“你们真棒!”其实能确定长方体形状和大小的三条棱分别叫做长方体的长、宽、高。即相交到同一顶点的三条棱分别叫做长方体的长、宽、高。习惯上我们将横向的叫做长,纵向的叫做宽、竖向的叫做高。
这样由点到线,再从线到面,再从面到体,即从一维,到二维,再到三维,很好的再次建立点、线、面的空间关系,孩子们对长方体的那种空间感便越来越清晰了,其空间思维能力得到了很好的发展。
纵观全课,我主要通过从孩子已有知识经验出发,借助实物发现并归纳长(正)方体的特点,并通过有序的操作展示,想象说理来理解其特点,让孩子们在有序的观察、操作、想象中感知“点(顶点)——线(棱)——面”的空间关系,较好的培养了孩子们的数学核心素养——“空间思维能力”。

