基于初中数学逆向思维教学的探索
(吉林省长春市第五十三中学 吉林长春 130000)
一、课堂中穿插逆向思维的故事
初中生一个明显的身心特点就是情感丰富,很容易受到老师的影响。作为一名初中数学教师,应该时常注重学生思维方式的锻炼。因此,笔者在课堂上经常穿插一些逆向思维的小故事,看看故事的主人公在遇到问题,遇到困难时,他们如何想的又是如何做的。通过故事来激发学生的创新欲望。例如,在课堂上我会说一些幽默的故事:
故事一:古代有一个土豪,每次出门都担心家中财物被盗,于是想买只大狼狗给看家护院,但又不想浪费银两。埋头苦思许久后,得一妙计:每次出门前把wif i 修改成无密码,然后放心出门。(此处学生大笑,这一笑说明学生已经跟上你的授课内容)每次回来都能看到十几个人捧着手机蹲在自家门口,从此土豪无忧。从土豪的故事我们得出一个结论:看家护院,不一定要养狗。虽然看似无稽之谈的故事,却隐藏了一些思维问题,提醒我们大家在以后的生活和学习中,换个角度想问题,结果会大不同。
故事二:一位大爷到菜市场买菜,挑了3个西红柿放到秤盘,摊主秤了下,说到:“一斤半3块7。”大爷说到:“做汤不用那么多。”去掉了最大的西红柿。摊主道:“一斤二两,3块。”正当身边的人要提醒大爷注意摊主的秤时,却见大爷很从容的掏出了七毛钱,拿起刚刚被摊主去掉的那个大的西红柿,潇洒地走开了。其实在生活中,或者更具体一点,在我们数学学习中,有时候你换一种思维方法,你就会发现解决问题的另一个方法,而这种方法却更为简洁。
二、课堂中增加公式或法则、定理的逆用
1.合理逆用公式或法则
初中数学中公式或法则的对于学生来说,理解起来相对比较容易,但很多学生由于思维定式,仅仅习惯于从左到右运用公式或法则,而对于从右到左的逆向思维却不习惯。因此,在课堂教学中,我会有意识的增加一些公式或反之则的逆用,以此来拓展学生的思维方式。
例如:
(1)同底数幂的乘法法则
同底数幂相乘,底数不变,指数相加,即am·an=am+n(m,n是正整数)。
(2)幂的乘方公式
底数不变,指数相乘,即(am)n=amn
课堂上我给出am+n=am·an(m,n是正整数)和amn=(am)n。而且在做练习题的时候,我会有意识的增加这方面的联系。下面就是我给出的练习题:
已知am=2,an=3,求a3m+2n的值。
在这个练习题中我已知的条件是am和an,却没有a3m和a2n。这个时候,我就提示同学们可以用故事中土豪或者老大爷的思维方式,我们逆向思维,从所求结果推向已知条件。首先,a3m+2n用到同底数幂相乘的逆向法则,可以写成a3m+2n=a3m·a2n,然后用到幂的乘方公式的逆法则,即a3m=(am)3,a2n=(an)2,如此一来,很容易求得结果。
解:a3m+2n=a3m·a2n=(am)3·(an)2=23·32=27
2.慎重运用逆向定理
作为初中数学教师,经常会给学生强调:一个命题成立,但它的逆命题不一定正确。但是又要告诉学生不要误解我的这句话,定理的逆用还是可以的。因此,课堂上我也会经常拿出解决问题的一种办法------分析综合法,也就提醒学生要逆向推理,从题目要你证明的结论出发往回推理。
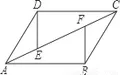
练习题:如图,在平行四边形ABCD中,E、F是AC上的两点,且AE=CF.求证:DE=BF。
正向思维(由因求果):
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD,AD=BC,AD∥BC
所得结论哪些要用,哪些没用,对于数学学习处于中下层次的学生来说的确不是一件容易的事情。
逆向思维(由果索因):
欲证DE=BF
则要证明△ADE≌△CBF(更简单)或△CDE≌△ABF
而要证明两个三角形全等,则会想到我们学过的定理有角边角,边角边等,因此要证明△ADE≌△CBF我们可以用到边角边定理,∠DAE=∠BCF,[AD=BC],AE=CF,三个条件中由一个已知的条件即AE=CF,另外两个条件则由四边形ABCD是平行四边形的性质得出至此,解题思路清晰的呈现出来。
通过该练习,我会告诉学生有时候使用逆向思维来解题,你的解题方向会更明确,解题思路会更清晰,可以避免写出一些无用结论,浪费时间。同时,我和学生们一起总结:解题中首先要看题目中的结论是要证明角相等,还是边相等或其他等等,如果要证明角相等,则常用的方法有(1.对顶角相等2.平行线里同位角相等、内错角相等3.余角、补角定理4.角平分线定义5.等腰三角形6.全等三角形的对应角等),然后结合题意中的已知条件,选出其中的一种方法,然后再考虑用这种方法证明还缺少哪些条件,把题目转换成证明其他的结论,通常缺少的条件会在第三步引申出的条件和题目中出现,这时再把这些条件综合在一起,很条理的写出证明过程。
3.精心设计课后练习题
除了课堂上注重学生逆向思维的锻炼,还要在课后将这种思维方式进行延伸。因此,在课后练习题的布置上,我会精心设计,让学生既考虑正向思维,又考虑逆向思维,还要考虑两者的综合应用。
三、让学生生活中的常识跟数学学习联系起来
在我们的生活中有很多初中数学的实例,例如商品降价问题:某商品进价是1000元,售价是1500元。由于销售情况不好,商店决定降价出售,但又要保证利润为5% ,求商店应降价多少元出售。再比如:存款利率问题:国家规定存款利息的纳税办法是:利息税=利息×20% ,储户取款时由银行代扣代收。若银行一年定期储蓄的年利率为2.25% ,某储户取出一年到期的本金及利息时,扣除了利息税36元,则银行向该储户支付的现金是多少元?像这样的例子还有很多,诸如打车的费用计算问题,股票的计算问题等等。所以,在课堂上举例时,通常会用生活中学生经常接触的,让他们很自然的将知识进行迁移,同时也提高学生学习兴趣,让他们自主的进行数学探索,为改进思维方式,提高创新思维提供可能。
总之,各位同仁应不断更新教育理念,努力学习先进的教学方法,在深刻领会教学大纲的基础上,深入钻研教材,以此培养学生的创新思维。

