“原创”显身手 “研发”呈佳品
山东 尹承利
由《教学考试》杂志社主办的原创研发项目,通过原创团队教师的通力合作,呈现在大家面前的是一套可谓上乘的原创试卷.我作为亲身经历者,与“原创”“研发”一同成长,感同身受!故将参与此次活动的体会和感想付诸文字以飨各位同仁.
一、活动安排组织井然
此次原创活动《教学考试》杂志社精心安排、组织,一环扣一环,从原创团队活动安排的流程图便可窥见一斑,而且在每一个时间节点都公布各团队的进度,并指导下一步的工作.首先两位命题老师初拟原创卷考点细目表,敲定后又不辞辛劳地命制试题,并通过在线试题优化、在线试题解读等教研活动,团队老师们对整套试卷的考点设置和分布,乃至每道题的设问方式都畅所欲言、反复推敲,最终呈现出一套成功、漂亮、经得起检验的精品试卷.
二、突出原创把握动向
“原创”是此次活动的主旋律,两位命题老师不落窠臼,在“原创”方面下了很大的功夫,保证了整套试卷的原创性.与此同时,突出“原创”又紧紧把握高考命题动向和趋势,整套试卷至少体现出了以下特点:
1.强化重点、热点
原创卷强化了对重点内容的考查,函数与导数、三角函数与解三角形、数列、空间向量与立体几何、圆锥曲线、概率统计等传统意义上主干知识在客观题和解答题中都进行了考查,构成试卷的主体内容.特别值得肯定的是,“数学文化”作为高考考查的热点,在原创卷中得到了有益的尝试和探索,体现了高考“增加数学文化”的要求.
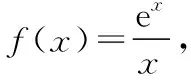
( )
A.f(x)的图象关于原点对称
B.f(x)的图象关于y轴对称
C.f(x)在(0,1)上单调递增
D.f(x)在(0,1)上单调递减
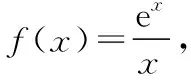
【点评】函数的概念和性质是贯穿高中数学的重点内容,导数是解决函数问题的有力工具,本题为此作了积极的考查.奇偶性判断可用奇偶性规律;单调性判断可以用导数来分析.
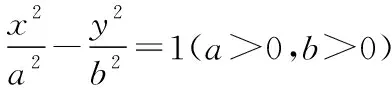
( )
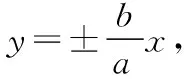
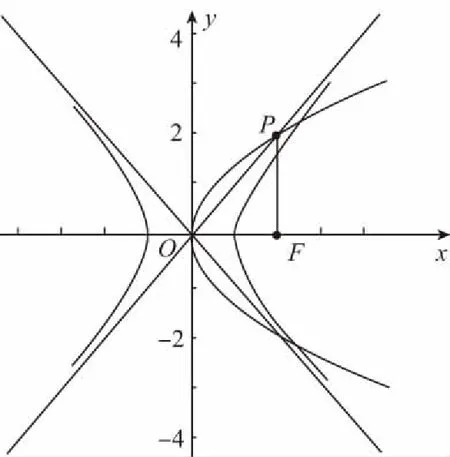
【点评】双曲线和抛物线是历年高考在客观题中考查的重点和热点.本题考查了双曲线和抛物线的几何性质,以及直线与圆锥曲线的位置关系.
示例3.(原创卷文9)如图,正三角形ABC内的图形来自中国古代的太极图.正三角形内切圆中的黑色部分和白色部分关于正三角形的中心成中心对称.在正三角形内随机取一点,则此点取自黑色部分的概率是
( )
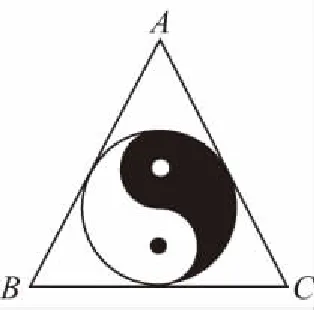

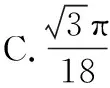
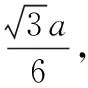
【点评】数学文化是数学学科的一个有机组成部分,有着非常丰富的内涵和外延.在数学高考中对于数学文化的考查,旨在发挥高考“指挥棒”的作用,通过考题让学生感受中国的传统文化之美并予以传承.本题改编于2017年高考全国一卷文4、理2题,主要考查数学传统文化及几何概型.在我国传统文化中有很多体现“数学美”的图形.如本题所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互转化、对称统一的形式美、和谐美.
2.考查基础不放松
原创卷加强对基础知识、基本方法的考查,试题从考生熟悉的基础知识入手,无论是必修内容,还是选修内容,许多试题大都属于常规题.集合、复数、常用逻辑、线性规划、向量、算法程序框图、排列组合等内容在选择、填空题中得到了有效的考查.尤为指出的是,部分题目“源于教材,高于教材”,做足了教材文章.如原创卷理6就是源于人教A版选修2-3第75页习题2.4 A组第2题变形的一道考题,原创卷理13就是源于人教A版选修2-1第25页例4.(1)变形的一道考题,原创卷文、理7就是源于人教A版必修5第91页练习1.(2)变形的一道典型考题,这对正确地引导中学数学教学都起到良好的促进作用.因此,在复习备考中,要再次回到课本,把课本上的有关内容弄懂,对课本中的典型例、习题做到心中有数,对课本中的典型证明做到熟练掌握.对课本典型例、习题通过仿造变式、反向变式,保留条件、引申结论,变更条件、推出新的结论等途径,从不同的角度进行研究,从而落实基础,总结解题规律.
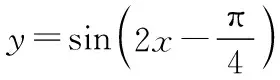
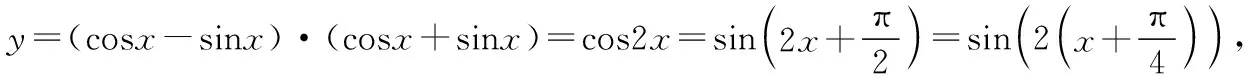
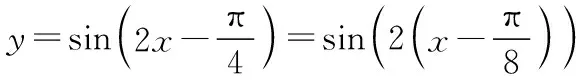
【点评】本题改编于人教A版必修四第55页练习 1.(1),考查三角恒等变换和三角函数图象的平移变换.在三角函数的图象变换中,无论是“先平移后伸缩”,还是“先伸缩后平移”,均需记清每次变换是对x而言.根植于课本是高考命题的原则和方向,值得同学们复习备考时特别关注.
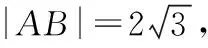
( )
A.x=1 B.y=-x+1
C.y=x+1 D.y=1
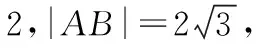
【点评】本题改编于人教A版必修二第127页的例2,考查了点到直线的距离公式、垂径定理的应用和直线与圆的位置关系.
3.知识覆盖合理
原创卷一个最为显著的特点是不回避冷点,知识覆盖面全面、合理.对一些“冷点”知识的考查在原创卷中初露端倪.比如,原创卷理6考查的是正态分布、理8考查的是线性回归分析,原创卷文15考查的是推理、文18(2)考查了点到平面的距离的求法、文19考查了独立性检验等.由此启示我们,在复习备考的过程中,要全面复习,不放弃、不冷落任何一个知识点.
示例6.(原创卷文15)三位地质学家到沙漠进行考察,每人身上最多可以携带供一人在沙漠生存16天所需的食物和水,计划每天向沙漠深处走20公里,每人可以将部分食物和水交给其他人然后独自返回,若要保证三人能安全返回,则此次考察最远可以深入沙漠________公里.
【解析】不妨设甲最先返回,丙最后返回;如果人员安全返回后,剩下人员尽可能满载则可最远.由此可知行走4天后,甲留4天的食物和水,将剩下的8天食物和水平分给乙和丙,这样甲可以安全返回,且乙和丙仍各保持16天的食物和水的满负荷状态;再行走4天后,乙留8天的食物和水,将剩下的4天的食物和水给丙,这样乙可以安全返回,且丙保持16天的食物和水的满负荷状态;然后丙可以行走4天后再安全返回,这样丙共行走12天,最远可以深入沙漠240公里.
【点评】本题考查逻辑推理能力.以逻辑推理问题命制高考题,既能创造宽松又竞争的环境,拉近考生与数学的心理距离,又能考查学生的阅读理解能力和逻辑推理能力.乍看这类问题,高中所学的知识好像在此全无用武之地,练就百遍的解题技巧似乎也在此搁浅,然而数学思维能力,却在此大放光彩.
示例7.(原创卷理8)据统计表明,某城市每月的雾霾天数与该城市每月里的汽车出行量呈线性相关关系,已知该城市10-12月份的数据统计如下表:
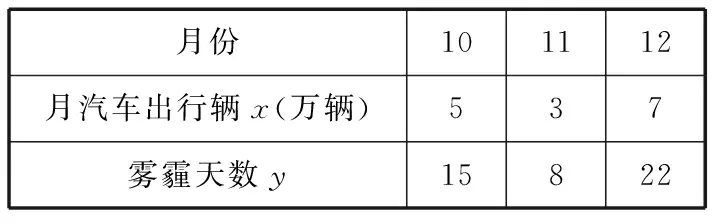
月份101112月汽车出行辆x(万辆)537雾霾天数y15822
要使下一年元月份的雾霾天数不超过11.5天,那么该月里汽车的出行量应控制在( )万辆以内.
A.4 B.5
C.6 D.7
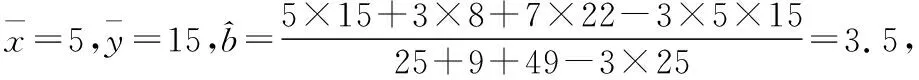
【点评】本题考查了回归分析的基本思想及其初步应用、回归直线的意义和求法、数据处理的基本方法和能力.考查运用统计知识解决简单实际应用问题的能力.
4.能力立意突出
原创卷命题突出能力立意,注重考查知识间的内在联系,在知识点的交汇处设计试题,重视对考生的创新意识的考查,注重对未来继续学习的能力考查.新情景创新题(比如,原创卷文11、19,原创卷理5、11、17等)、知识交汇题(比如,原创卷文13、文理12、文理16、文理21、22等)比比皆是.
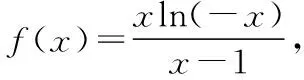
( )
A.1个 B.2个
C.3个 D.4个
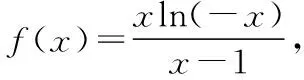
【点评】本题考查函数奇偶性、导数与函数的单调性、函数与方程等知识,难度较大,得出f(a)=a是解答本题的关键,再由函数是奇函数,进而确定最终的答案.
示例9.(原创卷文理16)已知a=(2,0),b=(1,1),c=λa+(1-λ)b,λ为非负实数,则向量a,c夹角为θ,则θ取值的范围为________.
【解析】由题意可知,
c=λa+(1-λ)b=(1+λ,1-λ),a·c=2(1+λ),λ≥0,

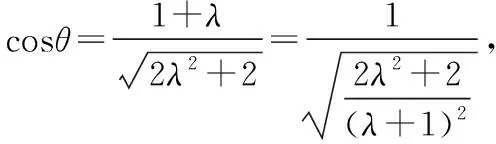

因为λ≥0所以t∈(0,1],
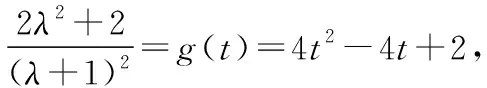
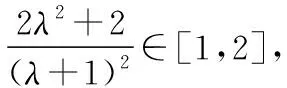
【点评】本题考查向量的坐标运算、向量的数量积、两向量的夹角、基本不等式以及二次函数等.
三、扩大成果绵绵悠长
第一阶段的试题“原创研发”虽然告一段落了,但活动留给我们的精神似清风和雨、绵绵悠长.试卷可谓题题经典、漂亮,内涵丰富,莫让原创试题“尘封”,进一步充分挖掘原创试题所潜在的教育功能、应用功能和拓展功能,扩大“原创研发”的成果,是此次原创研发活动的主旨,也是我们接下来需要而且是很有必要做的有意义的事情.下面通过“扩大”两道原创、研发题(文、理各一道)的“成果”,藉以抛砖引玉.
( )

C.4 D.2
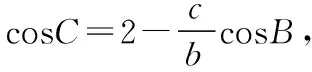
示例11.(原创卷文13)在△ABC中,角A,B,C所对的边分别为a,b,c,有A,C,B成等差数列,且acosB+bcosA=2,则△ABC面积的最大值为________.
【解析】由A,C,B成等差数列,得2C=A+B,

由射影定理可得c=2.
所以由余弦定理c2=a2+b2-2abcosC
得a2+b2-ab=4,由a2+b2≥2ab

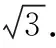
1.规律分析
这两道试题不谋而合,运用三角形中的“射影定理”解答方便简捷.无独有偶,在2017高考中,全国Ⅱ卷文和山东卷对“射影定理”的应用都作了考查.“射影定理”虽然是一个较小的知识点,但最近几年高考几乎每年都考查到,且常看常新.不以“点小”而“不为”,重视“射影定理”,应用它解题,尤其是解答客观题会收到意想不到的效果.两道原创研发题和高考题都起到了很好的导向作用.
射影定理:设△ABC的内角A,B,C对应的边分别是a,b,c,则a=bcosC+ccosB,b=acosC+ccosA,c=acosB+bcosA.
【证明】已知余弦定理:a2=b2+c2-2bccosA,①
b2=c2+a2-2cacosB,②
c2=a2+b2-2abcosC.③
①②两式相加,得2c2-2bccosA-2cacosB=0,
即c=acosB+bcosA.
同理可证a=bcosC+ccosB,b=acosC+ccosA.
2.变式应用
示例10是求值问题,示例11是求最值问题,结合历年高考题再进一步说明“射影定理”在其他方面的应用.
2.1.求角
变式1.(2017·全国卷Ⅱ·文16)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=________.
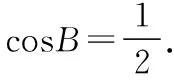
2.2.判断三角形的形状
变式2.(2013·陕西卷·理7)设△ABC的内角A,B,C对应的边分别是a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为
( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
【解析】由射影定理a=bcosC+ccosB,得a=asinA,所以sinA=1,即A=90°,所以△ABC是直角三角形.故选B.
2.3.结论判断
变式3.(2017·山东卷·理9)在△ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是
( )
A.a=2bB.b=2a
C.A=2BD.B=2A
【解析】因为sinB(1+2cosC)=2sinAcosC+cosAsinC,
所以由正弦定理得b(1+2cosC)=2acosC+ccosA,
即b+2bcosC=acosC+(acosC+ccosA).
所以由射影定理b=acosC+ccosA,
得b+2bcosC=acosC+b.
因为cosC≠0,所以a=2b.故选A.
总之,原创卷具有较高的信度、效度和有效的区分度,达到了“考基础、考能力、考素质、考潜能”的考试目标,对我们备战2018年高考有很好的启迪和指导意义.

