转化是解题的“利器”

江苏 陆道春 郭建华

解决数学问题就是从未知向已知转化的过程.化归与转化的思想是解决数学问题的根本思想，解题的过程实际上就是一步步转化的过程.学数学离不开解题.通过解题，学生可以加深概念的理解，深化对概念联系性的认识，优化数学认知结构，提高分析问题和解决问题的能力.要想快速解题，就要增强转化意识.“转化”是所有数学思想方法中最基本、最核心的一种思想方法，事实上，许多数学思想都体现了转化的本质.对于较难习题，首先要深刻理解题意，再给予合理的等价转化，将陌生问题转化为熟悉问题，它是一种培养知识迁移能力的重要学习方法．在解题过程中，引导学生抓住题目中已知关键信息以及隐藏信息，锁定目标，由易到难，由浅入深，逐步探究．因此，教师在习题教学实践中，依据习题的特征，结合具体教学内容以及学生的认知水平，充分调动学生学习数学的积极性和主动性，增强转化意识，不断优化学生的思维品质，从而提高解题能力.

一、巧用公式 化繁为简

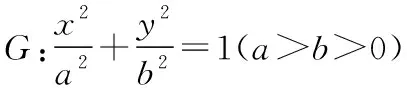
(1)求椭圆G的方程；

(2)求四边形ABCD面积的最大值.

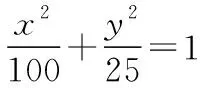
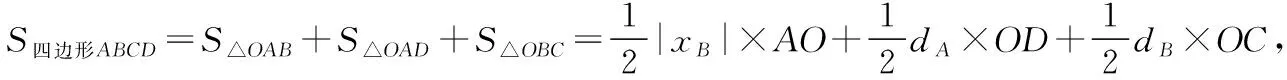
【评析】学生的运算能力弱已经成了普遍现象.在解题教学过程中，精心设计和选择典型示例是关键，引导学生在解题过程中不仅仅关注解题的思路和方法，更应该加强指导学生在运算过程中的合理性、简洁性等深化对定理、公式、法则在本质上的理解和对典型习题的总结和提炼才能增强转化的意识．比如本题就是一道非常典型的分式函数求最值问题，并没有按部就班的做，而是通过观察式子的结构，巧妙地使用重要不等式，使得解题简洁迅速.因此，只有善于思考学生的运算问题，才能有效地提升学生的运算能力．

二、反客为主 出奇制胜

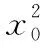
【评析】对于求解一类含参方程f(a,x)=0(a为参数)的自变量x被限定在某个范围的有解问题，如果从正面求解实数a的范围，要面临很繁琐的讨论，因此就把a当做主元，即a=g(x)，转换为求a=g(x)关于自变量x的值域问题.当利用主元难以求解时，考虑从次元出发(化客为主)，并把主元放在次元的位置上进行处理，实施战略转移，可能让我们看到原来看不到的结构，容易发现解决问题的关键，找到处理问题的方法，它是一种换位法，体现了向对立面转化的特点.

三、转换视角 别具匠心

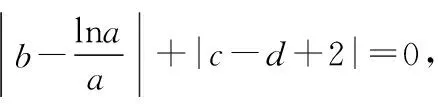
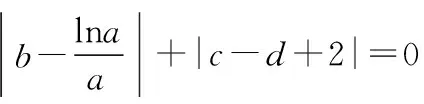
【评析】有些多元最值问题表面上看起来比较繁琐，甚至感到无从下手，若换个角度思考，通过观察题设条件的结构，挖掘题设条件中所隐含的几何本质，便可找到解题的切入点.比如本题解题的关键是将代数问题几何化，由代数式的结构特征联想到其表示的几何意义，其难点在于如何将题设条件抽象出点的轨迹方程，并将动点间的距离问题借助导数来分析，对培养学生的抽象思维素养有一定的帮助.

四、构造方程 柳暗花明

【例4】在平面直角坐标系xOy中，已知圆O1，圆O2均与x轴相切且圆心O1，O2与原点O共线，O1，O2两点的横坐标之积为6，设圆O1与圆O2相交于P，Q两点，直线l：2x-y-8=0，则点P与直线l上任意一点M之间的距离的最小值为________．

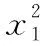
【评析】根据已知条件与所求式子的特征，探寻问题的结构特征和数量关系，挖掘潜在已知与未知因素，从而联想有关的方程(或方程组)，利用方程理论求解，使问题在新的关系下转化，将陌生问题熟悉化，复杂问题简单化.

五、化动为静 出奇制胜

【例5】已知圆C:(x-2)2+(y-1)2=5，与y轴正半轴的交点为B，设点P，Q分别是直线l:x+y+2=0与圆C上的动点，求|PB|+|PQ|最小值及此时点P的坐标．

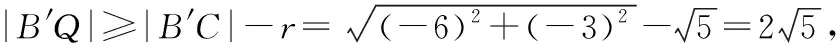
【评析】化动为静是处理动态问题的有效方法，“定”指的是“定态”，例如临界态等；也可以是大家头脑中已经定型的认识——“定式”，例如某些规律、定理等；也可以是变化的因和果——“定点”.从这些“定态”、“定式”、“定点”入手分析动态问题，往往能顺利找到其动态变化规律，从而达到以不变应万变的效果，比如本题利用对称性把问题转化为求圆外一点到该圆上一点的最小值问题，进而转化为两定点B′和C的距离问题.

六、正难则反 另辟蹊径

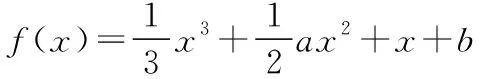
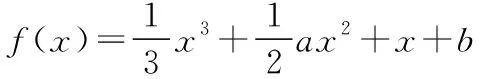
【评析】一个命题的题设和结论是因果关系的辩证统一.对某些题目从正面解比较复杂，比较抽象，并且条件和结论之间的关系不明确；或者从正面入手思维受阻；或者从正面解决，需要进行多方面的讨论，很繁琐，不妨从它的反面出发，逆向思维，往往会起到事半功倍的效果.