关注数学解题中的思维“灵动”

陕西 李 歆

在数学解题时，按照已经熟悉的套路或者一定的模式去处理，固然很重要，但有时这样做比较费时、费力，甚至陷入困境，如果能打破常规，因题而动，学会捕捉有效的隐含信息，让思维“灵动”起来，那么往往能达到迅速快捷、出奇制胜的解题效果.

1.对某些线性规划问题，利用不等式的基本性质，对约束条件中的同向不等式相加，可简化解题

( )

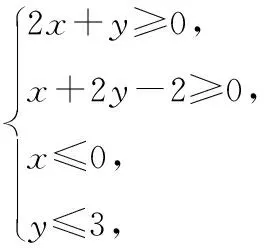
【分析】求解此类问题，通常都要先利用线性约束条件作出可行域，然后根据几何意义找到目标函数的最优解，但注意观察约束条件，上面是两个“≥”同向不等式，下面是两个“≤”同向不等式，由此出发，即可利用不等式的基本性质迅速求解.

【解】将不等式x≤0与y≤3，两边分别相加，得x+y≤3，当且仅当x=0，y=3时等号成立(此时约束条件中前两个不等式也成立).故目标函数z=x+y的最大值为3，故选D.

( )

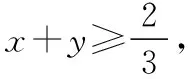
A.2 B.3

C.4 D.5

【分析】约束条件中最上面是两个“≤”同向不等式，相加后即可得到目标函数不等式.

【解】将不等式2x-y≤0，x+2y-5≤0，两边分别相加，得3x+y≤5，等号当且仅当x=1,y=2时成立(此时约束条件中第三个不等式也成立).所以3x+y的最大值为5,故选D.

【点评】如果要求3x+y的最小值，必须出现两个“≥”同向不等式，而约束条件中已经有了一个不等式x≥0，另一个可通过对不等式2x-y≤0变号，得-2x+y≥0，给前面的不等式两边乘以5后，再与后面的不等式两边分别相加，得3x+y≥0,当且仅当x=0,y=0时等号成立(此时约束条件中第二个不等式也成立).所以3x+y的最小值为0.

2.对某些二项式问题，利用多项式乘法或者特殊值法，可思路顺畅

【例2】(2017·浙江卷)已知多项式(x+1)3(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,则a4=______ ,a5=

.

【分析1】看到此题，一般会想到二项式定理，但因出现了两个二项式相乘的问题，给解题带来了麻烦，考虑到两个二项式的次数分别为3,2，不妨试一试多项式乘法.

【解法1】由于(x+1)3(x+2)2

=(x3+3x2+3x+1)(x2+4x+4)

=x5+(4x4+3x4)+(4x3+12x3+3x3)+(12x2+12x2+x2)+(12x+4x)+4

=x5+7x4+19x3+25x2+16x+4,

所以a4=16,a5=4.

【分析2】观察多项式的展开式，要求的两项分别是一次项的系数和常数项，易知常数项就是两个二项式的常数项相乘，而一次项的系数则是每个二项式的一次项系数与另一个二项式的常数项相乘的和.

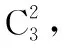
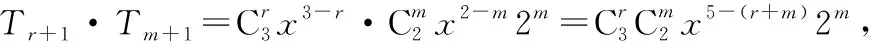
【变式】已知多项式(x+1)4(x+2)3=x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7,则a1+a3+a5=______ ,a2+a4+a6=______ .

【分析】很显然，要求出a1，a2，a3，a4，a5,a6相当麻烦，比较多项式两边的结构特点，可以用赋值法求解.

【解】在多项式中，取x=0,得a7=8;

取x=1，得a1+a2+a3+a4+a5+a6=423 ①;

取x=-1，得a1-a2+a3-a4+a5-a6=-7 ②,

①加②，得a1+a3+a5=208，

①减②，得a2+a4+a6=215.

【点评】赋值法是一种常用的解题方法，若用得及时，用得巧妙，则具有“一两拨千金”之效.

3.对某些含参数的绝对值函数的最值，转化为不等式恒成立问题，可化难为易

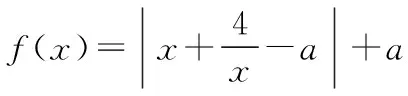
【分析】这是含有绝对值的函数最值问题，通常都要把函数f(x)先化为分段函数，然后求解，但因此题中带有参数，又增加了题目的难度.如果利用绝对值不等式的性质：|f(x)|≤a⟺-a≤f(x)≤a，那么就可以化难为易.

【点评】此解巧妙地利用等价转化思想和不等式恒成立时的条件，使问题迎刃而解，这说明灵活地运用课本上的基础知识和已经熟悉的解题方法，可以达到出奇制胜的解题效果.

【解】参考上述例3的解析过程,易得所求a的取值范围为(-∞,0].

4.对某些数列不等式的证明，将“通项公式”放缩转化为“通项”放缩，可转危为安

【例4】(2014·全国卷Ⅱ理)已知数列{an}满足a1=1，an+1=3an+1.

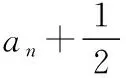
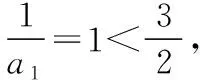
综上可知,所证不等式成立.

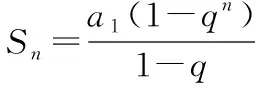
【变式】已知数列{an}满足a1=1，an+1=3an+2.

(Ⅰ)求{an}的通项公式；

【分析】第(Ⅰ)问比较简单，由an+1+1=3(an+1)，可得数列{an+1}是首项为2，公比为3的等比数列，所以an=2×3n-1-1.

【证明】由an+1=3an+2，得an+1>3an，

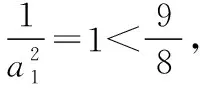
当n≥2时,由③式，

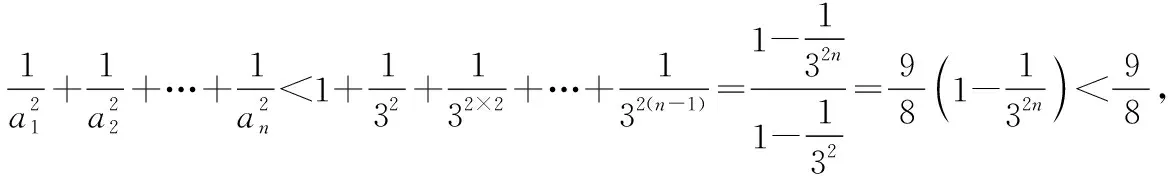
综上可知,所证不等式成立.

【点评】观察②式和③式，竟然是同一个不等式，虽然它们获得的放缩过程不同，但是都绕过了对“通项公式”的放缩，将放缩的目标都聚焦到“an”上，突破点是完全相同的.所以，同学们要养成“题不变我不变”“题若变我必变”的解题战略思想，不断提升用不同的方法去解同一道数学题的能力.

“数学是锻炼思维的体操”.数学解题中的思维，根在课本，源自基础，思维“灵动”并非胡思乱想、奇思妙想、突发奇想，而是针对不同的问题和条件，让思维灵活运转，既排除困难，又绕过麻烦，合理选择最佳的解题策略.做数学人，解数学题，非一日之功.常言道，熟能生巧，希望同学们熟通法之大道，生灵动之精巧，悟解题之真谛.