数学解题中常见的策略性失误

安徽 唐录义

策略性失误是指解题方向上的偏差或方法策略上的笨拙，造成思路受阻，或导致解题难度增大，致使出错的概率增大或潜在失分.

一、未切中问题本质

要解决一个数学问题,关键在于能否把这个数学问题“看破”，即把握解决问题的核心与关键,揭示问题的本质.在解题过程中,如何有效地揭示一个问题的本质，让学生真正了解知识的来龙去脉,回到问题起点，则需要从问题所涉及的基本概念、性质与思想方法出发,分析思考问题,并由此来把握解决问题的关键,揭示问题的本质,以达到较快解决问题的效果.

案例1(2015·四川卷理·19)如图，A，B，C，D为平面四边形ABCD的四个内角.

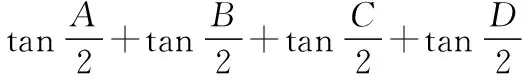
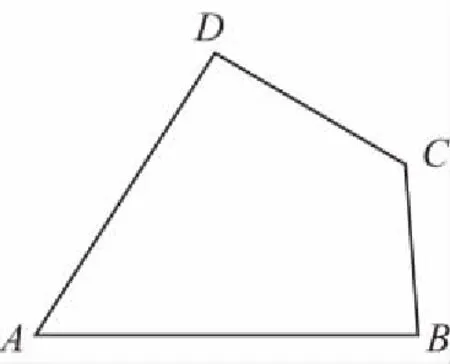
【考点涉及】二倍角公式，诱导公式，余弦定理，简单的三角恒等变换．

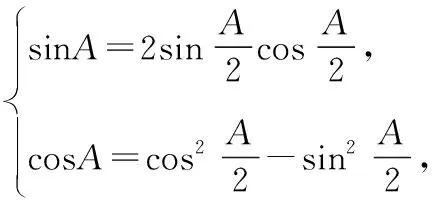
化简后则进行不下去.

【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)(1)数学的某些题的解题思路来得简单，但不一定能够运算下去，不具有可行性.(2)不能根据所给边长和角A角C的互补关系，构造三角形，由余弦定理建立等式求出A角B角的正弦值.

【出错归因】由待证结构式发现，需要用倍角的正余弦表示半角的正切，很容易想到升幂公式，但停留在联立这一步，使得运算量很大，无法进行下去；不能将四边形转化成三角形处理，这是心理性失误,理解不透，忽略隐含条件，不能利用角A角C的互补关系建立等式，这是策略性失误,未着眼问题本质，陷入求解困境.

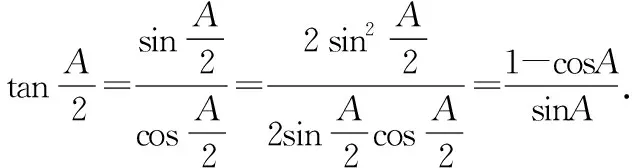
连接BD，在△ABD中，

有BD2=AB2+AD2-2AB·ADcosA，

在△BCD中，

有BD2=BC2+CD2-2BC·CDcosC，

因为A+C=180°,

所以AB2+AD2-2AB·ADcosA=BC2+CD2+2BC·CDcosA，

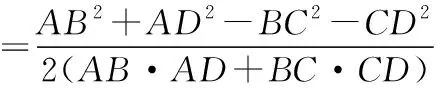
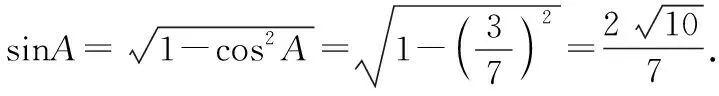
连接AC，同理可得

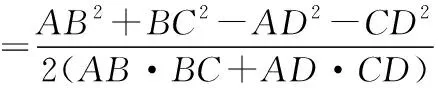
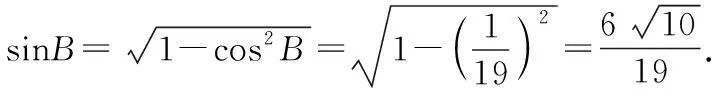
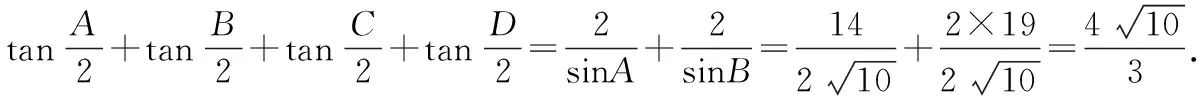
【反思总结】本题的错解,展示了数学解题的一种现象：思路来得很常规，理论分析也没问题，但不一定有运算结果.因此，数学思考必须要严谨，注重可行性，想到了升幂公式，若再进一步思考升幂降幂公式特征，不难想到倍角表示单角必须在幂上是单角的二次幂，所以要升幂，再化简，问题就迎刃而解.高考中经常将三角恒等变换与解三角形知识综合起来命题，本题第(Ⅰ)题的证明为第(Ⅱ)题的化简提供了保证.恒等式证明与代数式证明一样，主要证明方法有从左到右或从右到左；左右归一或变更命题.选择哪一种证法的依据是“化繁为简”.观察函数名和角，想到切化弦和升幂公式，得证.第(Ⅱ)题利用转化与化归思想将四边形变成三角形，根据正余弦定理启用两角互补关系和一组公共边，建立两个方程，解决两个未知数.本题很好的考查运算求解能力、推理论证能力.

二、解题角度不当

找到一个恰当的解题角度，知识就会为你打开一扇通向解题成功的大门，反之，解题角度不当，就会增大难度，甚至根本就找不到解题的方法.

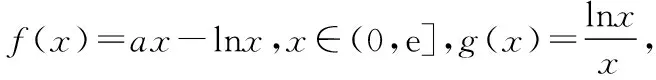
(Ⅰ)讨论a=1时，函数f(x)的单调性和极值；

【考点涉及】函数单调性的判断，不等式，极值的判断.

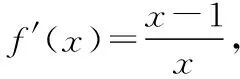
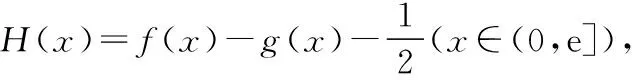
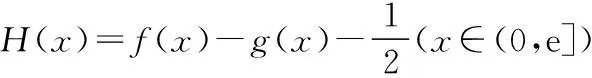
【出错归因】策略性失误：解题角度不当，增大求解难度.

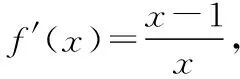
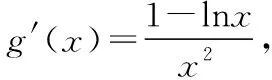
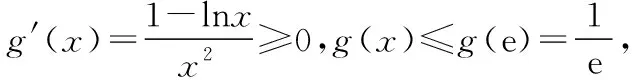
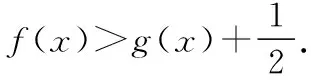
【反思总结】构造函数是解导数问题的基本方法，也是高考中的热点问题，如何合理的构造函数，不仅是教学的难点，也是学生学习的难点和困惑.构造合理，就会使证明过程简洁而又准确.但数学问题是千变万化，解题方法也是多种多样，善于构造，但不能局限于构造，才是我们解决导数这类问题的根本之道.

三、解题方法不当

一个数学问题的求解可采用的策略可能有多种,但好的策略不仅可以使问题的求解过程简洁明快,而且决定着问题的最终正确解决．差的方法策略会产生曲折的思维回路,舍简求繁，方向不准，误入歧途，从而使问题求解受阻,或增大求解的难度与长度,即使解出来了也因费时费力而产生潜在失分.

案例3已知{an}是递增数列，且对任意n∈N*都有an=n2+λn恒成立，则实数λ的取值范围是

( )

A.[0，+∞) B.(1，+∞)

C.[-2，+∞) D.(-3，+∞)

【考点涉及】数列的单调性，恒成立问题.

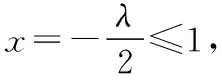
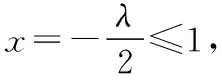
【出错归因】方向不准，判断数列单调性的方法不当.

【正解参考】因为{an}是递增数列，所以an0对任意n∈N*恒成立，可得λ>-2n-1对任意n∈N*恒成立，又-2n-1≤-3所以λ>-3.故正确答案选D.

【反思总结】数列作为一种特殊的函数，是反映自然规律的基本数学模型.如果数列{xn}满足xnxn+1，n=1,2,3，…，则称数列{xn}为单调递减数列.主要判定方法有：比较法、函数法、导数法等.

四、模型选择不当

数学模型是一种模拟，是用数学符号、数学式子、程序、图形等对实际问题本质属性的抽象而又简洁的刻画，它或能解释某些客观现象，或能预测未来的发展规律，或能为控制某一现象的发展提供某种意义下的最优策略或较好策略.数学模型一般并非现实问题的直接翻版，它的建立常常既需要人们对现实问题进行深入细微的观察和分析，又需要人们灵活巧妙地利用各种数学知识.这种应用知识从实际问题中抽象、提炼出数学模型的过程就称为数学建模．如果模型选择不当，得出的结果可能与实际相差甚远，使预测失真，会导致决策失误．

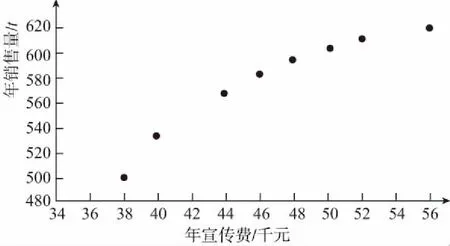
案例4(2015·全国卷Ⅰ·文19理19)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：千元)对年销售量y(单位：t)和年利润z(单位：千元)的影响，对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理，得到下面的散点图及一些统计量的值.

x y w∑8i=1(xi- x)2∑8i=1(wi- w)246.65636.8289.81.6∑8i=1(xi-x)(yi-y)∑8i=1(wi-w)(yi-y)1 469108.8

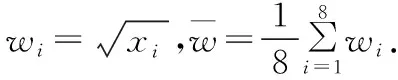
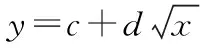
(Ⅱ)根据(Ⅰ)的判断结果及表中数据，建立y关于x的回归方程.

(Ⅲ)已知这种产品的年利润z与x，y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:

(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?

(ⅱ)年宣传费x为何值时,年利润的预报值最大?

附:对于一组数据(u1，v1)，(u2，v2)，…，(un，vn)，其回归直线v=α+βu的斜率和截距的最小二乘估计分别为

【考点涉及】散点图，线性回归，非线性回归，回归分析.

【错解呈现】(Ⅰ)由散点图可以判断，y=a+bx适宜作为年销售量y关于年宣传费x的回归方程类型.

(Ⅱ)建立y关于w的线性回归方程.由于

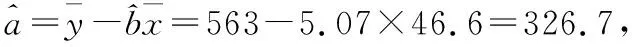
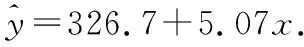
【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)显然，由散点图可知y关于x的函数图象更可能是抛物线，y=a+bx不适宜作为年销售量y关于年宣传费x的回归方程类型.

【出错归因】模型选择不当，观察能力不足.

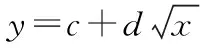
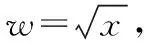
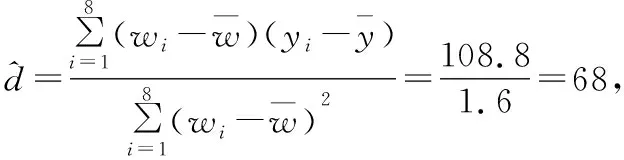
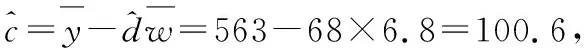
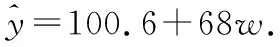
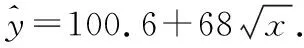
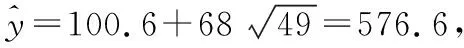
(ⅱ)根据(Ⅱ)的结果知，年利润z的预报值

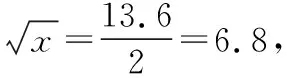
故年宣传费为46.24千元时，年利润的预报值最大.

【反思总结】本题考查了化归与转化的思想，将非线性回归问题转化为线性回归问题,题目给出线性回归方程系数公式以及有关数据.根据回归方程进行预测预报，并利用二次函数求最值，体现了函数思想的运用.