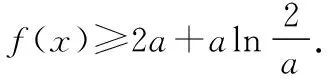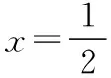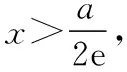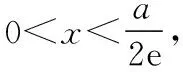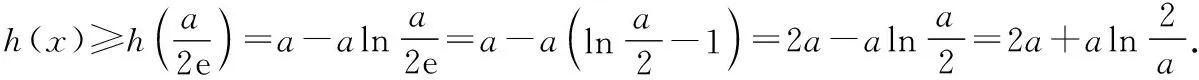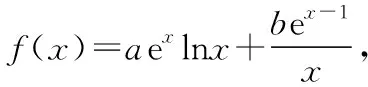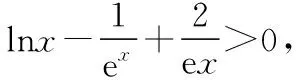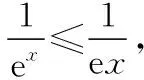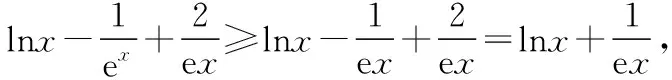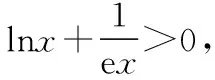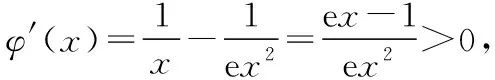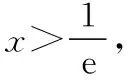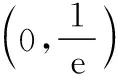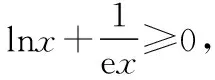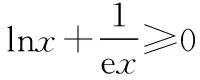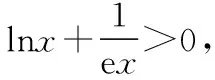两个指对函数不等式的作用被低估了
——读《教学考试》有感
陕西 蔡正文 彭 健
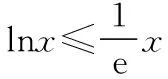
一、关于不等式ex≥ex的证明与应用
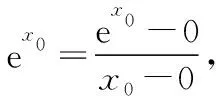
【例】(山阳中学2017届11月月考题)已知函数f(x)=ax2-ex(x∈R).
(Ⅰ)当a=1时,试判断f(x)的单调性并给予证明;
(Ⅱ)若f(x)有两个极值点x1,x2(x1 (ⅰ)求实数a的取值范围; 解:(Ⅰ)当a=1时,f(x)=x2-ex在R上单调递减,证明如下. 因为f′(x)=2ax-ex,当a=1时,f′(x)=2x-ex, 又曲线y=ex过原点的切线是y=ex, 所以当x≤0时,f′(x)=2x-ex<0, 当x>0时,ex>2x,故f′(x)=2x-ex<0, 所以当x∈R时,f′(x)=2x-ex<0, 当a=1时,f(x)=x2-ex,f(x)在R上单调递减. 由(ⅰ)易知x1∈(0,1), 即f(x1)在(0,1)上单调递减,故f(1) 评注:①巧妙利用不等式ex≥ex,可回避分类讨论和二次求导; ②利用这种方法比其他方法更便于发现极值点x1在区间(0,1)上,有利于(ⅱ)的证明; ③对于导函数是f′(x)=bex-ax形式的都可以用此方法来判断f′(x)的正负. 【例】已知函数f(x)=ax2+x(1-lnx)(a∈R). (Ⅱ)若f(x)有两个极值点. (ⅰ)求实数a的取值范围; 解:因为f(x)的定义域为(0,+∞), (ⅱ)若f(x)有两个极值点x1,x2,其中x1 由(ⅰ)知当x∈(0,x1)时,f′(x)>0; 当x∈(x1,x2)时,f′(x)<0; 当x∈(x2,+∞)时,f′(x)>0; 由(ⅰ)知x1∈(1,e), ②利用这种方法比其他方法更便于发现极值点x1在区间(1,e)上,有利于(ⅱ)的证明; ③对于导函数是f′(x)=blnx-ax形式的都可以用此方法来判断f′(x)的正负. 这两个不等式在解答某些高考题中也有一定的应用,下面结合近年课标卷高考题加以说明,仅供参考. 【例1】(2015·全国卷Ⅰ文·21)设函数f(x)=e2x-alnx. (Ⅰ)讨论f(x)的导函数f′(x)零点的个数; 解:(Ⅰ)略. 评注:①此解法避免了出现导函数零点不可求的局面; ②也避免了设导函数零点后,代入原函数的较高技巧性; (Ⅰ)求a,b; (Ⅱ)证明:f(x)>1. 解:(Ⅰ)略. 因为不等式ex≥ex中取“=”的条件是x=1, 评注:①通过不等式ex≥ex>0放缩得到新函数φ(x),它的导函数零点可求; ②从而问题就转化为证明新函数φ(x)的最小值大于零的问题; ③这种处理方法大大降低了原题第(Ⅱ)问的思维难度.
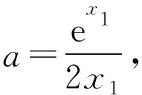

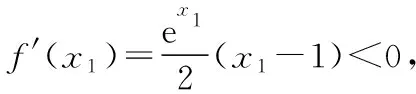
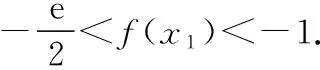
二、关于不等式的证明与应用
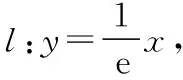
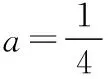
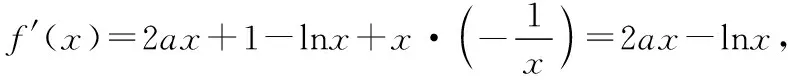
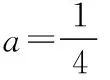
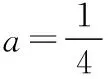
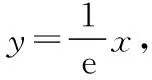
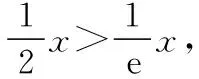
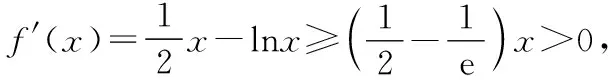
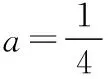
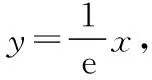
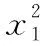
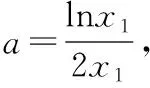
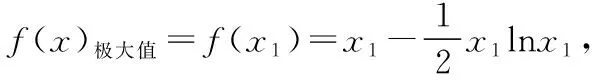
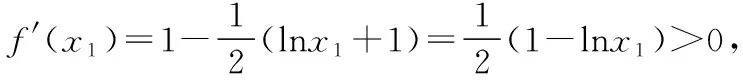
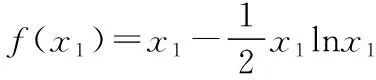
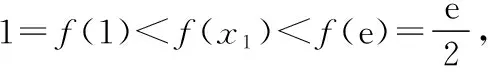

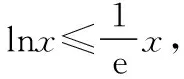
三、应用举例