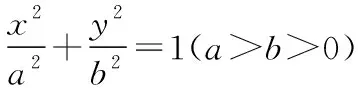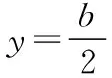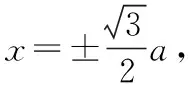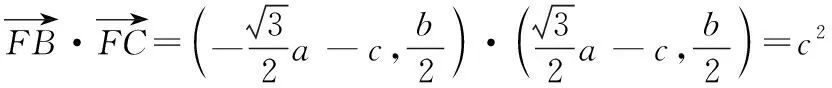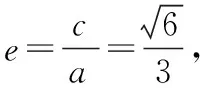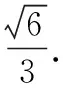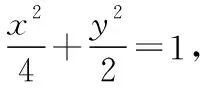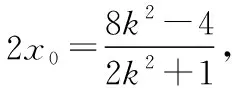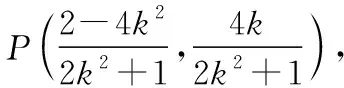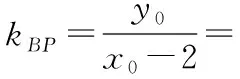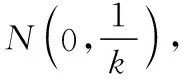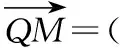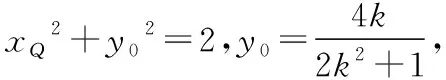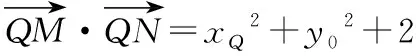优化运算巧解题,圆锥曲线妙突破
江苏 韩文美
简化解题过程是我们追求的目标,由于圆锥曲线问题运算量大、综合性较强,很多问题可能会因为冗长的运算、繁琐的推理而导致无法进行到底,从而半途而废,望题兴叹.因此,在解答圆锥曲线问题时必须研究技巧与策略,寻求突破点,选用适当方法,以求做到选择捷径、简化计算、避繁就简、合理解题,收到事半功倍之效.
1.回归定义,以逸待劳
回归定义的实质是重新审视概念,并用相应的概念解决问题,是一种朴素而又重要的策略和思想方法.圆锥曲线的定义既是有关圆锥曲线问题的出发点,又是新知识、新思维的生长点.对于相关的圆锥曲线中的数学问题,若能根据已知条件,巧妙灵活应用定义,往往能达到化难为易、化繁为简、事半功倍的效果.
【典例1】(2016·全国卷Ⅰ理·20(Ⅰ))设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.证明|EA|+|EB|为定值,并写出点E的轨迹方程.
【分析】通过平行线的性质,结合圆的相关性质,通过三角形中等角对等边的转化确定定值问题,并利用椭圆的定义来求解相应的轨迹方程.
【解析】如图,因为|AD|=|AC|,EB∥AC,
故∠EBD=∠ACD=∠ADC,所以|EB|=|ED|,
故|EA|+|EB|=|EA|+|ED|=|AD|,
又圆A的标准方程为(x+1)2+y2=16,
从而|AD|=4,所以|EA|+|EB|=4,
由题设得A(-1,0),B(1,0),|AB|=2,
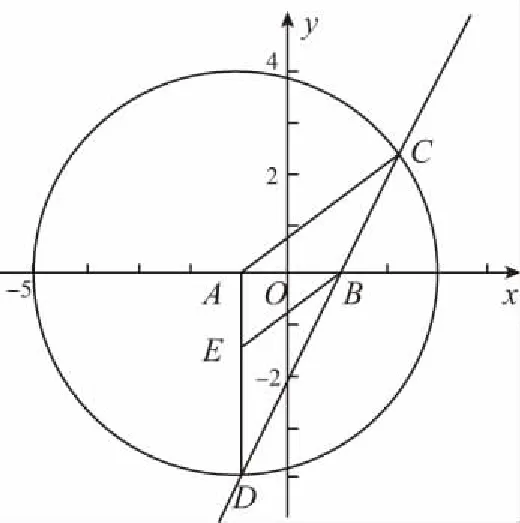
【点评】本题主要考查平行线的性质,圆的相关性质与三角形的性质,椭圆的定义与轨迹方程的求解.圆锥曲线的定义揭示的是事物的本质属性,对于相关的圆锥曲线中的数学问题,若能巧妙灵活应用定义,往往能达到化繁为简、事半功倍的效果.
【变式1】(2015·浙江卷理·5)如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是
( )
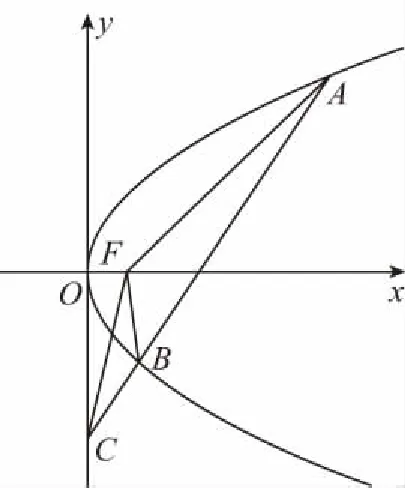

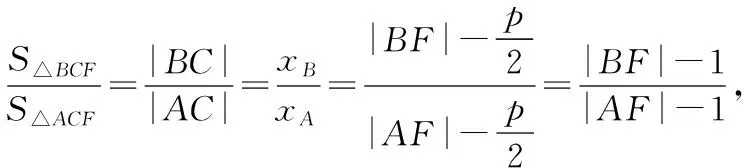
2.巧设参数,变换主元
巧设参数的实质是通过引入参变量加以替换,使得圆锥曲线中相关或不相关的量统一在参变量下,减少未知量的个数,这样解决问题更方便,同时可以进一步体会解决问题中数学方法的灵活多变.
【典例2】(2015·四川卷文、理·10)设直线l与抛物线y2=4x相交于A,B两点,与圆C:(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB中点,若这样的直线l恰有4条,则r的取值范围是
( )
A.(1,3) B.(1,4)
C.(2,3) D.(2,4)
【分析】先设出直线l的方程x=ty+m(这样可以避免讨论直线的斜率是否存在问题),根据直线与抛物线相交于两点得到Δ=16t2+16m>0,结合根与系数的关系与中点坐标公式确定点M的坐标,利用直线l与圆相切,分别得到两直线垂直以及半径的关系式,进而得以判断r的取值范围.
【解析】不妨设直线l的方程为x=ty+m,
A(x1,y1),B(x2,y2),
代入抛物线y2=4x并整理得y2-4ty-4m=0,
则有Δ=16t2+16m>0,y1+y2=4t,y1y2=-4m,
那么x1+x2=(ty1+m)+(ty2+m)=4t2+2m,
可得线段AB的中点M(2t2+m,2t),
而由题可得直线AB与直线MC垂直,
即kMC·kAB=-1,
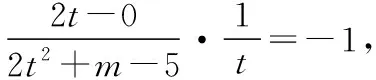
整理得m=3-2t2(当t≠0时),
把m=3-2t2代入Δ=16t2+16m>0,
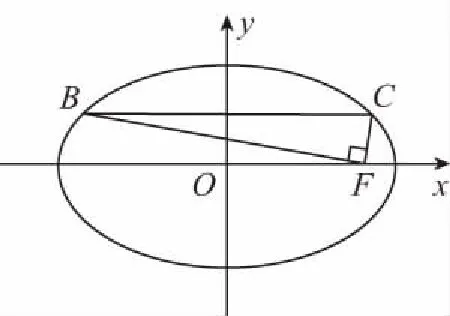
可得3-t2>0,即0 又由于圆心到直线的距离等于半径, 而由0 【点评】本题主要考查直线与抛物线的位置关系,直线的方程与应用,点到直线的距离公式,考查运算求解能力、函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想等.巧妙通过直线方程的设置,引入参数,利用直线与圆锥曲线的位置关系加以转化,结合题目条件通过分析参数的取值范围达到解决问题的目的. 【解析】设P(x0,y0)(x0<0,y0<0),则x02+4y02=4, 又A(2,0),B(0,1), 所以四边形ABNM的面积 =2, 从而四边形ABNM的面积为定值. 设而不求是解析几何解题的基本手段,是比较特殊的一种思想方法,其实质是整体结构意义上的变式和整体思想的应用.设而不求的灵魂是通过科学的手段使运算量最大限度地减少,通过设出相应的参数,利用题设条件加以巧妙转化,以参数为过渡,设而不求. ( ) 【分析】设出相应的直线l的方程,结合题目条件确定 |FM| 与|OE|的长度,利用△OBG∽△FBM的性质加以转化,进而利用椭圆的离心率公式加以分析,采用“设而不求”思想. 【解析】设OE的中点为G,由题意设直线l的方程为 y=k(x+a), 分别令x=-c与x=0得|FM|=k(a-c),|OE|=ka, 故选择答案:A. 【点评】本题主要考查直线与椭圆的位置关系,三角形相似的性质与应用,椭圆的几何性质等.在运用圆锥曲线问题中的设而不求方法技巧时,需要做到:(1)凡是不必直接计算就能更简洁地解决问题的,都尽可能实施“设而不求”;(2)“设而不求”不可避免地要设参、消参,而设参的原则是宜少不宜多. 【解析】设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM), (2k2+1)x2+4kbx+2b2-8=0, 所以直线OM的斜率与直线l的斜率的乘积为定值. 著名数学家华罗庚说过:“数与形本是两相倚,焉能分作两边飞.数缺形时少直观,形少数时难入微.”在圆锥曲线的一些问题中,许多对应的长度、数式等都具有一定的几何意义,挖掘题目中隐含的几何意义,采用数形结合的思想方法,可解决一些相应问题. 【分析】要求△APF的周长的最小值,其实就是转化为求解三角形三边长之和,根据已知条件与双曲线定义加以转化为已知边的长度问题与已知量的等价条件来分析,根据直线与双曲线的位置关系,通过数形结合确定点P的位置,通过求解点P的坐标进而利用三角形的面积公式来处理. 【解析】设双曲线的左焦点为F1,根据双曲线的定义可知|PF|=2a+|PF1|, 则△APF的周长为|PA|+|PF|+|AF|=|PA|+2a+|PF1|+|AF|=|PA|+|PF1|+|AF|+2a, 由于|AF|+2a是定值,要使△APF的周长最小, 则|PA|+|PF1|最小,即P,A,F1共线, 【点评】本题主要考查双曲线的定义、标准方程与几何性质,直线方程,直线与双曲线的位置关系等.数形结合的思想是数学重要的思想方法之一,其具有直观性、灵活性、深刻性,并有跨越各知识点的界线,有较强的综合性.数形结合的思想的实质就是把抽象的数学语言与直观的图形结合起来,把抽象思维与形象思维结合起来.利用数形结合来求解参数问题,解答更形象、直观,一目了然. 【变式4】已知抛物线C:y2=8x,点P为抛物线上任意一点,过点P向圆D:x2+y2-4x+3=0作切线,切点分别为A,B,则四边形PADB的面积的最小值为 ( ) 【解析】如图所示,圆D:(x-2)2+y2=1,该圆的圆心与抛物线焦点重合,半径为1, 则S四边形PADB=2SRt△PAD=|PA|, 当四边形PADB的面积最小时,|PD|最小, 过点P向抛物线的准线x=-2作垂线,垂足为E, 则|PD|=|PE|,当点P与坐标原点重合时, |PE|最小,此时|PD|=|PE|=2, 故选择答案:A. 极端策略是一种重要的数学思想,灵活地借助极限思想,从有限到无限,从近似到精确,从量变到质变.通过圆锥曲线问题的极端元素,灵活借助极端策略解题,可以避开抽象及复杂运算,优化解题过程,降低难度,是简化圆锥曲线运算的一条有效且重要途径. 【分析】根据双曲线的定义得到关系式|PF1|=|PF2|+2,通过分类讨论,结合极限思想确定当∠F1PF2=90°时与当∠F1F2P=90°时关系式的最值,数形结合即可得△F1PF2为锐角三角形时关系式的取值范围. 假定P是双曲线上第一象限内的点, 由双曲线的定义知|PF1|―|PF2|=2a=2, 则有|PF1|=|PF2|+2, 当∠F1PF2=90°时, 有|PF1|2+|PF2|2=|F1F2|2, 可得|PF2|2+2|PF2|―6=0, 当∠F1F2P=90°时,有|PF1|2=|PF2|2+|F1F2|2, 可得|PF2|=3,此时|PF1|+|PF2|=8; 而△F1PF2为锐角三角形, 【点评】本题主要考查双曲线的定义、标准方程与几何性质,焦点三角形问题.应用极端策略来解决一些问题时,可以避开抽象、复杂的运算,独辟蹊径,降低解题难度,优化解题过程,起到事半功倍的效果. 【解析】由已知可求得P(2,3),Q(2,-3),故|PQ|=6, 消去y并整理可得x2+tx+t2-12=0, 故x1+x2=-t,x1x2=t2-12, 且Δ=t2-4(t2-12)>0,解得-4 所以四边形APBQ的面积 从对称性角度不难猜测, 当t=0时,四边形APBQ的面积最大, 平面向量是衔接代数与几何的纽带,沟通“数”与“形”,融数、形于一体,是数形结合的典范,具有几何形式与代数形式的双重身份,是数学知识的一个交汇点和联系多项知识的媒介.妙借向量,可以有效提升圆锥曲线的解题方向与运算效率,达到良好效果. 【分析】根据题目条件确定B,C的坐标,通过相关向量的坐标的确定,结合∠BFC=90°,利用相应的向量的数量积来转化,进而结合椭圆的离心率公式达到求解的目的. 而F(c,0), 【点评】本题主要考查椭圆的标准方程与几何性质,平面向量的坐标运算与数量积等.巧妙借助平面向量的坐标运算来转化圆锥曲线中的相关问题,从形入手转化为相应数的形式,简化运算,进而达到解决圆锥曲线的几何性质的目的. 【解析】∠MQN是定值90°,证明如下: 设P(x0,y0),直线AP:y=k(x+2)(k≠0), 令x=0可得M(0,2k), 整理可得(2k2+1)x2+8k2x+8k2―4=0, 所以QM⊥QN,故∠MQN是定值90°. 我们可以从灵活运用圆锥曲线定义、性质的角度出发,利用相应的媒介,选择恰当的思维策略,以求简洁明快地解决对应的圆锥曲线问题.这样,对于圆锥曲线问题中的简化运算,培养处理圆锥曲线问题科学的思维方式,提升解题能力等具有重要作用.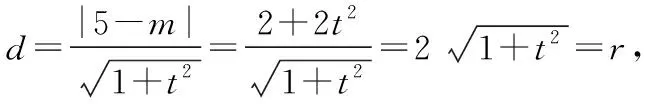
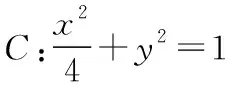

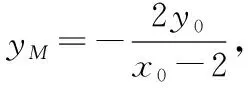
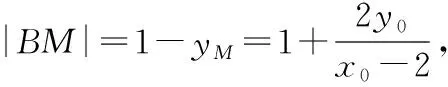
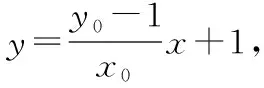

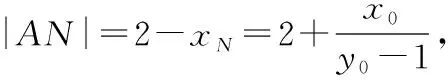
3.设而不求,金蝉脱壳

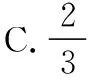

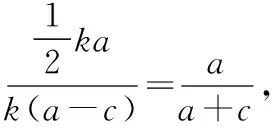
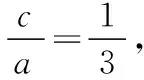
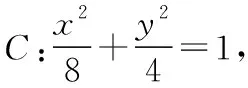
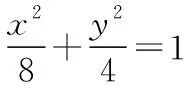
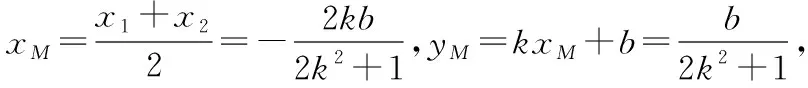
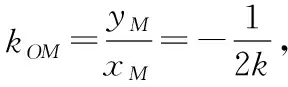
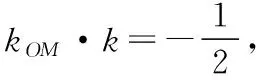
4.数形结合,偷梁换柱
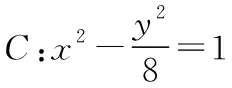
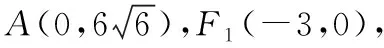
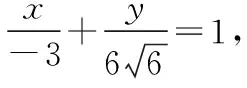
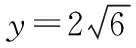
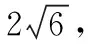
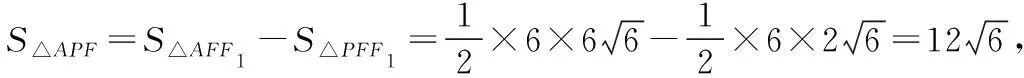

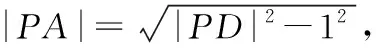
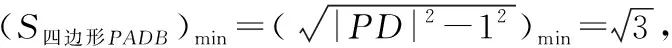
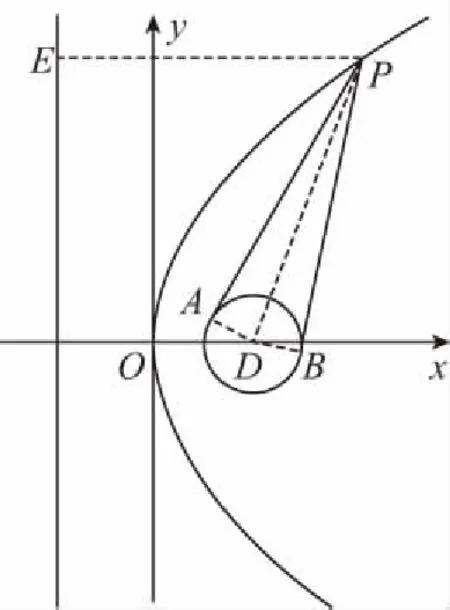
5.极端策略,围魏救赵


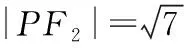
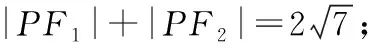

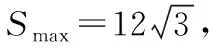
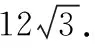
6.妙借向量,无中生有