遥控无杆飞机牵引车牵引转弯的运动学研究

解本铭 ，赵宏伟 ，王 伟 ，张 威 ，2

（1.中国民航大学 航空工程学院，天津 300300；2.中国民航航空地面特种设备研究基地，天津 300300）

1 引言

飞机牵引车是用来移动飞机的特种车辆[1]。无杆牵引车在作业过程中取消了牵引杆，利用特有的飞机机轮夹持举升装置，将飞机的前起落架夹紧、抱起后，使牵引车和飞机成为一个整体，实现飞机的牵引或顶推作业。国外的无杆牵引车发展迅速，较为知名的有德国汉莎航空公司与德国某制造商、美国的某公司、其中TLD在德国某工程公司和以色列航空工业公司（IAI）联合开发的TaxiBot已然更加智能化。国内飞机牵引车的研究起步相对较晚，但是也有不少厂家进行开发与制造[1-2]。牵引车在运动过程进行牵引或者顶推需要很高操作技巧，容易出现磕碰现象造成飞机延误或损坏。在有关牵引转弯轨迹方面的研究中，文献[3]提出了半挂汽车列车转弯模型，使半挂汽车列车的运动轨迹有了统一的描述并且给出了一种工程实用解法。文献[4]提出一种汽车及汽车列车在转弯过程中运动轨迹的作图法，以便在转弯过程去考察车辆的通过能力。文献[5]在分析车辆转弯时进行了横向轨迹控制仿真分析。关于飞机牵引系统转弯时如何在通过狭窄的通道时降低磕碰风险的相关性研究目前仍未见涉及。

基于现行飞机牵引车小型化、智能化发展趋势，提出一种小型遥控无杆飞机牵引车的结构布局。利用SolidWorks进行三维建模，将飞机前起落架（Nose landing gear，NLG）与机身结合处中心点（B点）与无杆飞机牵引车后驱动轮轴线中心点（C点）重合于同一竖直轴。将该牵引车与A320-200飞机组成牵引系统，同时利用ADAMS进行仿真分析，将所提出的B点重合方案与传统设计中B点不重合两种情况作对比研究，以翼尖扫过的半径和前起落架转过的角度两个参数为指标，分析其转弯性能的优劣。

2 遥控无杆牵引车的三维建模

以牵引车上放置前起落架左右轮胎中心为A点，前起落架与机身连接处中心点为B点，如图1所示。本设计的夹持举升机构可以使B点与两后驱动轮轴线中心点C重合于同一竖直轴线。当牵引车两后驱动轮以相同转速相反方向运动时，前转向轮通过偏转一定角度，使牵引车以B点或C点在xoy平面上的投影点为旋转中心进行旋转，飞机前机身理论上不会发生移动，提高了飞机牵引转弯时的操控准确性，避免磕碰事故的发生。

图1 A点、B点、C点在牵引车上的相对位置

Fig.1 The Relative Position of Point A、B、C Points on the Tractor

利用SolidWorks的三维建模功能，对新设计的无杆牵引车进行三维建模，图2中下挡板1与下挡板2用于夹持NLG两前轮，通过液压杆的伸缩，进而调整A点B点的相对位置，使B点与两后驱动轮轴线中心点C重合。

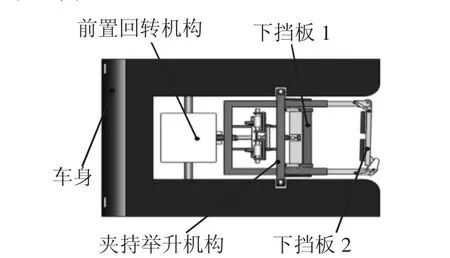
图2 遥控无杆牵引车的三维建模Fig.2 Three-Dimensional Modeling of Remote Control Rodless Tractor

在建立整车仿真模型时，是依照空客A320-200的前起落架轮胎的具体参数由内向外扩展设计的，主要技术参数，如表1所示。

表1 遥控无杆牵引车技术参数Tab.1 Technical Parameters of Remote Control Rodless Tractor

3 空客A320-200飞机模型与轮胎路面的创建

在SolidWorks中建立A320飞机模型，简化后的飞机模型包括：飞机机身、前起落架（包括两前轮）、主起落架（Main Landing Gear，MLG）包括4个后轮、以及转向系统等部件。为了方便计算，将飞机机身与左右主起落架固化成一个组件（不包括4个后轮）。最后按照实际飞机运动情况添加约束建立各个组件之间的连接。

牵引车轮和飞机轮都导入ADAMS中的轮胎模型；轮胎利用的是ADAMS中的uat.tbl文件，各个轮胎参数，如表2所示。

表2 牵引系统各轮胎参数Tab.2 The Tire Parameter of Traction System

与轮胎的创建类似，从ADAMS中导入路面；文件选择ADAMS文件中的2d_flat.tbl，创建长为160000mm、宽为80000mm的路面。

4 牵引系统与牵引路径的创建

在实际的无杆牵引作业中，夹持举升机构从接驳飞机前机轮之后，牵引车产生驱动力从前机轮传到NLG，进而传递到整个飞机，带动飞机主起从动机轮，牵引车与飞机形成一个整体—牵引系统。所以在建立牵引车与A320-200飞机之间连接时采用固定副，忽略前起落架左右飞机轮胎相对夹持举升机构的滚转与侧偏[6-8]。

为了使牵引车系统按照任意规定的路径行驶，可以通过matlab生成样条曲线的坐标文件，导入到AKISPL函数中进而成为可以被ADAMS内置控制模块所使用的曲线[9]。

设计出一个L型路径（下标为牵引路径的曲线），如图5所示。该L型曲线由两条长度为30000mm的直线及半径为13080mm的1/4圆弧组成。飞机在推出停机位后或由滑行道进入跑道时，通常会走L型路径。L路径有利于观察在转弯过程中本设计与传统设计的区别，以验证本设计的优点。

5 牵引系统在ADAMS中的仿真

为了验证B点重合情况下牵引系统转弯时的优点，相应的设置了B点不重合的情况（即将B点水平前移800mm，如图3所示）。以Douglas TBL-200为例，B点位置相对于设计的B点重合情况更为靠前。两种情况的具体说明，如表3所示。

通过计算可知A、B两点在xoy平面投影点相距356mm，A、B、C三点位置，如图3所示。

表3 B点重合和B点不重合情况Tab.3 Point B Coincident and Non-Coincident

当牵引车接驳NLG两机轮，围绕驱动轮轴线中心点C进行旋转时，由于B、C两点不重合，牵引车不会围绕B点旋转，直线AB与直线AC之间会形成一个变化的夹角，此时杠杆原理会对NLG施加影响，飞机前机身随之出现位移变化，所以设计B点前移的情况作为对比。

在飞机两侧翼梢小翼终端添加两个marker点，以此来记录飞机在转弯过程中的最大的范围。

轨迹3为牵引系统的牵引路径，如图4所示。2、4为飞机主起落架左右轮胎的运动轨迹；1、5轨迹为飞机两侧翼梢小翼终端点的运动轨迹。B点不重合情况下飞机翼梢小翼终端点的运动轨迹，如图 4（b）所示。

图4 B点重合与B点不重合两种情况下翼尖的运动轨迹Fig.4 The Tip Trajectories of Point B Coincident and Non-Coincident

为了更加清楚明了的观察两种情况在行驶过程中牵引系统的覆盖区域，将B点重合情况和B点不重合情况下飞机两侧翼梢小翼终端点的x、y、z坐标点导入MATLAB中进行对比分析。

导入MATLAB的坐标点只取x、y坐标舍去z坐标，如图5所示。放入xoy平面分析（即俯视图）。此处以翼尖轨迹半径作为评价指标是因为翼尖扫过的轨迹半径代表牵引系统转弯时能触碰到的最远距离，相比转弯的覆盖面积而言更直接准确。经过计算可得理想翼尖路径最大半径为30130mm、B点重合情况翼尖路径的最大半径为33633mm、

B点不重合情况下翼尖的最大半径为36436mm。可以得出B点不重合情况下翼尖半径超过理想值的20.9%，然而B点重合情况下只超过理想值的11.6%。可见B点重合情况下牵引系统更利于通过狭窄空间，从牵引系统开始进入弯道时刻，B点不重合情况相比B点重合情况发生的急转现象更剧烈；从弯道再进入直道时刻，前者相比后者更难以回正。

图5 两种情况飞机两侧翼尖轨迹对比图Fig.5 The Tip Trajectories of Point B Coincident and Non-Coincident

图6 B点重合时与B点不重合时的NLG旋转角度Fig.6 The NLG Rotation Angle of Point B Coincident and Non-Coincident

最后对两种情况的前起落架转弯角度做一个测试，如图6所示。B点重合情况下，前起落架转角最大值为25°；B点不重合情况下，前起落架转角最大值为32°；两种情况均不大于规定的±85°的极限值[10]，说明两种情况均在牵引的安全范围之内。以两图作对比可以反映出B点重合情况下牵引系统在转弯过程比较缓和，转角变化幅度不是很大；相反B点不重合情况在刚进入弯道和从弯道在进入直道时候会有急转现象，这两个时刻转角变化比较剧烈。从弯道进入直道的过程中B点不重合情况还出现了轻微的摇摆，而B点重合情况直接切入直道没有出现摇摆。

6 结论

（1）提出的一种小型遥控无杆牵引车，设计重点是夹持举升机构相对于牵引车车身的位置，使前起落架与机身结合处中心点与牵引车后驱动轮轴线中心点重合的方法减小了转弯时翼尖轨迹半径，进而降低了转弯时磕碰的风险。

（2）建立牵引路径通过SolidWorks三维建模，在ADAMS中进行仿真。将本设计与传统设计两种情况作对比，以翼尖扫过的半径和前起落架转过的角度两个参数作为评价指标，验证了本设计的优点。