“求学问,需学问”
朱国荣
数学教学中教师要想增强学生发现和提出问题的能力就应将培养学生“初步学会从数学的角度发现问题和提出问题”作为重要的教学目标,并能准确把握发现问题和提出问题的概念内涵,以开放的心态鼓励学生愿问、敢问,最终走向善问。那么,在具体教学实践中教师该如何操作实施?对此,本刊联合嘉兴地区七县市教研室围绕“小学数学教学如何培养学生发现和提出问题”展开了专题研讨,并刊登此专题研讨成果,供大家参考。
【摘 要】数学教学要增强学生发现和提出问题的能力,教师应将培养学生“初步学会从数学的角度发现问题和提出问题”作为教学重要目标,准确把握发现问题和提出问题的概念内涵,以开放的心态鼓励学生愿问、敢问,通过长期引导让学生善问,不断丰厚自身的学科素养,提升教学设计与实践能力。
【关键词】发现问题;提出问题;概念内涵;培养策略
诺贝尔物理学奖获得者李政道曾为嘉兴一所实验学校题词:“求学问,需学问,只学答,非学问。”因常去这所学校,所以常读到挂于研磨室墙上的这十二个字。初读时,乃至此后很长一段时间,这十二个字并没有给我留下深刻印象。直至近几年,随着修订后的数学课程标准将“两能”扩展为“四能”,将引导学生“初步学会从数学的角度发现问题和提出问题”列为数学课程重要目标之一,我才开始慢慢读懂这看似平常的十二个字所蕴含的深意。
反思当前的小学数学教学,最缺失什么?是数学知识、技能,是数学思想、方法,还是分析问题、解决问题的能力?最缺失的不是这些!而是我们的学生没有问题!
一节课临近结束,教师问学生“你们还有什么问题吗”,没有学生举手。教师等待、启发、诱导,依然没有学生提出问题。教师只能以“没有问题了,那我们就下课吧”草草收场。这样的情形屡见不鲜,以至于多数教师已经不愿意再这样问了。
反思教学,我们是否将培养学生发现问题和提出问题的能力定为教学目标,是否给学生创造了发现问题和提出问题的机会,是否为学生提供了发现问题和提出问题的材料?在不久前的一次教学调研中,我连续听了十多节数学课,竟然没有听到一次教师引导学生发现问题和提出问题的过程。李先生所担忧的“只学答”就是当前小学数学教学的普遍状态。
剖析当前的小学数学教学,可以毫不夸张地说,几乎所有的问题都来自于教师。是学生没有问题吗?当然不是!每一个孩子从牙牙学语开始,就经常问“为什么”,孩子天生就是会提问的。但为什么到了数学学习过程中,学生就突然没有了问题、提不出问题了呢?那是因为教师几乎不给学生提供发现问题和提出问题的机会,是因为教师害怕学生提出的问题不在预设之中,而干扰了既定的教学进程,是因为教师害怕无法回答学生提出的问题,而失去了教师的尊严和对教学的控制权。一句话,是因为教师害怕学生提出问题。
慢慢地,学生就开始习惯“只学答”,变得越来越不会提问、不敢提问了。偶尔有学生主动提出问题,也经常被教师忽视、回避,最后不了了之。以至于在不少学生看来,上课时提出问题就是在给教师出难题。
“只学答,非学问”,发现问题和提出问题的价值和重要性是不言而喻的。《义务教育数学课程标准(2011年版)》(以下简称《课程标准》)指出,学生自己发现和提出问题是创新的基础,要增强学生发现和提出问题的能力。爱因斯坦也曾说:“提出一个问题往往比解决一个问题更重要,因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想象力,而且标志着科学的真正进步。”
综上所述,引导学生发现问题和提出问题已经成为当前小学数学教学改革中一个十分重要和紧迫的课题,而且还是一个难题。
一、将“增强发现和提出问题的能力”作为教学重要目标
《课程标准》在总体目标中明确提出,要增强学生发现和提出问题的能力,培养学生初步学会从数学的角度发现问题和提出问题。这要求教师不应将引导学生发现问题和提出问题仅仅作为展开教学的一种手段,而应作为教学的一项重要目标。
如果仅将提问作为教学的一种手段,那么,即使教师让学生提出问题,也似叶公好龙一般,只期待学生提出教师需要的问题。这样的提问是假提问,只是借学生的口提出教师要的问题而已。一旦学生提出教师预设外的问题,提出一些似乎“不着边际”的问题时,教师就会手忙脚乱,不知所措,甚至产生严重的焦虑感和挫败感。
如果将提问作为教学的一项重要目标,那么,需要教师创设引导学生发现问题和提出问题的教学环节,给学生足够的观察、思考时间,鼓励学生从数学的角度提出有思考性、有价值的问题。需要教师以更加开放的心态面对学生提出的问题,不再以“预设之中”“有利于推进教学”作為价值评判标准。需要教师真正以学定教,善于根据学生提问状况展开教学。需要教师放下身段,敬畏学生,对未知问题、超出教学范围的问题采取更加包容的处理方式,坦承“不懂”,鼓励学生自己思考研究,这也是教学的应然状态。
二、准确把握发现问题和提出问题的概念内涵
发现问题和提出问题两者关系密切,但内涵不同。发现问题是指经过多方面、多角度的数学思维,从表面上看来没有关系的一些现象中找到数量或空间方面的某些联系,或者找到数量或空间方面的某些矛盾。而提出问题是在已经发现问题的基础上,把找到的联系或者矛盾用数学语言、数学符号表述出来。
发现问题是提出问题的基础和前提,提出问题是发现问题的深化和完善。当然,对于学生的学习过程而言,发现问题和提出问题是浑然一体、交织进行的。
学生发现和提出的问题是有水平层次之分的,一般可以分为模仿性问题和创造性问题这两个水平层次。模仿性问题是指学生根据已有的数学知识经验,模仿已有问题的样式提出的问题。模仿性问题通常就是一种习题,学生自己就能解答所提出的问题。创造性问题是指学生突破已有的知识经验,主动发现数量或空间方面的联系、矛盾,从而提出的问题。创造性问题具有三个主要特征:初次遇到的;对一般学生来说具有一定的挑战性;能促进知识的主动建构,能够生成新知识。
培养小学生发现和提出问题的能力,通常是从引导学生模仿性提问开始的。比如小学低年级教材中,在创设情境后,先由教师呈现一两个问题,学生作出解答后,再让学生照样子提出问题。但教学不能停留于引导学生模仿性提问,随着年级升高,教师要特别重视和鼓励学生提出创造性问题。哪怕是小学一、二年级,教师也不能只满足于学生提出模仿性问题。
我们来看下图中的这个例子(选自人教版二年级上册)。
在这个练习中,让学生模仿提出问题“每个篮球多少钱”并解答,并不困难。
但如果真正将增强学生发現问题和提出问题的能力作为教学目标,教学需要做一些改进。比如,教师可以将情境图经过处理后呈现给学生(如下图),鼓励学生观察、思考,从而创造性地提出问题。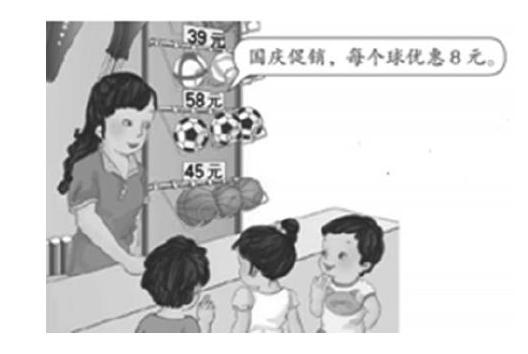
实践中,学生提出的问题有:
问题1:货架上有哪几种球?
问题2:“优惠8元”是什么意思?
问题3:“每个球优惠8元”是指每个足球优惠8元吗?
问题4:优惠后,每个足球多少元?
显然,这样教学,对学生提问能力的培养已经高于模仿性提问水平。其中最有价值的是“问题3”,这位学生为什么会提出这个问题呢?因为他发现图上“国庆促销,每个球优惠8元”这句话的对话框是指着足球“58元”。这确实是一个问题。一方面,如果要表示三种球都是每个优惠8元,那么,对话框应该指着营业员才合适。另一方面,学生还得思考“三种球每个的价格不同,都优惠8元,合理吗”,想明白这个问题,能为后续教学折扣问题积累经验。
上面这样的提问、交流、分析,看似跑题了,很多教师也会有疑惑:“这还是在教用退位减法解决问题吗?”深刻剖析,你会发现这就是对教学目标理解上的差异,站在培养学生发现问题和提出问题能力的角度,这样教学很有价值,学生的提问真正体现了思考性。
三、如何引导学生发现问题和提出问题
引导学生发现问题和提出问题,重点要研究两项内容,一是如何把握提问的时机,即研究哪些教学环节适合引导学生发现问题和提出问题;二是如何创设提问的情境,即研究创设怎样的情境,提供怎样的素材,能促使学生发现问题和提出问题。
(一)课始,根据将要学习的内容,鼓励学生发现问题和提出问题
课始引导学生提问,主要有两种方式。
(1)导学单提问或预学提问。先学后教是改变教学方式的重要策略,先学后教一般都会布置学生课前先学,或课始预学。通常采用的方式是设计导学单,引导学生展开自学。在导学单设计时,要设计两个大问题,一是通过自学课本,记录“你已经看懂了什么”;二是通过思考,记录“你还有什么问题”。教学时,不但要交流“看懂了什么”,还要交流“还有什么问题”,并将学生提出的问题作为展开教学的重要资源。
(2)看课题提问。这也是经常采用的提问方式,教师揭示课题后,马上引导学生看课题提问,从而了解学生的疑惑,梳理和呈现要研究的问题,起到目标导向作用。比如一位教师教学“百分数的认识”一课,板书课题后,就鼓励学生提出问题,实际生成的问题有:什么是百分数?百分数应该怎样应用?怎样比较百分数的大小?百分号怎么写?百分数和分数有什么区别?在学生提问的基础上,教师板书并梳理问题,教学也随着这些问题展开。
(二)课中,提供有结构的材料,引导学生发现问题和提出问题
在学生探究过程中,通过提供有结构的材料,鼓励学生从数学的角度发现问题和提出问题,是培养学生提问能力最为重要的途径,也是课堂教学过程中最具生命活力的部分。
(1)提供缺少明确的数学任务或数学问题的情境,要求学生根据其中的信息发现问题和提出问题。也就是在创设情境时,不要直接将问题呈现出来,而是鼓励学生自己根据情境中给出的信息和条件发现问题和提出问题。
例如,在教学二年级的“解决问题”时,教师呈现以下材料,引导学生提出问题。
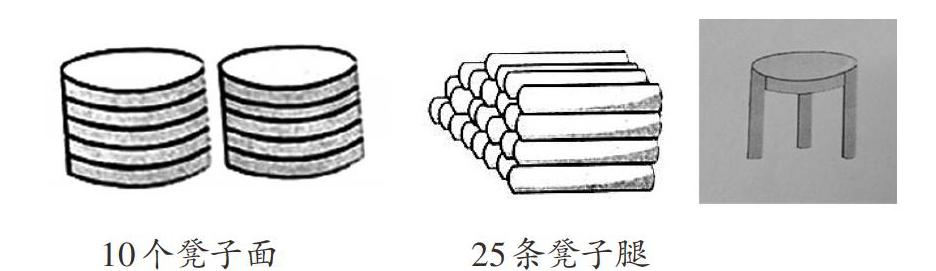
工人师傅想做些小凳子(如下图)。
10个凳子面 25条凳子腿
学生提出的问题有:
问题1:最多可以做几个小凳子?
问题2:如果要做10个小凳子,还少几条凳子腿?
问题3:为什么小凳子是3条腿的?
问题4:如果做成4条腿的小凳子,最多可以做几个呢?
其中“问题3”也是好问题,涉及四年级要学习的三角形稳定性的知识。
(2)提供结构不良的数学情境,引导学生发现问题和提出问题。结构不良的情境主要指情境中给出条件不充分、不清晰甚至有矛盾等。问题情境结构不良,反而会引发学生思考,促使学生产生疑问。
例如“百分数的意义”一课的教学,在引导学生初步认识百分数的含义后,教师创设了如下情境:
西塘八珍糕是清宫秘制的长寿补益食品,配方成分为:糯米粉39%;粳米粉35.1%。
情境呈现后,教师并没有让学生解读百分数的含义,而是直接引导学生提问。学生提出的问题有:
问题1:什么是粳米粉?
问题2:为什么糯米粉比粳米粉多?
问题3:为什么百分号前面是一个小数?
问题4:糯米粉和粳米粉一共占了74.1%,为什么不是100%?
在学生提问的基础上,教师抓住两个关键问题展开讨论。
为什么百分号前面是一个小数?让学生明白是因为将总量平均分成了100份,粳米粉的含量超过35份,又不到36份,所以用小数表示。
为什么不是100%?让学生推测还有其他成分,进而补充数据:白糖19.8%;山楂5.1%;其他1%。这时教师继续引导学生提问,学生提出的问题有:
问题5:为什么配方成分要用百分数表示?
问题6:为什么要写“其他1%”?
这也是两个十分有思考力的问题。展开对“问题5”的讨论,可以让学生體会百分数的优越性——方便比较的特点。在讨论“问题6”时,有学生认为是因为有些成分的含量很少,没有必要一一列出,也有学生认为这个“1%”就是西塘八珍糕的秘方所在……学生智慧地发现与表达,达成了数学思考和生活思考的和谐统一。
(3)呈现有结构的探究生成材料,引导学生发现问题和提出问题。在生成性课堂中,教师都会呈现学生探究生成的材料展开教学。一般的做法是,呈现材料后,引导学生自己解释,或者要求其他学生解读。着眼于培养学生发现问题和提出问题能力的教学,可以在学生对生成材料进行观察、思考后,先引导提问,再展开研究和讨论。
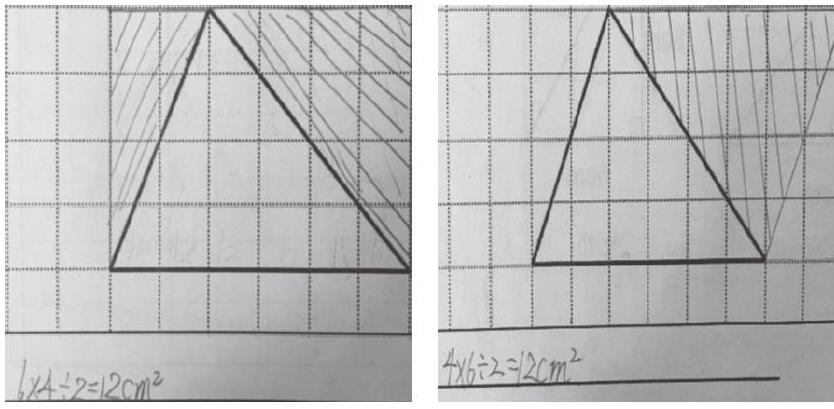
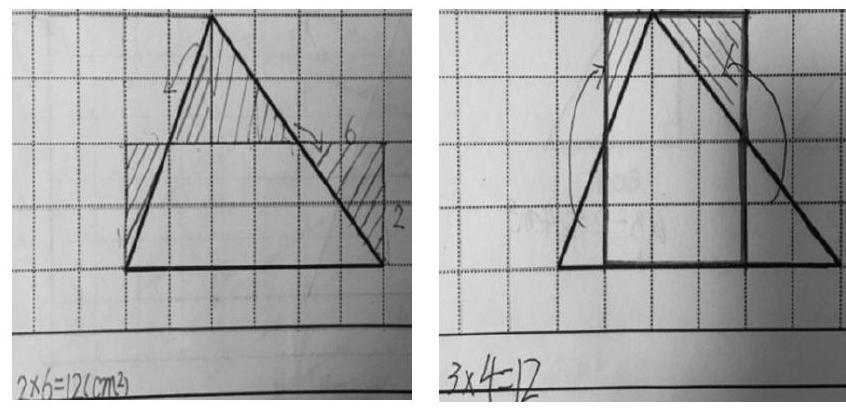
例如在教学“三角形的面积”时,教师给学生提供一个画在格子图上的三角形,让学生自己探索三角形面积的计算方法。反馈时,教师呈现以下生成材料,引导学生观察、思考,并提出问题。

学生提出的问题有:
问题1:为什么都要转化为长方形或者平行四边形?
问题2:转化的方法有什么不一样?
问题3:为什么后两个算式中都有“÷2”,而前两个算式中没有?
展开对这些问题的讨论,学生不但深刻理解了三角形面积的计算方法为什么是“底×高÷2”,形成了丰富多元的表象,还很好地渗透了转化思想方法,发展了学生的空间观念。
(三)课尾,或者解决一个问题后,鼓励学生发现和提出想要进一步研究的问题
分析问题、解决问题并不是学生数学学习的终点,教学并不是要把“有问题”的学生都教成“没有问题”的学生。教学的重要意义是不断让学生在解决问题的过程中发现和提出新的问题。
解决完一个问题后,教师可以引导学生利用“否定假设法”来提出问题——如果它不是这样的,那又可能是什么呢?
例如“数与形”一课的教学,在引导学生借助形研究了从1开始的连续奇数的和的计算方法,掌握了怎样借助正方形数的特点确定项数的方法后,教师引导学生继续提出问题:解决问题后,你还有新的问题吗?学生提出了如下问题:
问题1:除了正方形数,还有长方形数、三角形数吗?
问题2:从2开始的连续偶数的和怎样计算?
问题3:不是从1开始的连续奇数的和,怎么求?
问题4:2+6+10+14+……这个数列的和,怎样求?
课堂上,限于时间,教师选择“问题2”让学生展开研究,并将其他的问题展示在班级“问题墙”上,鼓励学生课外自主研究。
最后,还需要说明的是,从课前、课中、课尾三个时间段来阐述,只是想提示教师要选择比较合适的教学时机创造发现问题和提出问题的机会,课前和课尾是“常规时段”,课中是“主要时段”。就某一节课而言,只要求教师能有意识地给学生创造一些提问的机会,呈现一些适合提问的材料,并不是要求全部问题都让学生提出来,这不可能,也办不到。细水长流,持之以恒,才能有效增强学生发现和提出问题的能力。引导学生提出猜想、互相质疑也都是提出问题的一部分,需要教师随时关注,智慧引导。
“求学问,需学问”,要增强学生发现和提出问题的能力,培养学生初步学会从数学的角度发现问题和提出问题,这并不容易。不但要求教师以开放的心态鼓励学生愿意提问、敢于提问,通过长期引导让学生善于提问,还要不断丰厚自身的学科素养,提升教学设计与实践能力。
(浙江省嘉兴教育学院 314000)

