解析几何变式问题制作的一种方法

梁海艺　吴跃忠

(华南师范大学数学科学学院　510631)

变式训练是解题训练的重要手段，合理选择变式训练材料可提高变式训练质量，然而，如何选择符合学生数学现实的变式训练题颇不容易，本文提供一种制作变式问题的方法，钻研该方法，不仅可以获得丰富的变式命题，还能帮助我们深刻理解变式问题内在本质，以及优化与变式问题相关知识结构.本文通过对一道高考试题的条件结构改变，获得不同难度水平的变式问题.

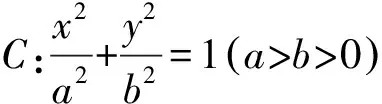
(2)在椭圆C上，是否存在点M(m,n)使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A,B，且△OAB的面积最大？若存在，求出点M的坐标及相对应的△OAB的面积；若不存在，请说明理由.

此题的条件分别属于三个条件(见下列集合中黑体字)：

类别集A={椭圆，双曲线，抛物线，圆}，

解几知识集B={离心率，轨迹，点(包括顶点、焦点、动点、定点、公共点、交点、中点、对称点、内心、外心、重心、垂心等)，弦(包括各类直线：准线、渐近线、对称轴、动直线、定直线、切线、垂线、平行线等)，距离(包括焦距等)，面积等}，

非解几知识集C={最值，极值，配方，定值，参数取值范围，向量数量积等}.

对上述三个集合中元素合理选取，可得到不同的变式问题.

1　近迁移解几变式命题制作

如所知，变式是通过改变原命题非本质条件以获得新命题，如果变式与原命题距离较短，其迁移量不大，则可以利用下面方法.

1.1　条件替换

制作变式试题时，只需要将原题设条件与其所在集合中元素(条件)互换就形成新变式题，可以改变一个条件，也可以改变多个条件.

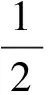
如改变二个条件，在集合A中，将原题设条件的“椭圆”和“圆”替换成“圆”；在集合C中，将“面积最大值”改换为“向量数量积最值”，有

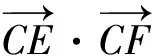
在集合A中，将原题设条件“椭圆”和“圆”替换成 “抛物线”，将“面积最大值”改换成集B中“线段中点轨迹”，有

变式3(2013辽宁理20)抛物线C1:x2=4y,C2:x2=-4y，点M(x0,y0)在抛物线C2上，过M作C1的切线，切点为A,B(M为原点O时，A,B重合于O).当M在C2上运动时，求AB线段中点的轨迹方程(AB重合于O时，中点为O).

1.2　位置替换

位置替换，指的是上述三类集合中，将原题设中动点运动区域替换成新的区域，如在集合B中条件元素(如，平面内某一动点，某直线上的动点)的替换.位置替换也可在条件替换的基础上进行，所形成的变式中既涉及条件替换也涉及位置替换.

如，在类别集A中，将原题设条件的 “圆”替换成“椭圆”，在集合B中，将动点M的位置替换成在“y轴”上，可获得以下变式：

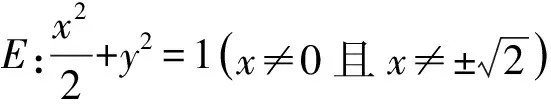
将原题设条件的 “圆”替换成所在类别集A中的“抛物线”，将动点M的位置替换成在其所在集合B中的“直线l:x-y-2=0”上，可获得以下变式：

变式5(2013广东理20)设P是直线l:x-y-2=0上的点，过点P作抛物线C:x2=4y的两条切线PA,PB，其中A,B为切点.当点P在直线l上移动时，求|AF|·|BF|的最小值.

将原题设条件的 “圆”替换成所在类别集A中的“椭圆”，将动点M的位置替换成其所在集合B中的“椭圆外”，可获得以下变式：

2　远迁移解几变式命题制作

制作变式跨度比较大的命题，则可通过选择上述集合C中的一个或多个元素，使得变式题难度加大.

2.1　问题替换

问题替换指的是原题设条件保持基本不变或进行了近迁移，再选择集合C中的一个或多个元素来替换原命题的问题形成新变式题.

如选择集合C中“取值范围”，可在原题设条件的基础上，确定某一变化的几何量，以其“取值范围”来替换原题设问题中“面积最大”，如下列变式：

如选择几何量“离心率取值范围”，保持原题设条件不变，考虑对原命题进行逆向变式，以“未知具体曲线”替换原题设已知曲线条件，命题问题替换成“离心率的取值范围”，作如下变式：

如选择集合C中的“向量数量积”“取值范围”，原题设条件保持不变，以其“向量积的取值范围”来替换原题设的问题“面积最大”，形成如下变式：

如选择 “向量数量积”作为题设的问题时，在近迁移的基础上(即用“双曲线”替换原命题的“椭圆”)，再将“特殊的向量数量积”等价替换原命题的问题“面积最大”，形成如下变式：

2.2　位置替换

与近迁移中的位置替换法一致，但在这里，位置替换一般在问题替换的基础上进行.

如选择集合C中的“向量积”、“等比数列”和“取值范围”，将原题设条件中动点M的位置替换成在“椭圆内部”，增加“等比数列”作为题设条件，以“数量积的取值范围”替换原命题的问题“面积最大”，可获得以下变式：

3　创新解几变式命题制作

创新变式命题指的是 ，该命题的题设条件中具有课本以外知识.此处考虑增加一个条件集合D，其中的元素为文献资料中关于圆锥曲线的超越了课本知识的性质，即

第四类为性质条件，D={文献资料中关于圆锥曲线的超越了课本知识的性质}.

创新变式命题制作方法：先选择圆锥曲线的一些相关性质，然后将原题设条件与性质中的条件元素进行替换，形成新变式题.

本文仍从原命题出发进行创新变式命题制作，以下介绍集合D中几个相关性质作为变式的条件或背景，以便变式命题的制作.

性质4[4]二次曲线上四个不同点A,B,C,D共圆的充要条件是这四点组成的四边形两对角线所在直线的倾斜角互补.

以下几道变式题分别是性质2—性质4的变式应用：

变式16在直线l:x=m(m<0)任取一点M(m,n)，过点M分别作抛物线E:y2=4x的两条切线，切点分别为A,B.

(1)证明：直线AB恒过定点E，并求出该定点坐标；

(3)直线l上是否存在点M(m,n)，使△MAB为等腰直角三角形，若存在，求出点M的坐标及相对应的△MAB的面积；若不存在，请说明理由.

将集合A、集合B、集合C和集合D中的知识与原命题条件更换，可以形成几乎取之不尽的变式问题，值得注意的是，根据上述集合内元素知识替换形成的变式问题，具有探究性质，其真假性尚需进一步判断.本文制作的变式问题，皆为真命题.