核心素养怎样考(一)

李尚志

(北京航空航天大学　100083)

大家都承认郎平是优秀的女排教练.凭什么理由承认? 看郎平写的关于怎样当教练的论文吗? 即使看了也看不懂.也不用看.只凭一条就够了: 郎平带领中国女排力克群雄,勇夺冠军.排球教练在制定计划的时候也许应该提出很多的理论,做出很多的论证和分析,来说服别人支持她的训练方案.但最终的说服和检验只有一条: 带领队员打赢比赛，夺得冠军.

数学也是这样.要论证某种教学方式的正确性和有效性,也许应该根据核心素养的要求进行论证.但最终检验学生核心素养的高低，不是让学生写核心素养的论文,而是让学生做数学题.会做数学题不一定说明核心素养高,但核心素养必须通过解决数学问题来体现.那就要看做什么样的数学题, 是怎样做出来的.

要说明这个道理, 也不能空口说白话.以下是我在中国科学技术大学和北京航空航天大学的自主招生和选拔优秀学生的考试中实际出过的一些真题(见文后附：测试题1).下面我就具体解释, 为什么要出这些题? 考察学生什么样的核心素养.有人对此不屑一顾, 心想: 何必要什么核心素养.我只要训练学生一套题型就能对付任何考试.那就欢迎把你的题型拿出来对付我的考试.

比如说, 以下第1题你训练什么题型?

一、填空题

1.设(x1，y1)，(x2，y2)，(x3，y3) 是平面曲线x2+y2=2x-4y上任意三点.则A=x1y2-x2y1+x2y3-x3y2的最大值为.

题型是有的.但中学老师一般都不训练, 因此我才要考.我希望所有的考生都没有被训练过, 大家都在同一条起跑线上起跑, 一律平等.假如大家都没有训练过, 都不会做.怎么起跑?

放弃与选择: 这道题考的第一条素养是: 遇到不会做的题怎么办?

遇到不会做的题, 最简单易行的办法是: 跳过去先做会做的题, 会做的题目做完了,该拿到的分数拿到了, 再来想不会做的题, 多想出一道就多一份意外收获.

但是, 有很多自以为聪明的考生不这么办.他们认为天下没有自己不会做的题, 遇到不会做的题也不肯放弃.还有的老师认为: “ 要想让未成年人在短时间内判断自己不会, 并且大胆放弃, 这本身就是一件很困难的事情.” 我无法理解这种逻辑.如果一个未成年人不会做某个题,强迫他一定要做出来, 这才是很困难的事情.反过来, 暂时放弃不会做的题, 先做会做的题, 不应该有任何困难.只要在做题, 把题做出来了,就不是放弃而是得到.在难题面前耗费过多的时间, 没有时间做会做的题目, 该得的分丢掉了, 这才是更大的放弃.

我把难题放在前面, 就是要考查哪些学生头脑更清醒, 更懂放弃,更会选择.这样的素养不仅对考试有用, 对一辈子的生活和工作都有用.如果通过考试能让一部分糊涂人吃了亏有所醒悟, 也是一桩功德.

不过, 我把难题放在前面的主要目的还不是逼大家都放弃, 而是要给敢于绕过障碍胜利前进的考生额外的奖励, 让他们有机会乘胜返回，扫除障碍.虽然第1 道题就不会做, 第2道题也不会做.哪怕前10道题都不会做.但只要坚持下去不气馁, 总会遇到会做的.比如, 第11题解答题应该有办法做.

二、解答题

11.已知: 平面直角坐标系中两点A,B的坐标分别为(a1，a2),(b1，b2).O是原点.将OB沿顺时针方向旋转直角得到OB′.

(1) 求△OAB的面积.

解法1求△OAB的面积S△OAB并不难.用的知识最少的方法是: 从A,B分别向x轴作垂线交x轴于C,D, 将△OAB面积写成

S△OAB=S△OBD+SDBAC-S△OAC

这个方法对图上画的A，B的位置是正确的.但缺点是：假如A，B的相对位置有变化,a1，a2，b1，b2相互之间的大小、正负关系有变化, 还应根据不同情况讨论其中各个数的正负.

解法2题目只要求△OAB的面积.已知条件却叙述了一句:“将OB沿顺时针方向旋转直角得到OB′.” 看起来与△OAB面积无关.如果你觉得它真的与△OAB面积无关, 可以置之不理.但如果你把它考虑在内, 却能够给你一点启发.

正弦变余弦,面积变点乘

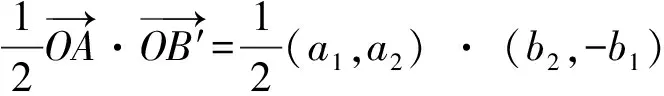
公式就是套路.不过, 训练专家很可能没训练过这个公式, 对这个公式推理过程中有一个环节也很可能不熟悉: 怎样由B(b1，b2) 的坐标算出顺时针旋转直角之后到达的点B′的坐标(b2,-b1).本文建议两个方法.一个用现成套路，另一个不用套路, 自己凑答案.

有人认为解方程求出x，y才是“通法”.凑出来的都是左道旁门.由

0=b1b2-b2b1=(b1，b2) · (b2,-b1)

解法3解法1太原始, 解法2太巧妙, 都不容易想到.有一种方法容易想到: 直接求△OAB的底和高来算面积.

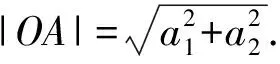
底边OA上的高|BH| 就是B(b1，b2) 到直线OA的距离, 直线OA的方程为a2x-a1y=0.利用点到直线的距离公式算出

三角形面积

不管用哪一种方法, 或者你还有别的方法, 得出的答案

x2-2x+1+y2+4y+4=5

⟺(x-1)2+(y+2)2=5,

要把第1题说清楚, 还需要搞清楚第11题面积公式中a1b2-a2b1正负号的意义.解法2把这个问题讲清楚了:

D=a1b2-a2b1的绝对值等于△AOB面积的2倍, 也就是以OA，OB为邻边的平行四边形的面积.而D的正负号就是sin ∠AOB=cos ∠AOB′的正负号: 当∠AOB∈ (0，π) 为正, ∠AOB∈ (-π，0) 为负.假如将角AOB的大小限定在[0，π] 的范围内, 由OA到OB是逆时针方向旋转则为正, 顺时针方向为负.第1题要使A取最大值, 当然就需要x1y2-x2y1与x2y3-x3y2都为正.这很容易做到, 只要圆内接正方形四个顶点O(0，0)，P1(x1，y1)，P2(x2，y3)，P3(x3，y3) 的旋转方向都是逆时针方向90° 就行了.

借题发挥:二阶行列式

第11题推出的公式

是不是现成套路? 教科书有吗? 当然有.所有的线性代数教科书都有

叫做二阶行列式.却很少有教科书讲它的几何意义是平行四边形面积,三角形面积的2 倍.为什么不讲? 很难讲懂吗? 参加我的考试的中学生可以在考场上临时把这个面积公式推出来, 而且马上用来解题得分,这能算难吗?

如果要说难, 三阶行列式肯定比二阶行列式更难.可是所有上过大学的人(包括大学生和中学教师)都知道三阶行列式代表平行六面体体积, 却有很多人不知道二阶行列式是平行四边形面积, 原因何在? 三阶行列式的几何意义是空间解析几何课程讲的, 按道理应该在平面解析几何课程讲二阶行列式是平行四边形面积, 可是却不讲.线性代数讲n阶行列式更不讲几何意义, 就都没有地方讲了.当然高考也不考.高考不考不要紧, 自主招生可以考.比如我就考了, 把能够自己推公式并用来解另外一道题的学生录取进来, 做不到这点的淘汰掉.

有些人老是把应试教育和核心素养对立起来, 把死记硬背和灵活应用对立起来.其实,应试与死记硬背也都是素养.能够死记硬背现成公式用来解决现成模式的问题, 就是数学核心素养中的“数学运算”.而能够用现成公式加以变通解决不现成的问题, 就是数学核心素养中的“数学建模”.高考以死记硬背为主, 稍微来几道灵活应用的, 让死记硬背的考生能够考上一般大学, 让灵活应用的考生考上名牌大学.所以你不能逼着所有考生都灵活应用, 他们反正也不想考名牌大学,你逼也逼不出来, 何必拔苗助长呢? 只要出点高考难题或者再由名牌大学出点自主招生难题把他们淘汰掉就行了.大家各得其所, 各上各的学校,培养不同档次的人才.适应不同社会岗位的需要.

附：测试题1

一、填空题: (10个小题共90分, 每小题9分)

1.设(x1，y1)，(x2，y2)，(x3，y3) 是平面曲线x2+y2=2x-4y上任意三点.则A=x1y2-x2y1+x2y3-x3y2的最大值为____________.

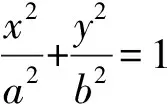
4.多项式(xsin 75°+sin15°)2012被x2+1除, 余式为__________.

5.平面上建立了直角坐标系,A,B是平面上两点.将OB绕原点O旋转直角到OB′.已知A,B′的坐标分别是(3,1) 与(-2，2).则点B到直线OA的距离为________.

6.将空间直角坐标系的坐标轴绕某条直线旋转, 使Ox轴旋转到Oy轴,Oy轴旋转到Oz轴.则旋转角度是________.(求最小正角)

7.在正方体ABCD-A′B′C′D′中,P是侧面BB′C′C内一动点, 若P到直线BC与直线C′D′的距离相等, 则动点P的轨迹所在的曲线是________.

8.某商场抽奖, 中奖率为10%.以下第______件事情发生的概率更大.

(1) 只抽一张就中奖.

(2) 连续抽20张, 全部都不中.

10.方程x3=-i的全部解为______

(提示: 利用棣美弗公式(cosα+isinα)n=cosnα+isinnα.)

二、解答题(3个小题共60 分, 每题20 分)

11.已知: 平面直角坐标系中两点A,B的坐标分别为(a1，a2), (b1，b2).O是原点.将OB沿顺时针方向旋转直角得到OB′.

(1) 求△OAB的面积.(2) 求∠AOB的角平分线上全部点的坐标.

12.在一次智力测验中, 老师给出了某个数列的前两项1,2, 让学生填写第3项a3.有的学生填写a3=3, 有的学生填写a3=4, 老师均判为正确.另有一个学生填写a3=0, 你认为正确吗? 如果你认为正确, 试给出数列的通项公式an=f(n) 使它的前3项f(1),f(2),f(3) 分别等于1,2,0.

如果数列的前99项依次为1,2,…,99, 能否给出通项公式使第100项等于2013?

13.英文加密: 将26个英文字母a,b,c,…,y,z依次用整数0,1,2,…,24,25 代表.设某个字母用整数X代表, 则3X+7 被26 除得到的余数代表的字母就是被加密后的字母.将英文原文的每个字母用这个方式加密, 就得到密文.

(1) 将原文day加密成密文.

(2) 根据密文zaj求原文.