对数学问题2251号的探究
陈 清 钟建新
(江西省赣州师范高等专科学校 341000)
1 《数学通报》2251号问题引发的思考
《数学通报》2015年7月号问题2251为:如图,已知△ABC中∠A,∠B,∠C的对边为a,b,c,设P是△ABC内一点,若∠PAB=∠PBC=∠PCA,求证:

对数学问题2251,提供人刘老师利用正弦定理结合相关的几何结论给出了证明.其实点P就是几何中常说的勃罗卡点,一个数学中经典的几何点.
从19世纪的最后20多年,在欧洲曾出现过一阵对勃罗卡问题的研究,可谓成果累累,其中等式cotα=cotA+cotB+cotC(α为△ABC的勃罗卡角)就是当时提出的关于勃罗卡点的一个基本性质.
近些年来,国内的数学刊物陆续刊登了一些勃罗卡问题方面的文章,如《数学通报》杂志分别在1993年第3期、2000年第5期、2010年第12期、2014年第7期刊登了《勃罗卡点的一个计算公式》、《勃罗卡角计算公式》、《一个奇妙的向量恒等式》、《与勃罗卡相关的一个几何最值问题》四篇论文,可见勃罗卡问题是初数研究的好素材,对它的研究经久不衰,成果给人启迪.基于此笔者另辟蹊径,从问题2251出发, 得出与勃罗卡点关联的不等式,可以说是对该问题的新探究.
2 2251号问题的探究
定理1已知△ABC中∠A,∠B,∠C的对边为a,b,c,设P为△ABC的勃罗卡点,则

证明由文[1]知

要证不等式(1)须证
不妨令x=a2,y=b2,z=c2,则等价于证明
⟺y3z2+y2z3+z3x2+z2x3+x3y2+x2y3-2x2y2z-2xy2z2-2x2yz2≥0
⟺y3z2+y2z3+z3x2+z2x3+x3y2+x2y3
≥2x2y2z+2xy2z2+2x2yz2.
我们知道
y(yz-yx)2+z(zx-zy)2+x(xy-xz)2≥0,
整理得
y3z2+y2z3+z3x2+z2x3+x3y2+x2y3
≥2x3yz+2xy3z+2xyz3.
又据平凡不等式x2+y2+z2≥xy+yz+zx,
两边同乘2xyz,可得
2x3yz+2xy3z+2xyz3≥2x2y2z+2xy2z2+2x2yz2,
从而不等式(1)得证.
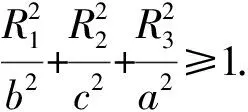
证明记△ABC的外接圆半径为R.因为P是△ABC的勃罗卡点,
设∠PAB=∠PBC=∠PCA=α,
则∠BPC=π-α-(C-α)=π-C,
据Cauchy-Schwarz不等式、熟知的不等式
∑a2≤9R2及均值不等式得

笔者进一步从勃罗卡点引申到三角形内任一点,得到与问题2251关联的新结论.

证明由文[2]Klamkin惯性极矩不等式可得
记x=a2,y=b2,z=c2,则要证不等式(2)只要证明
则不等式(2)得证.


因(ab-c2)2≥0,则(ab-c2)2=b2c2+c2a2+a2b2-c2[(a+b)2-c2]≥0,
又4rarb=(a+b)2-c2,
上述三式相加得

