美国早期代数教科书中的根式定义*

栗小妮　汪晓勤

(华东师范大学教师教育学院　200062)

1　引言

16世纪法国数学韦达(F.Viète, 1540～1603)在他的《分析引论》中使用字母表示未知数和已知数，使得数学从缩略代数阶段进入符号代数阶段[1].用字母表示数的使用大大方便了数学的表达和运算，但也产生了一些问题.在19世纪末实数理论体系建立后，数学家对数进行了严格的定义和分类，但由于“式”的本质用途在于简便表达和运算，所以并无一致的分类.

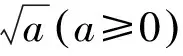
数学教育研究表明，学生对数学概念的理解过程与数学概念的历史发展过程具有一定的相似性，历史上数学家所遭遇的困难往往正是学生所经历的学习障碍.匈牙利著名数学家和数学教育家波利亚(G. Pólya, 1887～1985)曾指出：“只有理解人类如何获得某些事实或概念的知识, 我们才能对人类的儿童应该如何获得这样的知识作出更好的判断.”[5]荷兰数学家和数学教育家弗赖登塔尔(H. Freudenthal, 1905～1990)也有类似观点，称“年轻的学习者重蹈人类的学习过程, 尽管方式改变了”[6].美国数学史家M·克莱因(M. Kline, 1908～1992)也说：“历史顺序是教学的指南.”[7]有鉴于此，本文对1830-1929一百年间出版的81种美国代数教科书中有关根式内容进行了考察，试图回答以下问题：美国早期代数教科书是如何定义根式的？定义是如何演变的？根式定义的历史对我们今天认识二次根式有何启示？对今日二次根式概念的教材编写和课堂教学又有何启示？

2　研究对象

我们共选取20世纪中叶之前出版的81种美国代数教科书，其中70种为中学教科书，11种为大学教科书.若以十年为一段，则各教科书的时间分布情况如图1所示.其中，对于同一作者再版的教科书，若内容无显著变化，则选择最早的版本，若内容有显著变化，则将其视为不同教科书.81种代数教科书均将有关“根式”的内容单独列为一章，其中有68种在定义后给出了用来进一步解释定义的例子，约占84%.

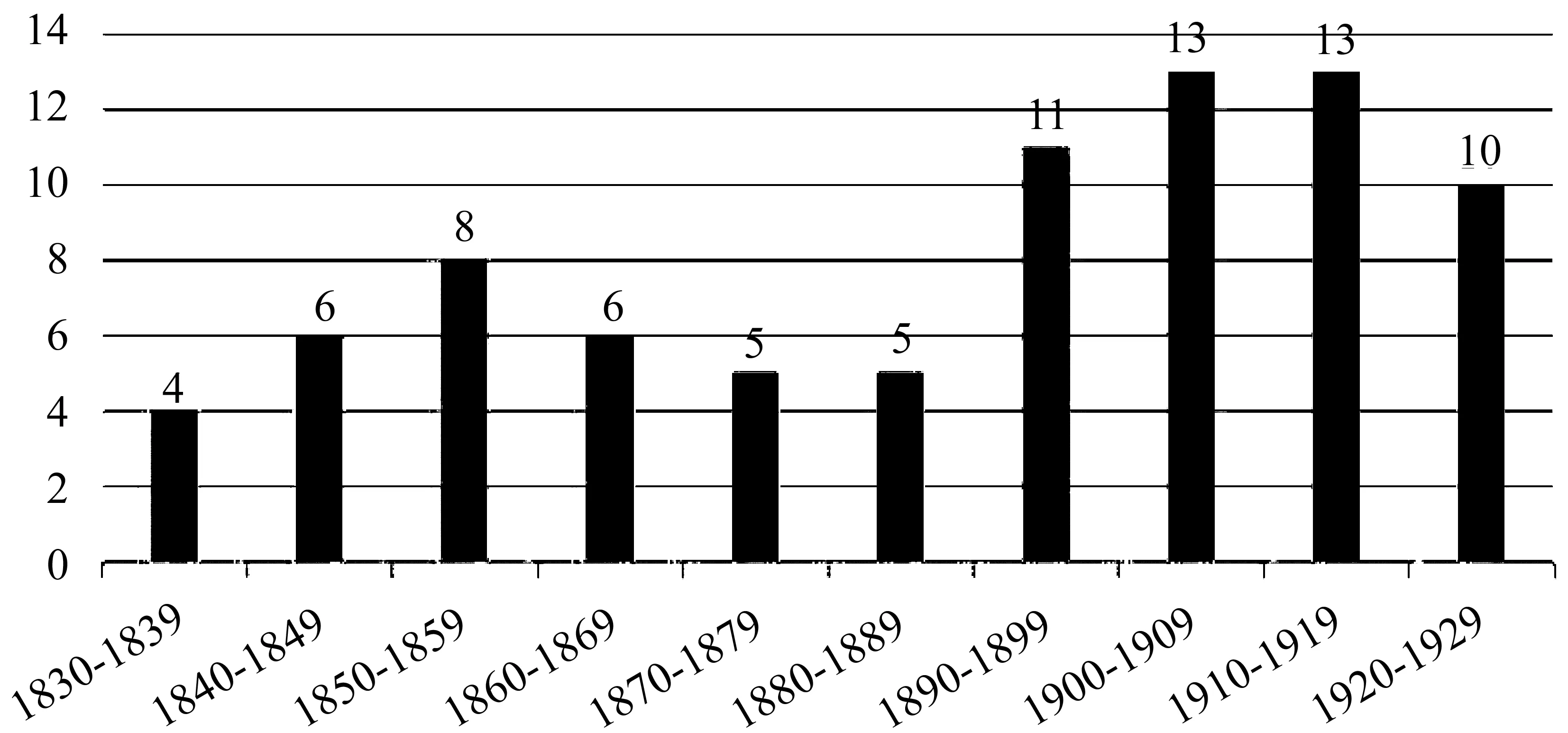
图1　81种教科书的时间分布

3　根式的定义

在美国早期教科书中，“根式”一章的主要内容均为平方根、二次根式、分数指数幂及其运算.实施开方运算后的式子有两种名称，一种为根式(radicals)，一种为不尽根式(surds).一些教科书对根式和不尽根式均作了定义，一些仅定义了根式或仅定义了不尽根式.若以20年为一时间段，图2给出三种定义方式的时间分布.

图2　三种定义方式时间分布

3.1　仅定义根式

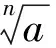
3.2　仅定义不尽根式

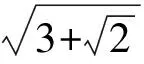
3.3　分别定义根式和不尽根式

对根式和不尽根式分别作出定义的教科书有68种，约占84%.经过详尽统计和分析发现，这些定义又可以分为两类，一类将根式等同于不尽根式，共19种，约占28%；一类对两者进行了严格区分，共49种，约占72%.表1给出的是等同定义的典型形式.

表1　不区分根式与不尽根式的典型定义

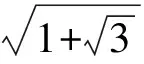
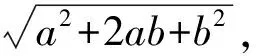
表2　区分根式与不尽根式的典型定义

3.4　无理式的定义

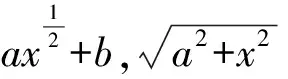
3.5　若干特点

在我们所考察的81种美国教科书中，根式的定义有以下特点.

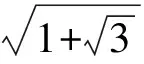
4　根式定义的演变

从仅定义根式或者仅定义不尽根式的处理方式中，无法看出作者对根式和不尽根式关系的认识.对于同时定义两者的教科书，我们以20年为一时间段，对两种不同的认识作了统计，图3给出了统计结果.

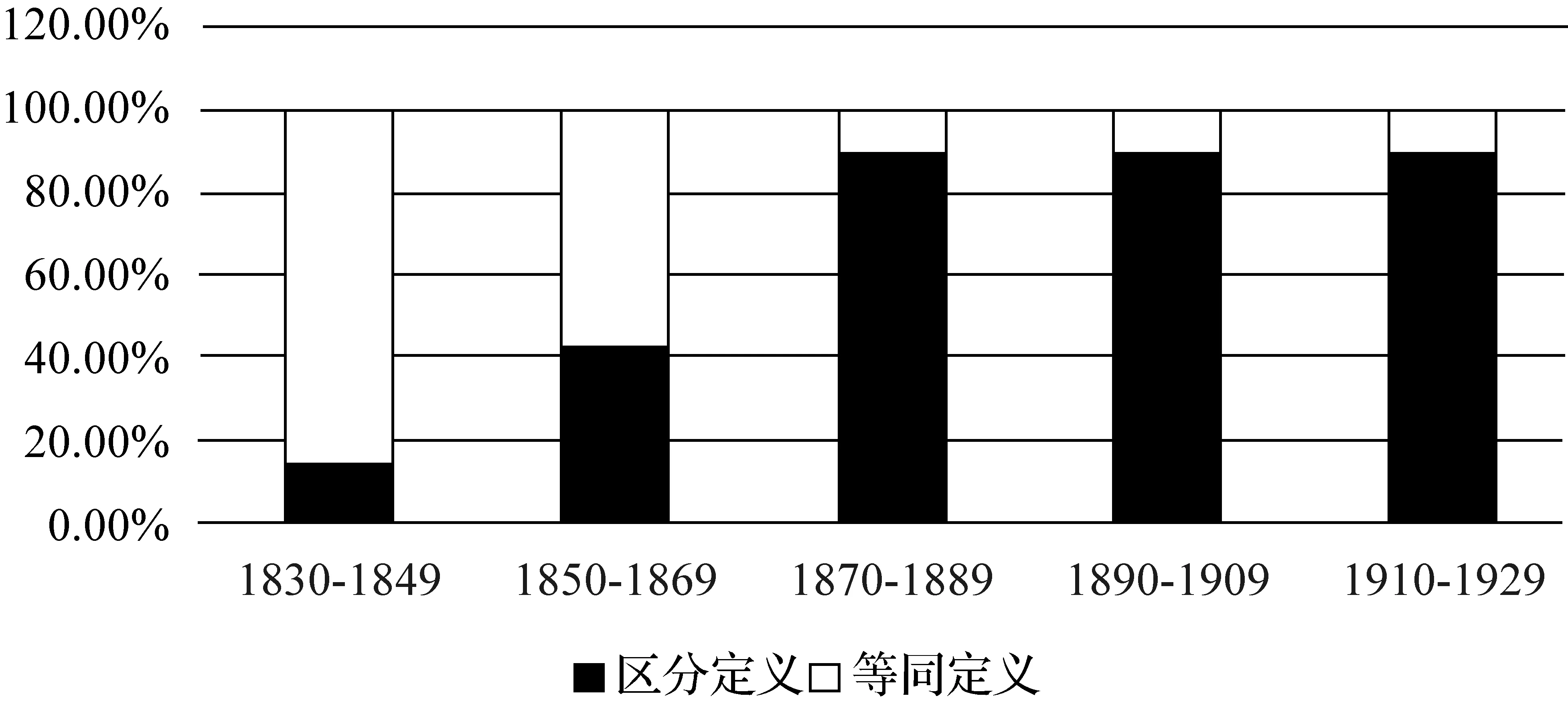
图3　教科书对根式与不尽根式关系的不同认识的时间分布

从图3中可以看出，在我们所考察的时间段内，早期的教科书大多将根式等同于不尽根式，而随着时间的推移，持这种认识的教科书逐渐减少，对两者作出严格区分的教科书逐渐增加，最终，绝大多数教科书将两者区分开来.这一点也可以从仅定义根式(radical)的7种教科书的两个不同时间段的不同特征得到佐证.

5　结论与启示

5.1　对教科书编写的启示

5.2　对教学设计的启示