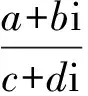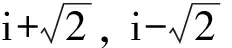核心素养怎样考(二)
李尚志
(北京航空航天大学 100083)
再来看测试题*测试题1见《数学通报》2018年第3期P4,文中所写题号均对应测题1.第2题.

有一年高中数学联赛考过椭圆的内接菱形的最大面积. 但没考过内接三角形、四边形, 更没考过内接8边形. 怎么做? 设8个顶点的坐标(xi,yi) (1≤i≤8) 表示出面积, 再求16元函数的最大值? 太复杂.
只能先放弃. 等到以后再说. 一直等到:


图1


核心素养:数学抽象
在北航参加过考试的很多学生考试结束后告诉我: 他们参加过奥数培训, 都知道椭圆面积是πab, 早就背得烂熟. 他们疑惑不解的是: 既然大家都背熟了椭圆面积, 填空题也不需要讲理由, 为什么老师还要给提示? 我反问: 奥数培训过椭圆内接8边形的最大面积吗? 你们知道那道题的答案吗? 很多同学说不知道答案. 我说太可惜了. 我用这道题来提示那道题. 可惜你们拒绝了这个送上门来的提示.
第9题的提示是将椭圆拉成圆, 利用圆面积计算椭圆面积. 这个原理也可以用来解填空题的第2题, 同样地把椭圆拉成圆, 利用圆内接8边形的最大面积来计算椭圆内接8边形的最大面积.

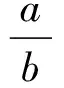

很多学生和老师认为, 既然是填空题, 只要答案对了就行, 不必知道理由. 只需要知其然, 不需要知其所以然. 如果考问答题, 不知其然要扣分. 计算题只写答案不写步骤要扣分, 有的步骤可能还要写理由,不写或者写错了也要扣分. 步骤和理由都是所以然. 证明题更是专门写理由讲所以然的. 我这里是填空题, 只要答案正确就得满分, 不知道理由不扣分. 第9 题的9 分全都给你. 也许你觉得心满意足了.
不过, 第2题的9分被我扣了, 因为你做不出答案. 第9题你可以死记硬背现成答案, 第2题没人告诉你答案, 你自己也想不出来, 就丢分了.也不是没人告诉, 我写了一个提示教你做第2题, 你拒绝听, 就只好丢分了. 为什么拒绝?因为我的提示不是写在第2题而是写在第9题, 不是告诉答案而是提示思路, 不是提示第2 题而是提示第9 题. 不是让你知其然而是让你知其所以然, 不是授之以鱼而是授之以渔. 第9题的答案对于第2题没有用处, 第9题的“知其然”不能照搬到第2题, 第9题的“知其然”却可以拿去攻克第2题的难关. 两道题虽然有不同的答案, 不同的“然”, 却有共同的“所以然”. “知其然”只能回答1个题, 就好比一次性杯子, 用一次就没用了.“所以然”则是你喝水的嘴巴, 可以反复使用不断喝水维持生命. “所以然”不是为了对“然”锦上添花甚至无病呻吟,而是举一反三推而广之放之四海而皆准.
“然”就是具体,“所以然”是抽象. 抽象就是很多不同的具体事物的共同点. 数学抽象核心素养就是善于掌握不同数学问题的共同点, 将这个问题的解决方案用来攻克许许多多别的问题, 这就叫举一反三. 不仅是反三, 而且可以举一反万, 举一反无穷. 本套题通过提示第9题帮你解第2题, 让你解第11题得出一个公式拿去解第1题, 既是考察你举一反三的能力,也是帮助你提高这种能力. 也就是考察和培养你的数学抽象核心素养.
很多人写文章批判死记硬背. 死记硬背并不错, 总有些基本知识需要死记硬背. 问题在于, 死记硬背之后怎么用, 是只能用一次, 还是可以用多次? 是死用还是活用. 当然, 死记硬背还有一个毛病是效率太低, 只是像巴甫洛夫的狗那样通过反复重复来硬背, 如果能够让学生在理解的基础上记忆, 效率会提高. 但很多老师只会重复不会理解, 你也不能强求他提高效率. 哪怕他的效率低, 记住了也比没记住好. 写文章批评他, 他也不服气. 他的目的是应付考试. 只有用考试来教育他才有效. 教育不了老师, 那就教育学生, 总能够挽救几个.我出这套题就是希望用做数学题来教育考生. 哪怕考生都死记硬背, 我提示一下, 有些人醒悟了, 接受了提示举一反三了, 尝到了甜头, 以后他就会喜欢“所以然”. 喜欢只是一个开端, 不可能把什么道理都搞清楚,搞不清楚的就留在那里, 只知其然不知其所以然, 也比不知其然好. 只要他有这个愿望知其所以然, 这个愿望就能让他受益终身. 另外一些人不醒悟, 被淘汰, 如果失败能够使他有所醒悟, 也是我教育的效果.
如果一个考生没参加课外培训, 没有人告诉他椭圆面积公式, 不知道第9题的答案, 他也许会认真阅读思考一下我的提示, 按照提示做出第9题. 如果他的悟性再好一点, 有可能再按照这个提示做出第2题. 另外一些考生参加过培训, 知道椭圆面积公式, 马上就做出了第9题. 这本来是好事, 可惜他信奉“然”不信奉“所以然”, 为自己靠死记硬背做出了第9 题而沾沾自喜, 就再也做不出第2 题, 丢了那9分. 其实, 我的考试并不指望考生预先就知道椭圆面积公式的所以然, 那个所以然要用到定积分, 还需要变量代换, 中学生很难掌握. 我的提示是告诉你另外一个所以然, 让你从这个路口进去自己探索答案. 那些不信奉所以然的考生对这个入口根本不看, 就失去了第2题得分的机会. 而且也会失去第1、4题得分的机会, 因为那两题也同样是要靠提示做出来. 其他的题会不会做呢? 第9题也许他背过答案会做, 第11题(1)有现成解法也许会做, 两题目共送19分. 其它题目既没有现成方法, 也没有提示, 知其然派不上用场, 全都得靠“所以然”. 没有提示“所以然”的难度都不大, 但是为了考察你对所以然的理解是否清楚, 设了些陷阱. 死记硬背是要吃亏的. 让你吃亏不是要害你, 而是希望用一点苦口的良药来医你的病. 对大部分人可能没有疗效, 总有些人有疗效吧.
以下两种解法不是写给中学生看的, 而是给大学生以及上过大学的中学教师看的.



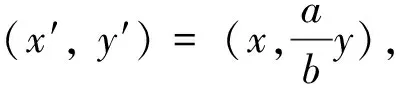
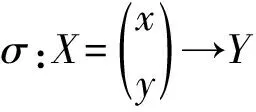

一般的考试中, 前几道题目都比较容易, 最后才会有几道难题. 我的考试前两道题就是杀威棒, 先让你束手无策. 考察你是否能够临危不乱, 处变不惊, 有耐心和平常心处理好下一道题. 下一个题是这样的:
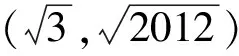
看起来, 这道题确实回归正常了. 虽然你只学过到两点距离之和为定值的点的轨迹是椭圆, 到定点和定直线距离相等的点的轨迹是抛物线. 像这样牛头对马嘴, 到定点和定直线距离之和为定值的点的轨迹没见过, 但总不像前两道题那样束手无策, 有办法按部就班列方程把它算出来:

图2
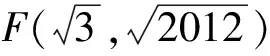
由题意列方程
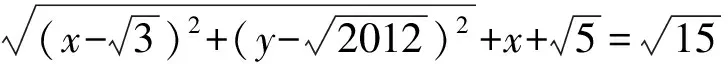
(1)

(2)

(3)
图象是抛物线的一段.
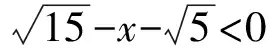

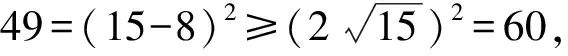
然而49<60, 这说明

本题答案: 空集.
防错能力本题解法按部就班, 答案却出乎意料. 设了一个陷阱,考察防错能力. 叫你求解, 就应该先考虑是否有解. 即使忘了考虑, 两边平方也应该立刻警惕是否增根.
考试时有的考生发现了无解, 就说题出错了. 无解也是解, 空集也是集合, 这是教材教过的. 空集也是轨迹, 也很正常. 如果题目真的出错了, 你举出理由指出错误, 也是正确答案. 高考不准指出错误, 我的考试准许, 我也希望高考用适当的方式准许指出错误. 考生能够看出错误, 就是优秀. 敢于指出错误, 是超级优秀. 高考说自己绝不会错, 所以不准指出. 你应该努力不出错误, 但也很难完全避免. 禁止指出, 就是禁止优秀.


4. 多项式(xsin 75°+sin 15°)2012被x2+1 除, 余式为________.
解此题看起来吓人. 其实不会当真要你求2012 次幂再求余式.
即使你没有学过多项式相除求余式, 但在小学算术中学过正整数a除以b求商q及余数r, 满足条件a=qb+r, 且0≤r f(x)=(xsin 75°+sin 15°)2012 =q(x)(x2+1)+(a+bx). 下一步怎么办? 你不可能算出2012次幂f(x)再作除法求余式. 既然只需要算余式a+bx不要求算商q(x), 只要在以上等式中取x=i使x2+1=i2+1=0, 就可将q(x) 消掉, 得到 (i sin 75°+ sin 15°)2012=a+bi, 算出前面的2012次幂, 就可得到a,b, 从而得到a+bx. 利用棣美弗公式(cosθ+isinθ)n=cosnθ+isinnθ可以算出 (i sin 75°+sin 15°)2012 =(cos 75°+ i sin 75°)2012 如果你不知道棣美弗公式, 就做不出本题. 不要紧, 先跳过去做后面的题. 做了填空题10就知道了. 10. 方程x3=-i 的全部解为________. (提示: 利用棣美弗公式(cosα+i sinα)n=cosnα+i sinnα. ) 不过, 你如果认为第10 题的提示只是用来做第10题, 而没有想到用来做第4 题, 第4 题的分就丢了. 丢的不是知识点的分, 而是核心素养的分, 因为你不会举一反三而丢了分. 1.几何模型:平面上的旋转 不论你是否学过棣美弗公式, 都必须明白这个公式的几何意义, 而不是把它作为代数计算公式来死记硬背. 也不需要学会用数学归纳法来证明这个公式. 如果你懂了数学归纳法, 也知道正弦余弦的和角公式, 自然就会用数学归纳法证明棣美弗公式, 不需要重新学习. 如果你还不会证明, 那也不用学, 不会就不会吧. 但有件事必须知道: i2为什么等于-1? 你觉得这个问题很奇怪: 书上规定的呀? 还需要问为什么吗? 书上规定了一个符号i 来表示-1的平方根. 并没有解释-1为什么存在平方根. 如果-1的平方根根本不存在, 怎么能够规定一个符号代表这个不存在的东西呢? 如果再问为什么(-1)2=1, 你觉得也是数学家规定的, 我们死记硬背, 应付考试就行了. 为什么(-1)2=1? 因为乘-1表示向后转. 比如汽车速度30表示每小时30 千米往东, 30乘-1变成-30, 就是向后转180°, 往东的30变成往西的30, 就是-30.-30再乘-1, 就是由往西的方向再次向后转, 回到往东的方向, 这解释了(-30)×(-1)=30. (-1)2表示后转两次, 转两个180°, 就是转360°, 还是回到往东. 既然-1 的平方是后转两次, -1 的平方根i 就是后转半次, 转半个180°, 也就是转90°. 这样, i2就是转两个90°, 转180°, 就是乘-1,这就解释了i2=-1. 转90° 有两个不同方向, 左转90° 与右转90°不一样. 我们规定左转(逆时针方向) 90° 为i, 右转90° 就是-i, 都是-1 的平方根: i2= (-i)2=-1. 往东30 乘i 变成30i 就是往北,再乘i变成30i2=-30 就是往西, 再乘i变成30i3=-30i 就是往南.30i4=30 回到往东. 既然i表示左转90°, 它的平方根就是左转45°, 就是 复数x+yi 代表向量(x,y). 要将(x,y) 左转(逆时针方向) 90°,只要用i乘x+yi 得到-y+xi, 就知道(x,y) 左转90°变到(-y,x). 要将(x,y) 旋转任意角α, 只要用cosα+ i sinα乘x+yi 得 (cosα+ i sinα)(x+yi) =(xcosα-ysinα)+i(xsinα+ycosα) 这表示: (x,y) 旋转角α变到(xcosα-ysinα,xsinα+ycosα). (cosα+ i sinα)n将旋转α的动作重复n次, 共旋转n. 因此 (cosα+ i sinα)n= cosnα+ i sinnα. 这叫做棣美弗公式.几何意义是: 每次旋转α, 重复n次旋转nα. 例1已知sinα; cosα, 求sinnα; cosnα. 解cosnα+ i sinnα=(cosα+ i sinα)n sin2k+1α+ … 例如cos 3α=cos3α-3 cosαsin2α =cos3α-3 cosα(1-cos2α) =4 cos3α-3 cosα, sin 3α=3 cos2αsinα-sin3α =3(1-sin2α) sinα-sin3α = 3 sinα-4 sin3α. 例2求方程xn=1 的全部复数根. 解设x=r(cosα+i sinα). 由xn=rn(cosnα+i sinnα)=1得 方程xn=1 的解就是1 的n次方根, 称为n次单位根. n次单位根在复平面上对应的n个点是圆心在原点的单位圆内接正n边形的n个顶点. 2.矩阵模型(仅供学过线性代数的中学生和中学教师看) 用复数a+bi作乘法将x+yi变到 (a+bi)(x+yi)=(ax-by)+(bx+ay)i. 所代表的平面向量X变到 这是线性变换, 用矩阵A乘X来实现. 因此, 复数a+bi可以用矩阵 =aI+bJ 3.规定服从逻辑 最后一次扩充, 由实数到复数, i2=-1 却不举例, 强行规定一个符号i代表-1的平方根, 不解释-1的平方根为什么存在. 0x+0x=(0+0)x=0x ⟹(0x+0x)+(-0x)=0x+(-0x) ⟹0x=0. 4.代数模型 我们在实数集合R之外构造一个新数x满足方程x2+1=0. 先看x与实数加减乘产生哪些新数, 这些新数怎样参加运算. x自乘产生所有的正整数次幂xk. 每个幂xk乘实数产生单项式akxk. 单项式相加产生多项式f(x)=a0+a1x+ …+anxn. 这就产生了所有的实系数多项式, 组成集合R[x]. 其中的多项式可以按多项式运算法则加减乘, 得到的结果仍然在R[x] 中, 不再产生更多的新数. 凭什么说多项式的字母x是R之外的“新数”?x是变量, 可以任意取值. 每个多项式f(x)=a0+a1x+…+anxn是自变量x与常数a0,a1,…,an经过加减乘算出的函数. 按这个观点,R[x] 不是数的集合, 而是x的实系数多项式函数的集合.R中的实数a0也是x的函数, 只不过它是常数, 只取一个固定值a0.R之外所有的多项式f(x)取值都不是常数, 都要变化, 不同于任何一个常数.R[x] 中不同的多项式两两之差都不是0, 都是不同的函数. 要将函数集合R[x] 变成数的集合, 就要对x取值. 比如令x=c,让x取常数值c. 每个多项式f(x) 也就取常数值f(c). 函数集合R[x] 就变成所有这些f(c) 组成的常数集合. 如果c是实数, 这就是让R[x] 中两个不同的多项式x,c取同一个常数值c.R中的常数没有变,R之外的变量全部变成R中的常数. 特别地, x=c⟹x-c=0⟹q(x)(x-c)=0 (∀q(x) ∈R[x]), 非零多项式x-c以及它所有的倍式q(x)(x-c) 全部变成常数0. 每个多项式f(x) 除以x-c有唯一的商q(x) 和余式r, 得到 f(x)=q(x)(x-c)+r ⟹f(c)=q(c)(c-c)+r=r. 可见f(x) 的取值f(c) 完全由f(x) 除以x-c的余式r决定. 由于除式x-c是一次, 余式r是常数, 也就是余数. 同一余式r的所有多项式f(x)取值f(c) 相同, 都等于余数r. 这个结论称为余数定理. 特别地,f(c)=0⟺r=0, 就是说:c满足多项式方程f(x)=0⟺f(x) 被x-c整除. 这称为因式定理. 令x取值c导致f(x) 的取值由f(x) 除以x-c的余式决定. 也可以令x2取值-1, 导致 x2+1=0⟹q(x)(x2+1)=0⟹ f(x)=q(x)(x2+1)+a+bx =q(x)0+a+bx=a+bx, f(x) 的取值由它除以x2+1的余式a+bx决定. 同一余式a+bx的所有多项式f(x) 组成一个集合, 称为模x2+1的同余类. 由于除式x2+1 是二次, 余式a+bx不见得是实常数, 而是不超过一次的实系数多项式, 将它看成一个“数”,a+bx所在同余类中所有的多项式都看成这个数的表达式, 其中的余式a+bx称为标准表达式. 不同的同余类表达不同的数. 当b=0, 余式a+bx=a是实数, 同余类{a+q(x)(x2+1) |q(x) ∈R[x]} 表示实数a. 当a=0,b=1, 余式a+bx=x, 表达的数是R之外的一个新数, 记作i.x所在的同余类{x+q(x)(x2+1) |q(x) ∈R[x]} 都表示i. 任意余数a+bx是x的任意实数倍bx与任意实数a之和,a+bx所表达的数就是x表达的i 的实数倍bi 与实数a之和a+bi.a+bx所在同余类{a+bx+q(x)(x2+1)|q(x) ∈R[x]} 中所有的多项式都是a+bi 的表达式. C={a+bi |a,b∈R} 就是R[x] 中全体多项式所表达的全体数的集合, 其中的数a+bi 称为复数. 每个复数a+bi 是a与bi 两部分之和: 前一部分a称为实部, 是实数; 后一部分bi 称为虚部, 是i 的实数倍. i 称为虚数单位, 当b≠0 时bi 称为纯虚数. 两个复数a+bi,c+di 进行加减乘运算, 只要将它们的表达式a+bx,c+dx作加减乘运算, 得到的表达式再除以x2+1 求余式得到标准表达式. 特别地, 要计算i2+1, 将i 的表达式x平方加1得到表达式x2+1, 再除以x2+1 得到余式0, 就是标准表达式, 因此i2+1=0.同理, i2的表达式x2=-1+(x2+1) 除以x2+1得余式-1, 因此i2=-1. 一般地, 进行复数的加减乘运算, 只需先将i看成多项式字母x,进行多项式运算, 再将i2=-1 代入, 相当于除以x2+1 求余式. 这样得到的复数集合C={a+bi |a,b∈R} 不但做加减乘运算通行无阻, 当除数c+di≠0 时做除法也通行无阻: 测试题第4题是已经建立了复数再将x=i 代入 (xsin 75°+sin 15°)2012 =q(x)(x2+1)+(a+bx), 利用复数运算求余式. 在这里是反过来利用余式构建复数使i2+1=0. 也许你会问: 假如另外选一个除式作同余类. 比如除以x2-2. 同样地得到余式a+bx, 同样地将x所代表的数记为i, 满足i2=2. 注: 以上讲的利用同余类构造“新数”的方法, 就是大学抽象代数课程中的数域的代数扩张.

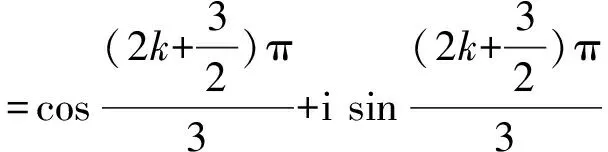
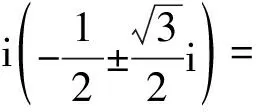

借题发挥: 什么是复数