φ-混合序列的随机中心极限定理

邢峰， 邹广玉

(长春工程学院 理学院, 吉林 长春 130012 )

1 引言及主要结果

定义1若

n→,

定义2若

Cov(f(X1,X2,…,Xn),g(X1,X2,…,Xn))≥0,

其中f和g是任何2个使上式协方差存在且对每个变元均单调非降的函数，则称随机序列{Xk,1≤k≤n}是相伴(associated)的. 如果对任何n≥2,{X1,X2,…,Xn} 都是相伴的，则随机序列{Xn,n≥1}是相伴的.

定义3定义随机变量X与Y之间的Kolmogorov距离为

IBRAGIMOV[2]给出了下列严平稳φ-混合序列的中心极限定理：

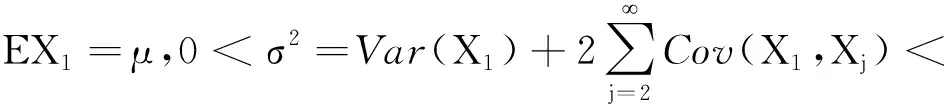
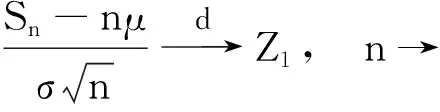
(1)

随机序列部分和的相关研究一直是概率极限理论研究的热点之一，它与很多实际问题密切相关，比如，保险公司在一定时间内的索赔可表示为随机部分和的形式，此外，金融数学、更新过程、证券、风险投资等领域中的问题也属于随机部分和问题. 因此，研究随机部分和的极限性质不仅具有理论意义, 更具有现实意义. 对此，很多学者已做了深入的研究[3-7].最近，PRAKASA等[8]在相伴情形下研究了随机中心极限定理，给出了与已有研究不同的结论.

首先给出一些假设条件和记号.

下文中总记{Xn,n≥1}为严平稳序列，且满足

{Nn,n≥1}为一列非负整数随机序列，且与{Xn,n≥1} 独立，假设

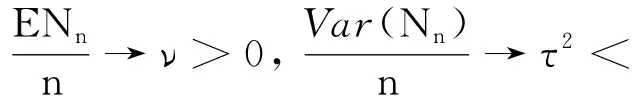
(2)

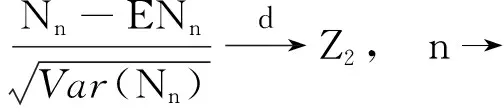
(3)

其中Z2为连续型随机变量. 记

定理B[8]设{Xn,n≥1}为严平稳的相伴序列,且{Xn,n≥1}, {Nn,n≥1}满足上述假设条件, 那么

dK(Tn,T(Z1,Z2))→0,n→.

目前对混合序列下的随机中心极限定理的研究还较少，本文研究φ-混合序列，得到

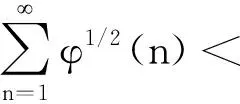
dK(Tn,T(Z1,Z2))→0,n→.

(4)

注1定理1说明在Kolmogorov距离下，适当正则化之后,随机部分和SNn依分布收敛于T(Z1,Z2),其中T(Z1,Z2)为2个独立随机变量Z1～N(0,1)和Z2的线性函数. 特别地，当Z2～N(0,1)时，T(Z1,Z2)～N(0,1).

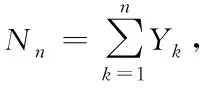
注3由定义可知,相伴序列和φ-混合序列互不包含,因此本文推广了已有的结果.

2 定理的证明

为了证明定理1, 需要以下几个引理.

引理1记P(Nn=k)=pn,k,cj=Cov(X1,X1+j),在定理的假设条件下，有

Var(SNn)=E(Nn)σ2+Var(Nn)μ2-

(5)

(6)

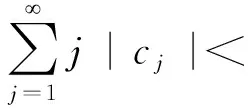
引理2[8]设{Un,U}为一随机变量序列，满足U的分布函数是α-Lipschitz连续的(α>0),V与{Un,U}独立的随机变量满足E|V|<.g为直线上的连续函数.那么对于任意的常数c，δ>0以及任意的z∈R，有

|P(Un+Vg(Un)≤z)-P(Un+cV≤z)|≤

P(|g(Un)-c|>δ)+2αδE|V|.

引理3[9]如果Fn⟹F,F在闭集A上处处连续,那么,

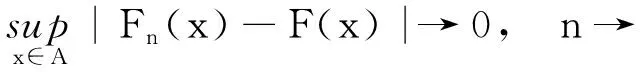
定理1的证明首先证明

dK(Tn,Tn(Z1))→0,n→.

(7)

记

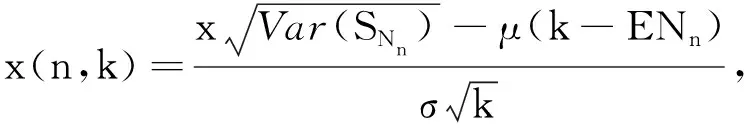
那么,由全概率公式以及{Xn}与{Nn} 的独立性,可知

P(Z1≤x(n,k))|+P(|Nn-nν|>nν/2)=∶

I1+I2，

由定理A和引理3，注意到标准正态分布函数的连续性，可知I1→0， 由Markov不等式以及式(2)，可知I2→0，从而得式(7)成立.

其次证明

dK(Tn(Z1),Tn(Z1))→0,n→.

(8)

由Chebyshev不等式以及式(2)和式(6)，易推得

(9)

由式(2)和引理1，可得

(10)

由式(10)以及Slutsky定理，知

(11)

注意到{Nn,Z2}与Z1独立，在引理2中取

由式(9)、(11)、引理3及δd的任意性，可推得式(8)成立.

接下来证明

dK(Tn(Z1),T(Z1,Z2))→0,n→.

(12)

注意到Z1与Z2独立,从而有

dK(Tn(Z1),T(Z1,Z2))=

P(T(u,Z2)≤x)|dΦ(u)=

其中,

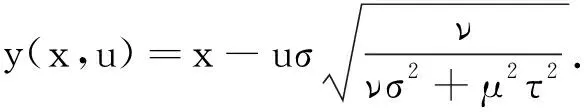
再由式(3)、引理3以及Z2为连续性随机变量，可知式(12)成立.

最后联立式(7)、(8)、(12)以及三角不等式：

dK(Tn,T(Z1,Z2))≤dK(Tn,Tn(Z1))+

dK(Tn(Z1),Tn(Z1))+dK(Tn(Z1),T(Z1,Z2)).

可知定理1成立.