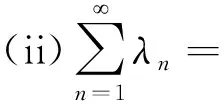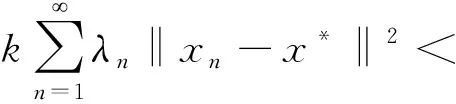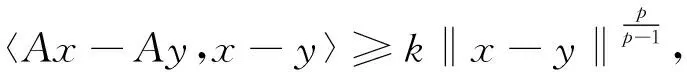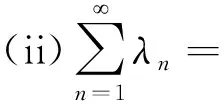Lp空间中Lipschitz强单调算子方程解的迭代算法

杨延涛

(延安大学 数学与计算机科学学院， 陕西 延安 716000)

单调算子的概念最早可追溯到对凸函数极值问题的研究.设Rn为n维欧式空间,f:Rn→R为正则的凸函数,f在x∈Rn处的次微分∂f(x)定义为

∂f(x)= {x*∈Rn:f(y)-f(x)≥〈y-x,x*〉,

∀y∈Rn}.

单调算子的概念与优化、变分不等式及均衡问题都密切相关,在非线性椭圆型、抛物型偏微分方程边值问题以及Hammerstein型非线性积分方程的可解研究中有广泛应用.

自从BROWDER等于20世纪60年代初引入单调算子的概念以来,经过50多年的发展,单调算子理论已相当成熟,成果颇丰. 1974年5月,美国数学会前主席BROWDER在美国数学会举办的“希尔伯特问题的数学结果”专题讨论会上提出了下述问题(OP)[1]:

设X是自反Banach空间,A:X→X*是连续、强制单调有界算子,A-1单值且有连续模,问: 是否能对方程Ax=0解的存在性给出一个构造性证明？此问题激发了国内外数学家的浓厚兴趣，并开展了广泛而深入的研究.

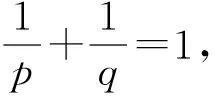
本文的目的是改进CHIDUME等[7]的广义最速下降法.使用新的分析技巧，以证明改进后的广义最速下降法依范数收敛于方程Ax=0的唯一解.

1 预备知识

设E是赋范空间,E*为E的对偶空间.定义映射J:E→2E*为

Jx={x*∈E*: 〈x,x*〉=‖x‖·‖x*‖,‖x‖=‖x*‖},

则称J为E上的正规对偶映像.

注1一般来说,J是一个多值映射.若E是光滑的,则J是单值的.

设E是光滑的实Banach空间,E*为其对偶空间.定义二元函数φ:E×E→R为

φ(x,y)=‖x‖2-2〈x,Jy〉+‖y‖2,x,y∈E，(1)

由式(1)及Cauchy-Schwarz不等式知

(‖x‖-‖y‖)2≤φ(x,y)≤

(‖x‖+‖y‖)2,x,y∈E，

(2)

由式(1)及正规对偶映像的定义可得

φ(x,y)=‖x‖2-‖y‖2-2〈x-y,Jy〉,x,y∈E.(3)

引理1设E为光滑的实Banach空间,{xn}与{yn}为E中的2个序列,其中之一为有界的.若xn-yn→0(n→),则φ(xn,yn)→0(n→).

证明不失一般性,假设{xn}是有界的,即存在正常数M,满足

‖xn‖≤M, ∀n≥1，

由于xn-yn→0(n→),故{xn-yn}也是有界的,即存在另一个正常数K,满足

‖xn-yn‖≤K, ∀n≥1，

利用范数的三角不等式可得

‖yn‖=‖yn-xn+xn‖≤‖xn-yn‖+‖xn‖≤

K+M, ∀n≥1，

因此{yn}是有界的.由式(3)可得

0≤φ(xn,yn)=‖xn‖2-‖yn‖2-2〈xn-yn,Jyn〉=

(‖xn‖+‖yn‖)(‖xn‖-‖yn‖)-2〈xn-yn,Jyn〉≤

(M+K+M)‖xn-yn‖+2(K+M)‖xn-yn‖=

(3K+4M)‖xn-yn‖,

由假设条件xn-yn→0(n→)得

φ(xn,yn)→0(n→).

推论1设E为光滑的实Banach空间,{xn}为E中序列,x∈E.若xn→x(n→),则

φ(x,xn)→0(n→).

在某些Banach空间中,引理1之逆也成立.

引理2[7]E=Lp(10，满足不等式:

‖J-1(u)-J-1(v)‖≤L1‖u-v‖,∀u,v∈Lq,(4)

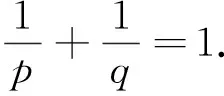
引理3[7]E=Lp(p≥2),则J-1在某个球上是Hölder连续的,即∀u,v∈Lq,满足‖u‖≤R,‖v‖≤R,有下列不等式成立:

(5)

其中，

定义1设X为实Banach空间,X*为其对偶空间,如果存在连续、严格增函数ψ:R→R,ψ(0)=0,使得

〈Tx-Ty,x-y〉≥ψ(‖x-y‖)‖x-y‖,

∀x,y∈D(T)，

(6)

则称算子T:X→X*为ψ-强单调的.

特别地,若ψ(t)=kt,k∈(0,1),则称相应的算子T为k-强单调算子.

定义2设Y为实Banach空间,Y*为其对偶空间,称算子A:D(A)⊂X→Y*在x0∈D(A)处半连续,若∀tn→0+,x0+tny∈D(A),y∈X,则有

引理4[7]设X为自反的Banach空间,T:X→X*为半连续ψ-强单调算子,则R(T)=X*.

推论2设A:Lp→Lq是Lipschitz连续的k-强单调算子,则方程Ax=0有唯一解.

证明在引理4中,取X=Lp,T=A,ψ=kt,则R(A)=Lq,特别地,方程Ax=0至少有1个唯一解x*∈Lp.设Ax=0还有另一个解y*∈Lp,由A的定义知

0=〈Ax*-Ay*,x*-y*〉≥k‖x*-y*‖2,

即可推出x*=y*,故方程Ax=0的解是唯一的.

引理5[8]设E是光滑的实一致凸Banach空间,{xn}与{yn}为E中的2个序列,其中之一是有界的.若φ(xn,yn)→0(n→),则

xn-yn→0(n→).

推论3设E是光滑的实一致凸Banach空间,{xn}为E中的一个序列,x∈E.若φ(x,xn)→0(n→),则xn→x(n→).

定义V:E×E*→R为

V(x,x*)=‖x‖2-2〈x,x*〉+‖x*‖2,

x∈E,x*∈E*.

(7)

比较式(1)和式(7) 可得

V(x,x*)=φ(x,J-1(x*)),x∈E,x*∈E*.(8)

引理6[9]设E是实自反、严格凸、光滑的Banach空间,则下列不等式成立:

V(x,x*)+2〈J-1x*-x,y*〉≤

V(x,x*+y*),x∈E,x*,y*∈E*.

(9)

2 主要结果

定理1设E=Lp(1

(10)

其中{λn}满足条件:

(i)λn→0(n→)，

则由式(10)所产生的序列{xn}强收敛于方程Ax=0的唯一解.

证明由推论2知，方程Ax=0有唯一解,记为x*.结合式(8)与式 (10)得

φ(x*,xn+1)=φ(x*,J-1(Jxn-λnAxn)) =

V(x*,Jxn-λnAxn),

(11)

结合式(9)与式(11) 得

φ(x*,xn+1)=V(x*,Jxn-λnAxn)≤

V(x*,Jxn)-2λn〈J-1(Jxn-λnAxn)-x*,Axn-Ax*〉=

φ(x*,xn)-2λn〈xn-x*,Axn-Ax*〉+

2λn〈xn-x*,Axn-Ax*〉-

2λn〈J-1(Jxn-λnAxn)-x*,Axn-Ax*〉=

φ(x*,xn)-2λn〈xn-x*,Axn-Ax*〉-

2λn〈J-1(Jxn-λnAxn)-J-1(Jxn),Axn-Ax*〉，

(12)

由J-1和A的Lipschitz连续性以及A的k-强单调性得

φ(x*,xn+1)≤φ(x*,xn)-2kλn‖xn-x*‖2+

2λn‖J-1(Jxn-λnAxn)-J-1(Jxn)‖‖Axn-Ax*‖≤

(13)

其中L1与L分别为J-1与A的Lipschitz常数.

由条件(i),选取n充分大,使得

φ(x*,xn+1)≤φ(x*,xn)-kλn‖xn-x*‖2，

(14)

从而有

kλn‖xn-x*‖2≤φ(x*,xn)-φ(x*,xn+1)，(15)

(16)

结合式(16)与条件(ii)，得

(17)

故存在一个子列{xnj}⊂xn,使得

xnj→x*(j→)，

由推论1得

φ(x*,xnj)→0(j→)，

因此

φ(x*,xn)→0(n→).

再由推论3得

xn→x*,n→.

定理2设E=Lp(2

设{xn}由下列方程产生:

(19)

其中{λn}满足条件:

(i)λn→0(n→),

则由式(19)所产生的序列{xn}强收敛于方程Ax=0的唯一解.

〈Ax-Ay,x-y〉≥ψ(‖x-y‖)‖x-y‖,∀x,y∈E.

因此A:E→E*为L-Lipschitz连续的ψ-强单调算子.由引理4知,R(A)=E*.

特别地,方程Ax=0至少有1个解x*∈E.

假设方程Ax=0还有另一个解y*∈E,则由式(18)得

即x*=y*,因此方程Ax=0在E中有唯一解,记为x*.

下证{xn}是有界的.

选取充分大的r>0,使得φ(x*,x1)≤r.假设φ(x*,xn)≤r,n≥1.现证φ(x*,xn+1)≤r,n≥1.

由式(5)、(9)、(18)和(19)以及A的L-Lipschitz连续性，有

φ(x*,xn+1)=φ(x*,J-1(Jxn-λnAxn))=

V(x*,Jxn-λnAxn)≤

V(x*,Jxn)-2〈J-1(Jxn-λnAxn)-x*,λnAxn〉=

V(x*,Jxn)-2λn〈xn-x*,Axn-Ax*〉+

2λn〈J-1(Jxn-λAxn)-J-1(Jxn),Axn-Ax*〉≤

φ(x*,xn)-2λn〈xn-x*,Axn-Ax*〉+

2λn‖J-1(Jxn-λnAxn)-J-1(Jxn)‖‖Axn-Ax*‖≤

(20)

由定理2的条件(i),令n足够大,使得

(21)

将式(21)代入式(20)，得

后续推导与定理1类似, 故从略.证毕!

注2定理1和定理2分别改进了文献[7]中的相关结果.特别需要指出的是，定理2去掉了文献[7]中对A-1(0)≠∅的假设.