逻辑函数高阶布尔e偏导数求解算法的实现
罗文强,王伦耀,夏银水
(宁波大学 信息科学与工程学院, 浙江 宁波 315211)
布尔导数和e导数能反映布尔函数值随变量变化的关系,二者被广泛应用于图像处理[1]、逻辑电路的故障检测[2-5]和布尔函数密码学性质的研究[6-9].
目前,学者对布尔e导数求解方法的研究主要有3种: 基于K图和降维K图的图形法[10]、基于最小项的表格法[11]和基于改进D图的算法[12].利用K图和降维K图求解布尔e导数,具有计算方法简单、物理意义清晰的特点,但随着输入变量数n的增大,其图形规模将以2n的速度迅速增加,因此此方法对输入变量超过30的大逻辑函数不适用;同样,通过列布尔1值最小项表求解布尔e导数,其最小项数量与输入变量数n成2n关系,亦不适合处理大函数;而基于改进D图求解布尔e导数的方法,其图形规模不仅与输入变量数n成an(1 布尔e偏导数[13]的求解较布尔e导数更难.文献[11]提出了一种基于最小项表求解布尔e偏导数的方法,即根据待求导变量累次列布尔1值最小项求解布尔e偏导数,其与基于最小项的布尔e导数求解方法一样,亦不适合求解大函数的布尔e偏导数. 本文给出了一种便于计算机编程实现的逻辑函数高阶布尔e导数和e偏导数的求解算法.利用乘积项集合之间的不相交操作[14],实现逻辑函数的逻辑“与”操作,并结合布尔e导数和e偏导数的定义,给出了求解算法.采用二级逻辑综合工具espresso,对算法的最终输出结果进行简化,进而得到更加紧凑的求导结果. 一个n变量布尔函数f(x1~xn)总可以写成式(1)所示的乘积项之和(sum of product, SOP): (1) 式(1)中pi为布尔函数f的第i个乘积项,k为乘积项的个数,符号“∑”表示乘积项之间是逻辑“或”关系,并记f的乘积项集合为Cf.若乘积项pi∈Cf,则pi可写成: (2) 例如,乘积项p=x1x2x3=-1-,按上述约定可将变量x1,x3全取“-”,写成DC(x1,x3);变量x1,x2,x3不全取“-”写成EN(x1,x2,x3). 定义1设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj(1≤j≤n)的一阶布尔e导数为 (3) 定义2设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj1~xjk(2≤k≤n)的k阶布尔e导数可表示为 (4) 推论1设n变量布尔函数f对应的乘积项集合Cf由(s+t)个不相交乘积项构成,即pi·pj=∅ (i≠j),其中,s个乘积项中的待求导变量均不出现,而另外t个乘积项中的每个乘积项至少有1个待求导变量出现,则k(1≤k≤n)阶布尔e导数可表示为 证明将构成逻辑函数f的(s+t)个不相交乘积项拆分成g和h两部分,且f=g+h.其中,g中包含s个不相交乘积项,且任一乘积项中的待求导变量均未出现;h中包含t个不相交乘积项,显然属于h的任一乘积项中的待求导变量至少出现1个.因此,g和h可以表示为 由条件pi·pj=∅(i≠j)可知g·h=∅,故 证毕! 解由推论1可得 由定义2及计算可得 以上2种方法的计算结果是一致的.用推论1来实现布尔e导数,其求导过程中逻辑表达式之间的逻辑“与”操作更加简单. 定义3设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj(1≤j≤n)的一阶布尔e偏导数为一阶布尔e导数. 定义4设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj1~xjk(2≤k≤n)的k阶布尔e偏导数可表示为 (6) 推论2设n变量布尔函数f对应乘积项集合Cf由pi·pj=∅(i≠j)个不相交乘积项构成,即pi·pj=∅(i≠j),其中s个乘积项中的待求偏导变量均不出现,而另外t个乘积项中每项至少有1个待求偏导变量,则k(1≤k≤n)阶布尔e偏导数可表示为 (7) 式(7)中,h为布尔函数f的子函数, 证明用数学归纳法: (1) 当阶数k=1时,由定义3知,利用推论1可证明式(7)成立,即 (2) 假设当阶数k=q(1 由步骤(1)~(3)可知,对任意阶数k(1≤k≤n),推论2成立. 证毕! 由布尔e导数和e偏导数的定义可知,逻辑函数的布尔e导数和e偏导数的求解过程中都涉及求解函数之间的“与”运算.因此,求解逻辑函数的逻辑“与”直接影响布尔e导数的求解速度和规模.下文将讨论逻辑函数之间“与”运算的求解方法以及大函数高阶布尔e导数和e偏导数算法.考虑现有的布尔e导数和e偏导数的求解方法只适用于输入变量较少的逻辑函数的低阶求导,且对求导结果未进行逻辑简化,本文将借用已有的二级逻辑综合工具espresso,对布尔e导数及e偏导数的计算结果进行逻辑简化. 定义5若Cf和Cg分别为逻辑函数f和g所对应的乘积项集合,则Cf与Cg之间的不相交运算用Cf⊗Cg表示,且Cf⊗Cg=Cf-Cf∩Cg,符号“⊗”为2个逻辑函数之间的不相交运算符. 从定义5可以看出,Cf⊗Cg的实质是在Cf中除去与Cg相交的部分,因此,Cf⊗Cg的结果属于Cf且不与Cg相交的部分;由此可得:Cf与Cg相交部分等于在Cf中除去与Cg不相交的部分,即逻辑函数f和g“与”的结果可表示为 Cf∩Cg=Cf⊗(Cf⊗Cg). (8) 算法伪代码如下: 图1中,Cf和Cg分别包含w和v个乘积项,Cdis=piΘqj表示乘积项pi与qj之间进行不相交锐积运算,运算结果寄存在Cdis中.显然,结合图1算法和式(8)可实现逻辑函数f和g之间的逻辑“与”运算. 本文中,k阶布尔e导数运算用程序E_Derivative(Cf,L)来实现,其中Cf是布尔函数f转化为不相交乘积项SOP形式的乘积项集合,L是一个链表,用来寄存待求导变量,其伪代码如下: 图2中,Cen和Cr_en为2个乘积项集合缓存,CT是运算结果;子函数Apart(Cf,L)的功能是根据链表L中寄存的待求导变量出现的情况将Cf中的乘积项拆分成两部分,其中集合Cdc中寄存待求导变量均不出现的乘积项,剩余部分寄存在集合Cen中;子函数Reverse(Cen,L)的功能是将Cen中在全部乘积项中出现的待求导变量取反;Cand=Cen⊗(Cen⊗Cr_en)实现了Cen∩Cr_en功能,即实现2个逻辑函数之间的逻辑“与”运算;最后,借用espresso工具对CT进行逻辑简化,得到更加紧凑的逻辑表达形式. 本文k阶布尔e偏导数运算可用程序E_PartialDerivative(Cf,L)来实现,其中Apart(Cf,L)的含义同图2,其伪代码如下: 图3中的Cen是乘积项集合缓存,CT是运算结果;Cpar=e_Derivative(Cen,Lxi)表示对链表Lxi中的唯一待求偏导变量xi求一阶布尔e导数,即一阶布尔e偏导数;最后,借用espresso对CT实现逻辑简化. 之后求Cen∩Cr_en,即 本文给出的逻辑函数高阶布尔e导数和e偏导数的求解算法已经在Windows10/CPU 2.40 GHz/ RAM 8.00 GB/VS2010环境下使用C语言编程实现,并利用MCNC标准测试电路进行了实验验证. 表1给出的是k阶布尔e导数和e偏导数的实验数据.表1中的电路f取自MCNC标准测试电路;i/o/p分别表示电路f对应的输入变量、输出变量和乘积项的数量;阶数k表示对电路f的任意k个变量求解布尔e导数和e偏导数,1≤k≤n,n为变量数;Cd表示布尔e导数计算结果经espresso逻辑简化后的乘积项数量;Cp表示布尔e偏导数计算结果经espresso逻辑简化后的乘积项数量;td表示布尔e导数的求解时间,单位ms;tp表示布尔e偏导数的求解时间,单位ms;“<1”表示求解时间小于1 ms. 表1给出了11组MCNC测试电路的实验数据,这些电路的变量数为7~199,其输出和乘积项数均具有一定的规模;每个电路均测试了3组不同阶数k的情况.从表1中可以明显看出,算法处理时间较短,大部分都<1 ms,无超过1 s的. 如果用|Cd|和|Cp|分别表示Cd和Cp中所包含的乘积项数量,从表1可以看出,一般情况下|Cd|≥|CP|,其原因除了与espresso逻辑优化有关外,还与它们的定义有关.对于逻辑函数f的k阶布尔e导数而言,是2个逻辑函数之间的“与”运算;但对于k阶布尔e偏导数,则是2k个逻辑函数之间的“与”运算;一般情况下,2k个逻辑函数之间的公共部分更少, 表1 布尔e导数和e偏导数的实验数据 即多次“与”运算后对应的乘积项数量更少,导致|Cd|≥|Cp|. 函数间不相交运算的速度与每个函数包含的乘积项数量有关,待处理的逻辑函数的输入变量数对其不敏感.有些函数适合拆分,拆分后实际参与不相交运算的乘积项数量不多,因此速度快.例如电路i7、xparc.本文中逻辑函数的布尔e导数用不相交运算来求解,显然不相交运算的调用次数将直接影响算法的速度.对于逻辑函数f的k阶布尔e导数而言,由式(8)知,需要2次不相交运算,但k阶布尔e偏导数却需要2k次不相交运算,因此有tp≥td. 实现大函数的布尔e导数和e偏导数的求解主要由以下两部分构成: (1)用逻辑函数之间的不相交运算替代.待处理的逻辑函数的输入变量数对不相交运算的速度不敏感,故在处理大逻辑函数时效率较高;(2)在求导过程中,将函数拆分成两部分,即不包含待求导变量的乘积项集合Cdc和包含待求导变量的乘积项集合Cen.Cdc求布尔e导数的结果是其本身,因此,实际上只有Cen参与了求导过程中的不相交运算,显然Cen中包含的乘积项数量不会大于原函数,从而达到减少参与不相交运算的乘积项数量的目的,提高了算法速度.实验表明,本文提出的方法可以快速计算输入变量数在199内的大函数的高阶布尔e导数和e偏导数.为了简化求导后的逻辑函数的表达式,算法最后借用二级逻辑综合工具espresso,实现了函数的逻辑简化.1 定 义
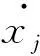
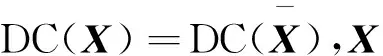

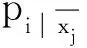



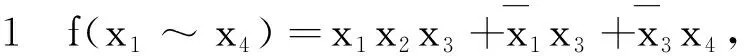
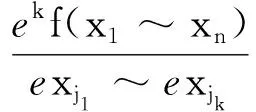


2 算法实现
2.1 逻辑函数之间逻辑“与”运算的实现

2.2 k阶布尔e导数算法的实现
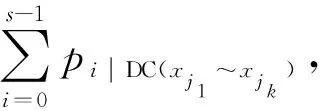

2.3 k阶布尔e偏导数算法的实现
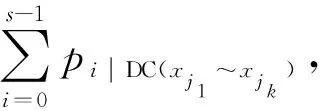


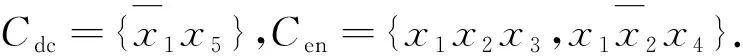
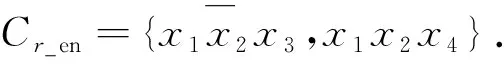
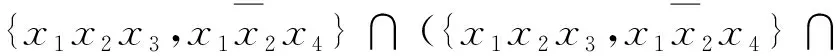

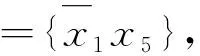
3 实验结果与分析

4 结 论


