临界半线性波动方程解的有限时间破裂
汪海航,蒋红标
(1. 浙江理工大学 理学院, 浙江 杭州 310018; 2. 丽水学院 工学院, 浙江 丽水 323000)
0 引 言

(1)
其中初值满足
(2)
且p=pc(n),pc(n)为二次代数方程:
的正根,即
该问题为以下半线性波动方程小初值Cauchy问题(Strauss猜测)的拓展:
(3)
其中,n≥2,ε>0为小参数.已知结果表明,问题(3)存在一个临界指数p0(n),为下述二次方程的正根:
临界指标是指正实数p0(n)将(1,+)分成(1,p0(n)]和(p0(n),+)2个区间.当p∈(1,p0(n)]时,问题(3)不存在整体解;当p∈(p0(n),+)时,问题(3)对小初值有整体解.

此后,一些学者研究了问题(3)在外区域上的初边值问题,得到次临界情形、临界情形的若干破裂结果、生命跨度估计及超临界情形的整体存在性结果,相关进展可参考文献[15-20].
最近,李卓然[21]研究了带次临界指标(1 本文主要研究带临界指标p=pc(n)的Cauchy问题(1),证明了解将会在有限时间内破裂,主要结果如下: 定理1设n≥5,且初值f与g满足式(2).假设问题(1)有解 (u,ut)∈C([0,T),H1(Rn)×L2(Rn)), 使得 supp (u,ut)⊂{(x,t): |x|≤t+R}. 文中,记号C表示常数,在不同的地方可表示不同的值. 为证明本文的主要结论,需要应用以下引理: 引理1[9]设p>1,a≥1,且(p-1)a=q-2.t≥T0>0,若F∈C2([0,T))满足 F(t)≥K0(t+R)a, (4) 且 F″(t)≥K1(t+R)-q[F(t)]p, (5) 其中K0,K1,T0和R是正常数.当固定K1,存在C0>0且C0不依赖于T0和R,使得K0≥C0,则T<,即F(t)在有限时间内破裂. 为了叙述引理2,参照文献[9]引入试验函数: (6) 且定义函数 ψ1(x,t)=φ1(x)e-t. (7) 现引入2个泛函: (8) 其中ψ1(x,t)为由式(7)定义的函数,u为问题(1)的解.u所满足的假设条件蕴含了F0(t)与F1(t)关于t连续可微. (9) 引理3[21]设p>1,则 (10) 为了得到临界情形的破裂结果,采用文献[9]的方法建立一个关于非线性项的改进的下界估计.不失一般性,假设u(·,t)为径向函数.否则可定义 由达布公式可知: 其中,ω∈Rn为单位向量[22].引入u关于空间变量的Radon变换: (11) 其中,dSx为在超平面{x|x·ω=ρ}上的Lebesgue测度,容易证明R(u)仅依赖于ρ和t,而与ω无关.由式(11)和径向对称条件可得 令 (12) 这意味着R(u)(ρ,t)不依赖于ω. 由于u是问题(1)的解,显然R(u)满足一维波动方程: R(|u|p(1+|·|2)α)(ρ,t), (13) 由D’Alembert公式和假设条件:u的初始值是非负的,可得 R(u)(ρ,t)≥ (14) 注意到suppu(·,s)包含于半径为s+R、圆心为原点的球B(0,s+R)内,若|ρ1|>s+R,由于向量y垂直于单位向量ω,则可得 因此 R(|u|p(1+|·|2)α)(ρ1,s)= 即 suppR(|u|p)(·,s)⊂B(0,s+R). (15) 由式(14)和(15),得到 (16) 由式(10)可得 结合式(16)及ρ≥0,得到 (17) 下面引入函数f∈Lp(R)的一个变换: (18) 注意到 其中M(|f|)为f的极大值函数.因此,存在C>0, ‖T(f)‖p≤C‖f‖p, (19) 令 则有 (20) 当r≥ρ且1 (21) (22) 由式(12)且注意到suppu(·,t)⊂B(0,t+R),可得 (23) 结合式(21)与(23),有 (24) 由式(17)R(|u|)的下界,并结合式(24)及r≥ρ,得到 当ρ∈(0,t-R-1)时,显然存在常数Cn>0,对所有t>2(R+1),有 (t-ρ+R)≤Cn(t-ρ-R), 由此可得 (25) 由于p是满足式(1)的临界指数,即 (n-1)p2-(n+4α+1)p-2=0, 从而有 由式(25), (26) 由此, 根据上式,重新定义下界 C(t-R)n-1-(n-1)p/2+2αln(t-R-1-(t-R-1)/2)≥ C(t-R)n-1-(n-1)p/2+2αln(t-R)/2, 结合式(1)与式(8),有 C(t-R)n-1-(n-1)p/2+2αln(t-R)/2, (27) 可知,式(27)的下界较式(10)的下界多了一项lnt. 由于n-1-(n-1)p/2+2α≥0,当n≥4时,对式(27)积分2次,得到 F0(t)≥C(t-R)n+1-(n-1)p/2+2αlnt, 有 由于t充分大,显然 因此 F0(t)≥K0(t+R)n+1-(n-1)p/2+2α. (28) 其中当t充分大时,K0>0为任意大数.结合式(9)与(28),在引理1中取参数 a=n+1-(n-1)p/2+2α, 即得对满足条件(p-1)[n+1-(n-1)p/2+2α]=n(p-1)-2α-2且p>1的p有p=pc,定理1成立.当p=pc(n)且初始条件满足式(2)时,问题(1)的解在有限时间内破裂. 由式(22)中的条件可知α>0.下面验证 (29) 由pc(n)的表达式可知,式(29)等价于 即验证了式(29). 另一方面,式(21)中要求1 即 3n-(4α+5), 亦即 综合可得
1 预备知识
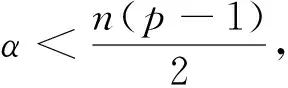
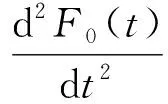
2 定理的证明
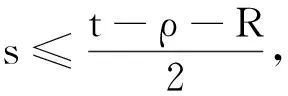
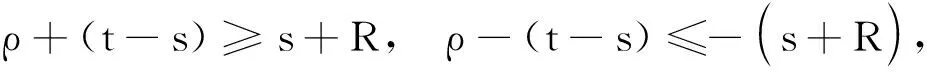
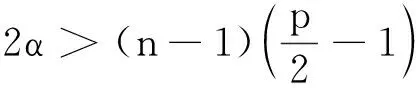
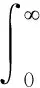
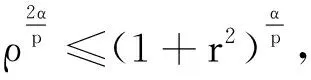
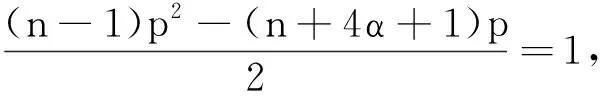

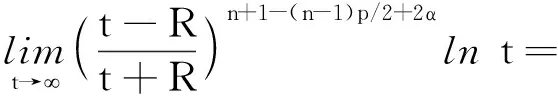
q=n(p-1)-2α,3 α的取值范围



