关于数形结合的几点思考
邢志远
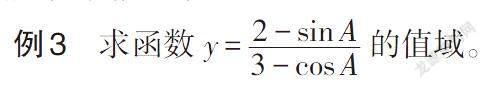
摘 要:数形结合是一种重要的数学思想,在高中数学教学中有重要的作用。对于学生数形结合能力的培养,教师应该从基础做起,从简单做起,让学生认识到数形结合在学习中的作用和效果,在“数”的基础上逐渐建立起“形”的意识。
关键词:高中数学;数形结合;转变思维
在数学学习过程中,学生从数学运算到函数研究,接触到函数图象,再从数学的理论概念到平面,以及空间图形的理解与掌握,看似互不相关,实则密不可分。“数”是数学中的理论基础,而“形”则是与数相辅相成的模型构建,只有处理好数与形的关系,才能更好地去理解和掌握数学知识。
一、重视基本概念,理解基础图象
这里所说的“形”其实就是学习中的各种函数图象、几何图形等。在解答数学题时,如果已知条件只是单独给出了数据或是图形,那么为了快速、有效地解决问题,我们还需要拿出一部分精力对图形进行专门的学习和研究,只有理解、掌握了基础图象及其变化规律,才能更好地将“数”和“形”有机结合起来,巧妙运用。因此,高中数学教学要求教师要重视对基础概念和基础图象知识的培养,这样对学生准确解读题目的含义、把握解题思路、做出正确解答有很大幫助。数学教师要把向学生渗透数形结合的思想方法作为日常教学任务,培养学生形成数形结合的思考逻辑和解题思维,进而提高教学效率。
二、运用数形模型,处理变化关系
学生一直将对函数性质的理解视为一大难题。究其原因,主要是因为这方面的知识内容比较抽象,学生理解起来有一定的难度。为了消除此种不利的教学现象,教师可以将数形结合的教学理念引入到教学中,借助对函数图象的理解和强化,帮助学生理解知识,鼓励学生使用函数图象来处理相关数学问题。
例1 已知方程x2 - 4x + 3 = m有4个根,求实数m的取值范围。
求方程根的个数问题可以转化为求两条曲线的交点的个数问题来解决,即求解函数y = x2 - 4x + 3与函数y = m图象交点的个数。如此一来,原本抽象的数量变化关系就变得十分具体。
三、建立“形”的概念,形成思维转变
笔者根据教学经验得出,如果把教学重点全部放到对基础概念的理解上,或者把学生成绩的提高寄托在大量做题上,并不是促进学生成长的正确途径,而有目的地训练学生思维的发散性,让学生多角度、多方位地去思考和质疑,对学生的持续性发展还是有很大帮助的。在经过小学和初中的学习后,很多学生已经形成了一种用理论性的思维处理问题的思维定势,教师要有目的性地激励、引导学生从图形和图象入手,逐步建立“形”的概念,让学生意识到“形”在解决问题中的作用。这个过程实现的实质就是思维模式的转变,学生要从原有的思维框架中跳出来,从“形”的角度建立起与数学理论概念相对应的一种理解和解决问题的方法。因此,教师要在日常教学活动中要有目的地训练学生的思维,能够使学生转变思维的情境和氛围,促进学生思维方式的良性循环。
四、提升分析能力,培养应用意识
数形结合贯穿于高中数学学习的整个过程中,在很多简单的概念和习题中都有所体现,不是只有难题才会运用到。这就要求学生要从日常学习的点点滴滴入手,把数形结合作为学习的一种有效工具,进而形成一种思维方式,用一个崭新的视角来分析和处理问题。
例2 若集合A,B,C满足[A∪B∪C=1,2,][3,…,10,] 求满足条件的集合的有序三元组[A,B,C]的个数。
A,B,C三个集合如果用韦恩图画出来,最多可以分成七个部分。也就是说,要把这10个数放到这七个部分中,类似抽屉原理。利用韦恩图这个问题可以轻松求解,但是如果用分类列举的方式求解,就会费时费力,事倍功半。
例3 求函数[y=2-sinA3-cosA]的值域。
此题变形后可以用“提斜边”的方法来解决,这是学生最容易想到的方法,但是此种方法计算量大,也容易出错。其实,学生可以用构造斜率的方式来解决问题,即[2,3]和[sinA,cosA]为两点的坐标,此题即变为求这两点构成的直线的斜率的取值范围,这样问题就变得简单明了了。
实践表明,在教学基本概念和基本公式时,教师应该通过各种各样的方式和途径把抽象的数学概念直观化,使学生易于理解。基于此,教师在教学时要多动脑筋,多从学生的角度思考问题,利用多媒体技术将数学知识以更加丰富多彩的形式呈现给学生,活跃课堂教学氛围,激发学生的学习兴趣,加深学生对数学知识的理解。多媒体教学对于培养学生创新能力有着很大的帮助,教师要在数学教学中妥善运用,使学生真正领悟数形结合给学习带来的便利。
参考文献:
[1]夏炳文. 关于数形结合的一点思考[J]. 高中数学教与学,2016(13).

