基于下侧H-平均距离的风险度量

黄薏舟

（新疆财经大学 金融学院，乌鲁木齐 830012）

0 引言

近几十年来学者们对金融风险及其度量的研究逐步展开。Markowitz（1951）[1]提出了用方差作为风险度量的思想，但是该度量方法提出不久就受到许多质疑，为此他又提出了用半方差度量风险的思想。Konno和Yamazaki[2]则提出可以用投资收益的绝对离差度量风险的想法，并在此基础上建立了他的投资组合模型。Yamazaki[3]则将Gini系数作为风险度量，并建立了均值-Gini模型。自Roy[4]提出用收益小于某个参照值的概率度量风险的想法后，对下侧风险度量的讨论渐渐多了起来。Bawa[5]提出了用下偏矩度量风险的想法，Fishburn[6]则提出了(α，t)作为风险度量的思想。以外，被提出的风险度量方法还有损失期望值、绝对半离差、β系数、在值风险、ES(Expected shortfall)、WCE等。

除了对风险度量方法的研究外，风险度量方法与随机占优的一致性也是学者们的一个重要的研究内容。Porter[7]就证明了用关于某固定目标收益的半方差作为风险度量时，所导出的均值-风险模型与随机占优是一致的。Yit⁃zhaki[3]证明了用Gini系数度量风险时均值-风险模型与二级随机占优是一致的。Ogryczak和Ruszczynski[8]证明了半标准差作为风险度量时均值-风险模型与二阶随机占优是一致的，同样的结论适用于绝对半偏差。Gotoh和Konno[9]将结果推广到了三阶随机占优。Ogryczak和Ruszczynski[10]将上述结论进一步的推广，证明了若以低于均值的k阶中心半偏差作为风险度量，则均值-风险模型与二阶随机占优是一致的。

本文提出了一种新的风险度量方法并讨论了该方法的性质。研究发现，该风险度量方法不仅涵盖了一些常用的风险度量方法，而且与一级、二级随机占优是一致的。因此，该风险度量方法具有一定的研究价值。

1 基于下侧H-平均距离的风险度量

设X表示某种投资的随机收益，Markowitz给出的风险度量为：

Yamazaki[3]提出了用Gini系数度量风险的思想，并讨论了均值-Gini系数分析方法与二级随机占优的一致性问题。设X表示投资的随机收益，Gini系数被定义为：

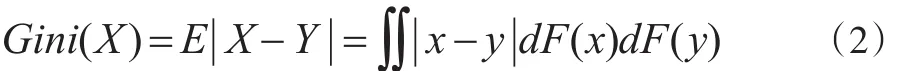
其中，Y是与X独立同分布的随机变量，F(x)为随机变量X的分布函数。

从数学上看，方差度量的是随机变量偏离其均值的程度，而Gini系数实际上就是随机变量X到自身的距离。似乎方差和Gini系数没有什么联系，但给出方差的另一个定义，就会发现他们之间的联系。方差还可以被定义为：

其中，Y是与X独立同分布的随机变量，F(x)为随机变量X的分布函数。可以证明：方差和Gini系数都满足非负性、对称性和三角不等式，都可以用来描述随机变量到自身的距离。

下面给出包含上述两种距离的更为一般的H-平均距离的概念。

定义1：设X是与Y独立同分布的随机变量，H(x)为非负的凸函数，当x＞0时H(x)为单调递增函数，当x＜0时H(x)为单调递减函数，且满足H(0)=0。称E(H(X-Y))为随机变量X到自身的H-平均距离。

可以证明：H-平均距离满足非负性、对称性和三角不等式三条公理。若F(x)为随机变量X的分布函数，则随机变量X到自身的H-平均距离为：

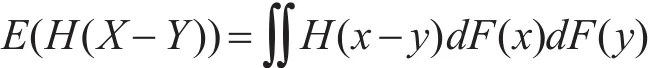
特别地，当H(x)=|x|时，H-平均距离即为Gini系数，当时，H-平均距离即为方差。可见，H-平均距离是上述两种随机变量到自身距离的推广。

方差与Gini系数都可以用来度量风险，同样，H-平均距离也可以用来度量风险。为此，构造如下形式的风险度量：

式（4）定义的风险度量虽然包括诸如方差、Gini系数等风险度量方法，但它也存在不足之处。一是方差就包含在该风险度量方法里，而均值-方差分析方法与二级随机占优是不一致的，说明直接用于ρ1(X)=E(H(X-Y))度量风险与随机占优之间存在不一致性。二是该风险度量不属于下侧风险范畴。根据Koszegi等[11]的思想构造X的风险度量：

其中H(x)为一定义在R+上的单调递增的非负凸函数且满足H(0)=0，Y是与X独立同分布的随机变量，(X-Y)+=max(X-Y，0)。

若F(x)为随机变量X的分布函数，Y为与X独立同分布的随机变量，X的概率密度函数为f(x)，则X的风险度量为：

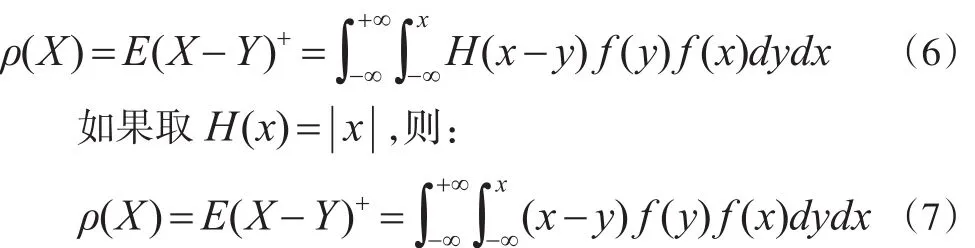
注意此风险度量与Gini系数不同。Gini系数是随机变量X与自身的距离，而该值是随机变量X与自身的下侧距离，它明显要比Gini系数小，称之为下侧Gini系数。

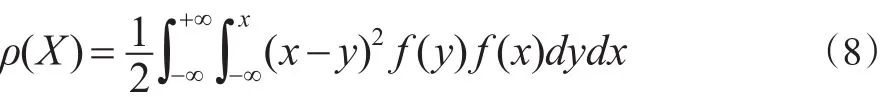
一般来讲，此风险度量与方差也不同，它要比方差来的小。不妨称之为下侧方差。

2 风险度量的性质

要讨论风险度量的性质，不得不说风险度量所满足的公理。1999年，Artzner[12]等首次提出风险度量所满足的四条公理，即平移不变性、正齐次性、次可加性、单调性公理。

公理1（平移不变性公理）：对于任意实数C，风险度量ρ(X)满足ρ(X+C)=ρ(X)-C。

公理2（正齐次性公理）：对于任意正数λ，ρ(X)满足ρ(λX)=λρ(X)。

公理3（次可加性公理）：对于任意随机收益X，Y，ρ(X)满足ρ(X+Y)≤ρ(X)+ρ(Y)。

公理4（单调性公理）：对于任意随机收益X，Y，如果它们满足X≤Y，则ρ(X)≥ρ(Y)。

Pflug[13]认为一致性风险度量公理的前三条具有一定的合理性，但单调性公理需要进行修改。他将单调性公理改为了协调性公理，定义如下：

定义2：假如风险X二级随机占优于Y，即X≻SSDY，则有ρ(X)≤ρ(Y)，则称风险度量ρ(X)是协调的。

Giorgi[14]在对风险度量公理进行研究后，给出了凸风险度量的概念。

定义3：如果风险度量ρ(X)满足：对于任意实数λ∈[0，1]，有ρ(λX+(1-λ)Y)≤λρ(X)+(1-λ)ρ(Y)，称风险度量ρ(X)为凸风险度量。

那么，所构造的风险度量ρ(X)=E(H(X-Y)+)具有哪些性质呢？在讨论之前，先介绍值函数的概念，将值函数定义为它的数学期望减去它的风险，即：

设F(x)为随机变量X的分布函数，X的值函数可以表示为如下积分：

性质1：设H(x)可导且满足0≤H′(x)≤1，若X≻FSD Y，则V(X)≥V(Y)。

证明：设X与Y为两个随机变量，F(x)与G(x)分布为X与Y的分布函数。若X≻FSDY，为证明V(X)≥V(Y)，构造函数，则u(x)的导数为：

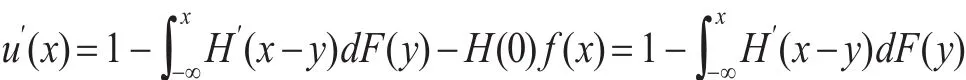
因 为H′(x)≤1,故 有dy≤1，所以u′(x)≥0 ，即u(x)是单调递增的。根据Ha⁃dar-russel定理，若X≻FSDY，则有Eu(X)≥Eu(Y)，即V(Y)。通过分部积分得到：

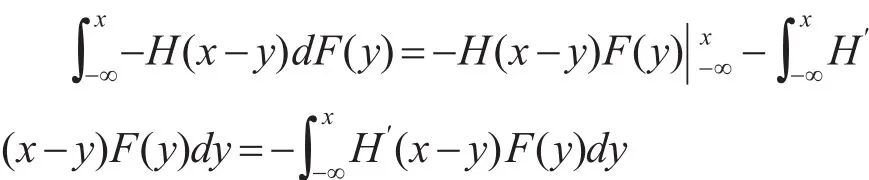
所以有：

因为X≻FSDY，所以F(x)-G(x)≤0 ，故有(x-y)(F(y)-G(y))dy≥0，假如存在x使得H′(x)＞0，则0 ，即：

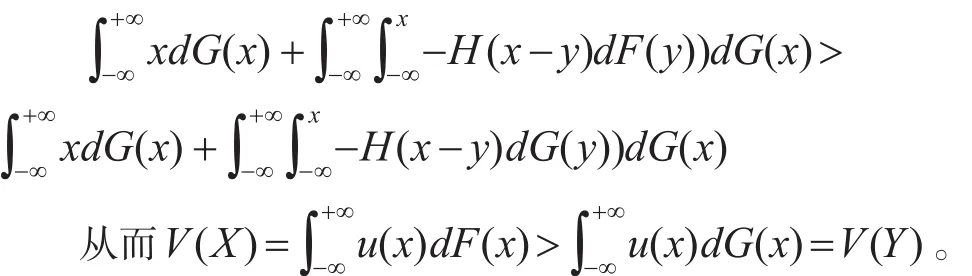
推论1：设H(x)可导且满足0≤H′(x)≤1，若X≻FSD Y，则对于任意实数λ(0≤λ≤1)，E(X)-λρ(X)≥E(Y)-λρ(Y)

证明：若X≻FSDY，E(X)≥E(Y)。由性质1，E(X)-ρ(X)≥E(Y)-ρ(Y)。从而有：(1-λ)E(X)≥(1-λ)E(Y)且λE(X)-λρ(X)≥λE(Y)-λρ(Y)，相加得到：E(X)-λρ(X)≥E(Y)-λρ(Y)

称λ为风险规避系数，称E(X)-λρ(X)为决策函数。说明只要风险规避系数在0到1之间，决策函数与一级随机占优是一致的。

性质2：设H(x)二阶可导且满足 0≤H″(x)≤1，若X≻SSDY，则V(X)≥V(Y)。

证明：设X与Y为两个随机变量，F(x)与G(x)分布为X与Y的分布函数。若X≻SSDY，为证明V(X)≥V(Y)，构造函数，则u(x)的二阶导数为：

因为H″(x)≥0,H′(0)≥0 ，所以u″(x)≤0 。说明u(x)是单调递增且凹的。若X≻SSDY，根据Hadar-russel定 理 有，下 面 证 明，由于：

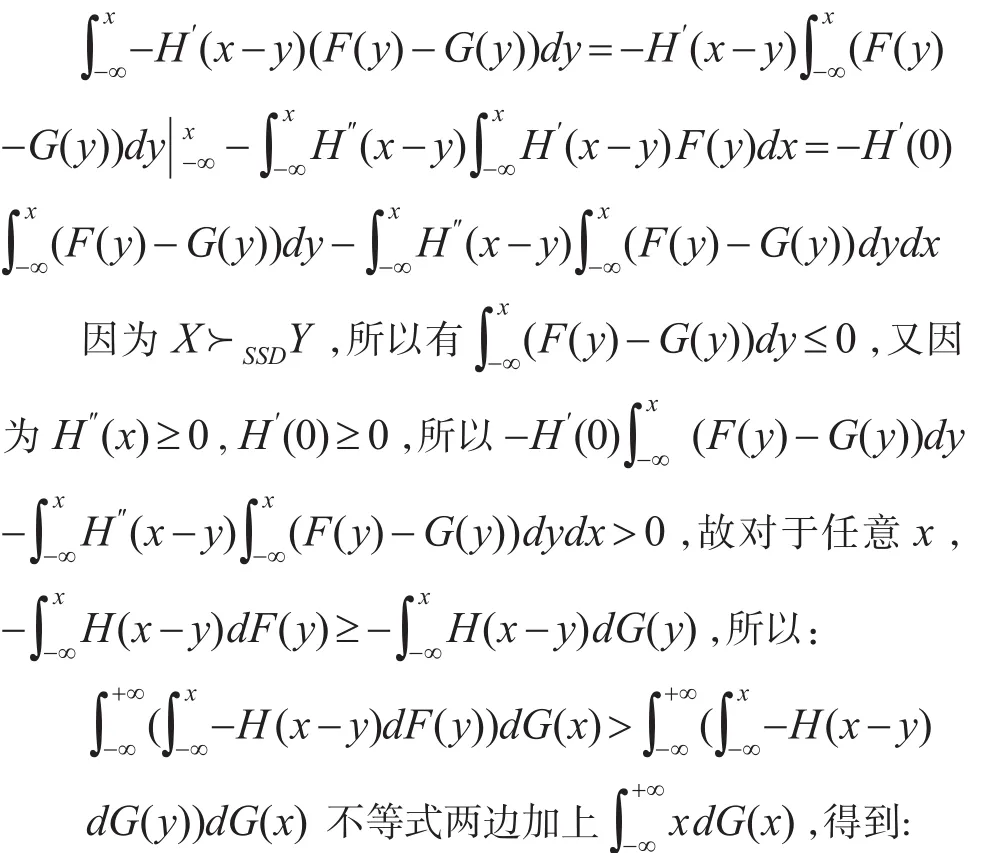
推论2：设H(x)二阶可导且满足 0≤H″(x)≤1，若X≻SSDY，则对于任意实数λ(0≤λ≤1)，E(X)-λρ(X)≥E(Y)-λρ(Y)

证明：若X≻SSDY，E(X)≥E(Y)。由性质2，E(X)-ρ(X)≥E(Y)-ρ(Y)。从而有：(1-λ)E(X)≥(1-λ)E(Y)且λE(X)-λρ(X)≥λE(Y)-λρ(Y)，相加得到：E(X)-λρ(X)≥E(Y)-λρ(Y)。

说明只要风险规避系数在0到1之间，根据决策函数所做的决策与二级随机占优也是一致的。

性质3：风险度量ρ(X)=E(H(X-Y)+)为凸风险度量。

证明：因为ρ(λX+(1-λ)Y)=E(H(λX+(1-λ)Y-λX′-(1-λ)Y′)+)，其中，X′是与X独立同分布的随机变量，Y′是与Y独立同分布的随机变量。由于(λX+(1-λ)Y-λ X′-(1-λ)Y′)+≤λ(X-X′)++(1-λ)(Y-Y′)+，而H(x)为一定义在R+上的单调递增的凸函数，故有：ρ(λX+(1-λ)Y)=E(H(λX+(1-λ)Y-λX′+(1-λ)Y′)+) ≤E[H(λ(X-X′)++(1-λ)(Y-Y′)+)]≤E[(λH(XX′)++(1-λ)H(Y-Y′)+]=λEH(X-X′)++(1-λ)EH(Y-Y′)+=λρ(X)+(1-λ)ρ(Y)

所以，ρ(X)=E(H(R-X)+)为凸风险度量。

综上所述，建立在风险度量方法ρ(X)=E(H(X-Y)+)上的值函数V(X)，当凸函数满足一定条件时不仅与一级随机占优是一致的，还和二级随机占优是一致的，这样根据值函数V(X)所做的决策与期望效用理论也是一致的。

3 结论

本文通过对Markowitz提出的方差以及Yamazaki提出的Gini系数的研究发现，这两种风险度量方法从本质上其实是随机变量到自身的距离，只不过距离的定义有所不同罢了。既然随机变量到自身的距离可以作为投资的风险度量，具有广泛性的H-平均距离也可以作为投资的风险度量。所以本文首先定义随机变量的风险度量为H-平均距离，但这样给出的风险度量与随机占优之间一般来讲是不一致的，而且也不属于下侧风险范畴。基于上述两点原因，本文将风险度量定义为随机变量到自身的下侧H-平均距离。下侧H-平均距离作为风险度量较之H-平均距离作为风险度量有很多优良特性。首先，下侧H-平均距离作为风险度量是凸风险度量，但H-平均距离作为风险度量则不是，因为方差就不是凸风险度量。基于凸风险度量在组合投资中的重要意义，所以，将风险度量修正为随机变量到自身的下侧H-平均距离是必须的。其次，H-平均距离作为风险度量一般与随机占优是不一致的，这点从方差上就可以看出。而下侧H-平均距离作为风险度量就不同了，研究发现建立在该风险度量方法上的值函数当满足某些条件时，不仅与一级随机占优是一致的，还和二级随机占优是一致的，这样根据值函数所做的决策与根据期望效用理论所做的决策也是一致的。鉴于以上两点，基于下侧H-平均距离的风险度量具有一定的研究价值和实际意义。