GM(1,1)模型与DEA结合对数据滞后系统的效率评价
方 炜,杨 步
(西北工业大学 管理学院,西安 710072)
0 引言
自从A.Charnes、W.W.Cooper等学者在1978年提出DEA模型以来,该方法已运用到对很多系统进行效率评价[1-3],评价结果对于系统如何合理地分配和利用资源具有重要的指导意义。但是在对系统效率进行评价的时候,它们都是在已知投入、产出的情况下进行DEA分析,并未考虑由于数据滞后导致数据未知系统的效率如何评价。文献[4-6]考虑到了产出相对投入具有滞后性的问题,它们首先分别利用不同方法来确定滞后期,然后再建立滞后产出与投入的DEA评价模型,最后进行效率评价,但是它们的研究也是建立在已知投入、产出的情况下进行效率评价,只不过此时的产出与投入不在同一个时间点上。但是现实中有时需要对一些因数据滞后而导致数据未知的系统进行效率评价以期指导未来投入、产出活动,这种对象见于科研活动、营销活动等。此时经典的DEA已无法对此类对象进行效率评价。
基于此,本文首先阐述了GM(1,1)模型与DEA的基本原理,在此基础上建立了数据滞后系统的效率评价模型,最后利用该模型并选取江苏省高等院校科研活动作为研究对象进行实证分析,以验证方法的可行性与实用性。
1 基本原理
1.1 灰度预测过程
设X(0)为原始非负序列:
利用GM(1,1)模型进行预测前,首先需要对X(1)进行准指数检验[7]
其中若存在m,当k>m时,有σ(1)∈[1,1.5),则称X(1)从k>m以后满足准指数规律。若不满足则可通过提高原始序列光滑度的方法提高光滑度后再建模,具体可参考文献[8-10]。若满足准指数规律则可以利用如下过程建立GM(1,1)预测模型:
Z(1)为X(1)的紧邻均值生成序列:
其中:
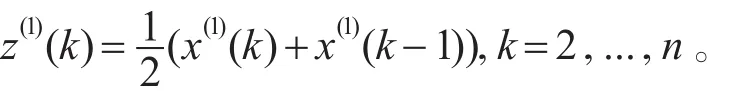
称x(0)(k)+az(1)(k)=b为GM(1,1)模型的基本形式。
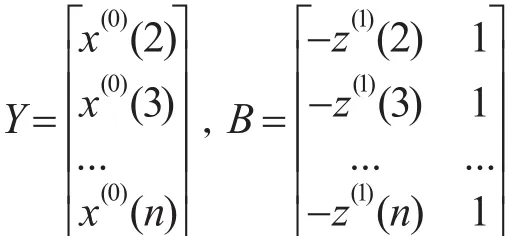
建立关于X(1)的一阶非齐线性微分方程,利用最小二乘法求得a,b。
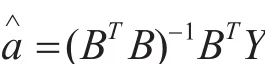
代入解得的一阶非齐线性微分方程得灰色预测模型为:
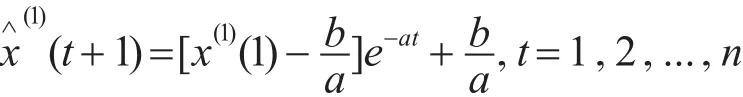
还原值可由下式得出:

得出预测值后还需对模型进行精度校验,以验证模型是否符合预测条件,计算过程如下:
(1)残差:
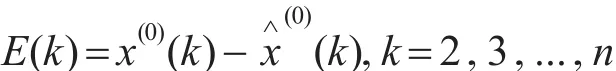
(2)残差均值:

(3)残差的方差:

(4)原数据方差:

(6)小概率误差预测精度检验等级参照表1。
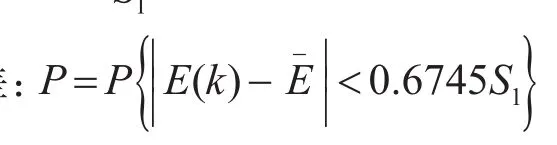
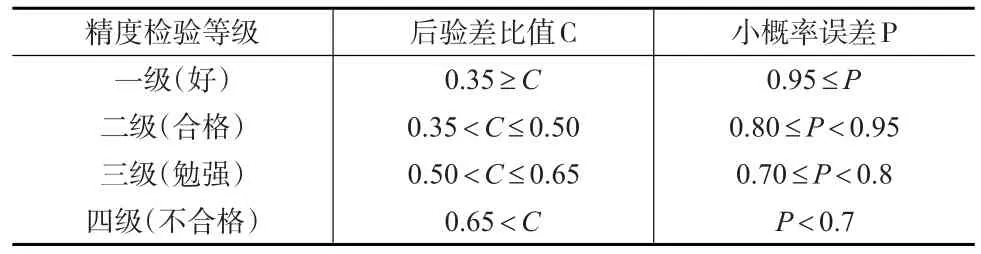
表1 精度检验等级
若模型不满足预测精度,则可通过残差修正、初始值修正及背景值修正等来提高预测精度,直至达到预期预测等级。
1.2 数据包络分析
Charnes等(1978)[11]应用数学规划模型将有效性度量方法推广到多投入多产出情形,提出C2R模型。
假设有n个决策单元,记为DMU1,DMU2,…,DMUn,每个决策单元有m种投入和s种产出,第j个决策单元DMUj的投入和产出向量分别为xj=(x1j,x2j,...,xmj)T,yj=(y1j,y2j,...,ysj)T,j=1,2,...,n。
设有待评价的决策单元DMUj0的投入产出为(xj0,yj0)T,简记为 (x0,y0)T,评价DMUj0有效性的C2R模型的对偶模型为:
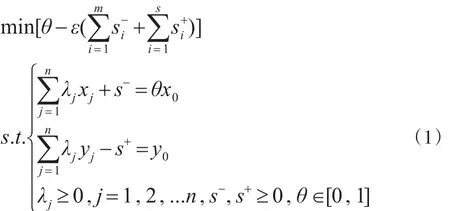
可由模型的最优解计算出θ,λ,s-,s+,由于C2R模型是在假设规模收益不变的情况下建立的,所以此时的效率值θ应为综合技术效率(TE),若θ=1,s-,s+=0,则决策单元是DEA有效的,同时为技术有效和规模有效;若θ=1,存在或,则决策单元是弱有效的,即该决策单元若将第i项投入减少或将第p项产出增加,该决策单元就可变为有效决策单元;若θ<1,则决策单元无效,可通过投影分析构造一个新的决策单元),使之成为有效决策单元,其中,同时可计算出,则决策单元规模收益不变,则决策单元规模收益递增,,则决策单元规模收益递减。
1.3 数据滞后系统的效率评价模型
假设要对一个具有n个决策单元(决策单元是基于时间序列的单元)的系统进行效率评价,若存在第1至p(p<n)个决策单元的m种投入与s种产出已知,而由于数据滞后因素导致第p+1至n个决策单元的i(1≤i≤m)种投入或j(1≤j≤s)种产出未知,现在要对整个n个决策单元进行DEA评价。
根据上文所述理论,首先根据已知的第1至p(p<n)个决策单元的m种投入与s种产出预测出第p+1至n个决策单元的i种投入或j种产出,得到第1至n个决策单元的m种投入与s种产出值,记为,其中,j=1,2,...,n,然后建立数据滞后系统的效率评价模型如下所示,并计算出相关指标进行效率评价。

其中各变量含义与式(1)相同。
2 实证
高校的科研活动是一个具有多投入与多产出且产出相对投入滞后的一个系统,本文数据来源于教育部科学技术司编制的2008—2015年《高等学校科技统计资料汇编》,选取江苏省高等学校科研活动作为本文研究对象。同时参考相关文献选取科技人员、科研经费数作为投入指标;申请专利以及发表论文数作为产出指标[12]。其中科技人员包括:教学与科研人员、研究与发展人员。科技经费包括:政府资金、企事业单位委托资金和其他。首先利用2010—2014年投入、产出数据预测出2015—2016年相关数据,然后再进行DEA分析,最后得出结论。
根据数据收集及整理得出2010—2014年江苏省高等学校科研投入、产出相关数据,如表2所示。
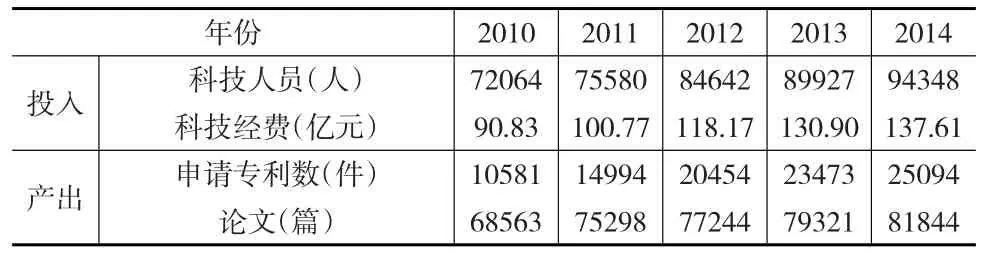
表2 江苏省2010—2014年高等学校投入产出数据
首先利用GM(1,1)对科技人员数进行预测,在预测前先做准指数检验,经计算得出σ(1)={2.0488 1.5733 1.3871 1.2928},当k>3时满足准指数条件,因此可以对X(1)建立GM(1,1)模型。经预测得2010—2014年的模拟值与2015—2016年的预测值={72064 77190 82843 88910 95421 102410 109910},平均相对误差为1.3%。光滑度,取a=0.01,得到变换后的数据为{0.9115 0.9083 0.9055 0.9043 0.9037},再进行光滑度检验得σ(1)={1.9965 1.4976 1.3318 1.2490},当k>2时满足准指数条件,因此可以将变换后数据进行灰度预测。经预测并还原得2010—2014年的模拟值与2015—2016年的预测值平均相对误差为4.88%。
最后对发表论文数进行预测,进行准光滑度检验得σ(1)={2.098 1.537 1.359 1.272},当k>3时满足准指数条件,因此可以对X(1)建立GM(1,1)模型。经预测得2010—2014年的模拟值与2015—2016年的预测值X^(0)={68563 75191 77305 79478 81712 84009 86371},平均相对误差为0.12%。
由于所有预测数据均可靠,所以接下来可利用以上预测数据与已知数据进行DEA分析。
根据DEA进行分析时要求决策单元个数要大于投入产出指标和两倍,本文选取江苏省已有高等院校科研数据和预测数据,即2007—2016年高校科研投入、产出数据进行DEA分析,使用相关软件计算得到结果如表3和表4所示。

表3 江苏省2007—2016年高等学校科研效率
对科技经费进行预测,先做准指数检验得σ(1)={2.1094 1.6168 1.4226 1.3123},当k>3时满足准指数条件,因此可以对X(1)建立GM(1,1)模型。经预测得2010—2014年的模拟值与2015—2016年的预测值X^(0)={90.83 104.30 115.18 127.19 140.45 155.10 171.27},平均相对误差为2.19%。
对申请专利数预测,做准指数检验得σ(1)={2.42 1.80 1.51 1.36},由于当k>4时才满足条件,为使得预测结果更加精确,需要改进原始序列光滑度以使其更好地满足准指数检验。本文参考文献[10]提出的方法来改进原始序列

表4 各决策单元投入产出指标的松弛变量取值
通过利用2010—2014年投入、产出数据对2015—2016年投入、产出数据进行预测并利用DEA评价后发现,2015年江苏省高等学校科研活动相对无效而2016年相对有效,由于2015年的科研活动已结束,所以对于该年的投入与产出已不能做出调整,而2016年的科研活动正在进行,所以上述结论对于指导江苏省2016年及以后高校科研活动具有重要意义,具体意义如下:
(1)指导未来活动
按照GM(1,1)模型预测得出的2016年的投入产出数据进行评价后发现DEA有效,所以如果江苏省2016年高校科研活动按照预测得出的数值进行投入、产出规划,那么势必最终会达到一个好的效果,这为江苏省政府确定2016年高校科研经费、科技人员投入量以及申请专利、发表论文产出量提供了清晰的目标,避免凭经验式的主观决策。同时若预测得出的数据进行评价时出现2016年相对无效,那么利用投影分析可将无效决策单元转变为有效单元,这样可及时调整投入、产出数,使得江苏省高校科研活动朝着相对有效的方向发展。
(2)明确无效原因
从评价结果来看,江苏省高校的平均综合效率为0.98652,平均纯技术效率为0.9983,平均规模效率为0.98822,三者值都比较高,这说明江苏省高校的科研活动比较有效,但仔细分析可以发现,在DEA无效年份中有3年无效是因为规模无效导致的,有1年无效主要是因为规模无效导致的,而只有2年无效是因为技术无效导致的,这说明江苏省高校科研活动的技术效率已达到相对较好状态,即科技产出相对科技投入已达到最大化但同时也需更好地加强管理使资源利用率更高。规模效率相对偏低且在规模报酬递增、不变、递减之间波动,这要求政府在确定高校科技投入时要确定好由递增到递减的零界点,可通过调整科技经费与科研人员数量来使科技活动处于规模报酬不变状态。
(3)摸清管理重点
在效率相对无效的年份中,其中产出不足都集中在申请专利数,而投入冗余都集中在科技经费上,这说明江苏省在申请专利数以及科技经费分配方面需要加强重视,这是导致高校科研效率相对无效的关键因素,要提高科研效率首先要加强对这两方面的管理,因此在“大众创业,万众创新”的环境下需多出台一些相关政策鼓励高校科技创新及申请专利,以便提高全省科技创新能力,另外在科技经费方面也要做好合理分配,避免出现科技经费拨款数过多导致科研效率低下的现象,另外各高校也需合理利用科技经费,尽可能将有限的经费创造出更大的价值。
3 总结
本文将GM(1,1)模型与DEA相结合提出了数据滞后系统效率的评价方法,然后选取江苏省高等学校科研活动进行实证分析,分析发现2015年江苏省高校科研活动无效而2016年科研活动有效,这为江苏省2016年高校科研活动更好地开展提供了指导思想,同时也验证了本评价方法的可行性与实用性。另外,若想对2016年以后年份进行投入产出规划,则只需先利用以往数据预测该年投入、产出数据,然后再利用DEA进行分析,最后可得出该年有效的投入、产出规划值。除此之外,该方法对于评价其他数据滞后系统的效率也同样适用。

