参数模型的预检验几乎无偏两参数估计

常新锋，王和祥，左秀霞

（江苏大学 财经学院，江苏 镇江 212013）

0 引言

考虑参数模型：

其中，y是n×1的观测向量，X是n×p的观测矩阵，β是p×1的未知参数向量，ε是n×1的随机误差向量，ε～N(0，σ2I)，σ2＞0。

模型(1)中β的附加信息为以下等式约束：

其中r为q×1的已知向量，R为q×p的矩阵，且q＜p。

对于模型（1），当不能确定等式约束条件式（2）是否成立时，考虑假设检验：H0:r=Rβ，H1:r≠Rβ。关于以上问题，其对应的似然比检验统计量为C=X′X，δ=Rβ-r。当H1成立时，统计量F为自由度为(q，n-p)的非中心F分布，非中心参数为(1 2)Δ，其中

对带等式约束条件的参数模型（1），Judge和Bock[1]提出了基于F检验的预检验估计。考虑模型存在复共线性的情况，Saleh和Kibria[2]提出了基于F检验的预检验岭估计。Yuksel和Akdeniz[3]得到了基于F检验的预检验Liu估计。Kibria和 Saleh[4]，Saleh[5]，Yang 和 Xu[6]等对各类预检验估计的统计性质进行了分析。Chang和Yang[7]提出了在t分布下基于W、LR和LM检验的预检验两参数估计。本文在Wu和Yang[8]提出的几乎无偏两参数估计的基础上，结合预检验估计的思想，提出了预检验几乎无偏两参数估计，并在均方误差准则下对估计的统计性质做了研究。

1 估计的提出

为了解决参数模型（1）中的复共线性问题，Wu和Yang[8]提出了几乎无偏两参数估计，其表达式为：

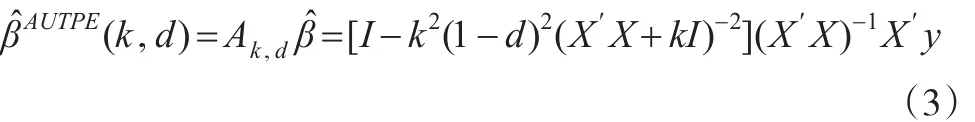
结合Kaciranlar等[9]得到约束最小二乘估计的方法，本文提出如下的约束几乎无偏两参数估计：

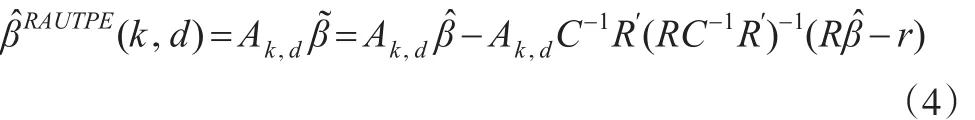
当不能确定等式约束条件式（2）是否成立时，本文得到基于F检验的预检验几乎无偏两参数估计

其中I(A)为事件A的示性函数，Fα表示自由度为(q，n-p)的中心F分布的上α分位数。

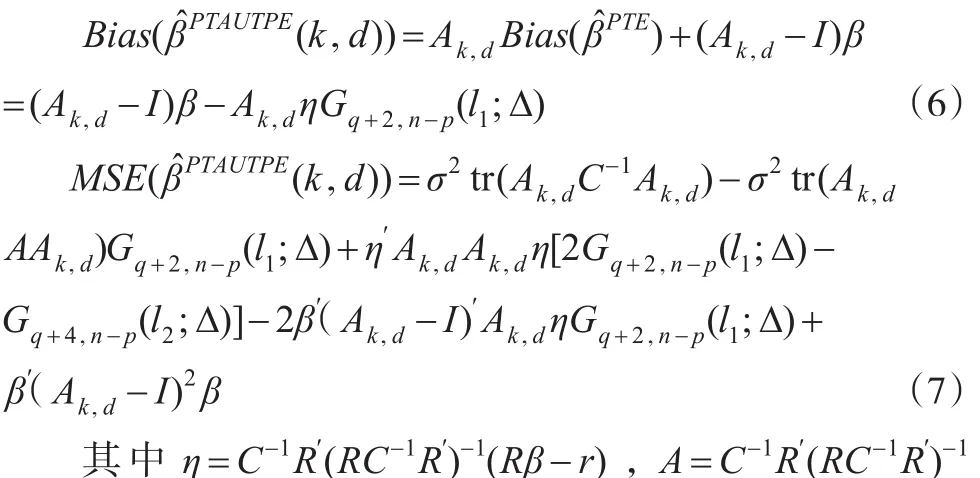
2 估计的性质

2.1 估计的均方误差值为Δ的函数

引理1[10]：设矩阵A，B均为n×n的实对称阵，且B为正定矩阵，对任意n×1的非零向量x，有≤λ1(AB-1)成立，其中λ1(AB-1)和λn(AB-1)分别表示矩阵AB-1的最大特征值和最小特征值。

定理1：在均方误差准则下，令k＞0和0＜d＜1不变，

证明：β̂AUTPE(k，d)的均方误差为：

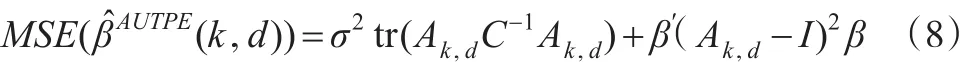
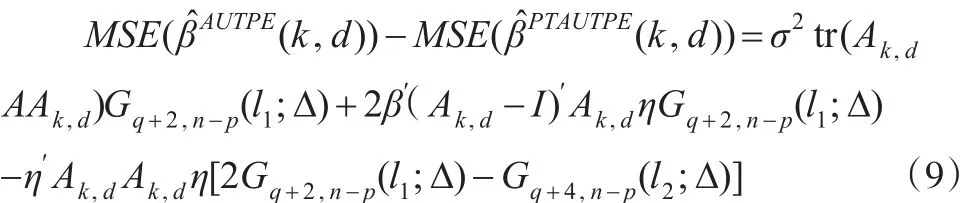
故MSE(β̂AUTPE(k，d))-MSE(β̂PTAUTPE(k，d))≥ 0 当且仅当：

根据引理 1，得σ2Δλp(Ak，dAk，dC-1)≤η′Ak，dAk，dη≤σ2Δλ1(Ak，dAk，dC-1) 。 其 中 Δ=σ-2η′Cη，λ1(Ak，dAk，dC-1) ，λp(Ak，dAk，dC-1)分别表示矩阵Ak，dAk，dC-1的最大特征值和最小特征值。因此MSE(β̂PTAUTPE(k，d))≤MSE(β̂AUTPE(k，d))成立的一个充分条件为Δ≤Δ1，其中：

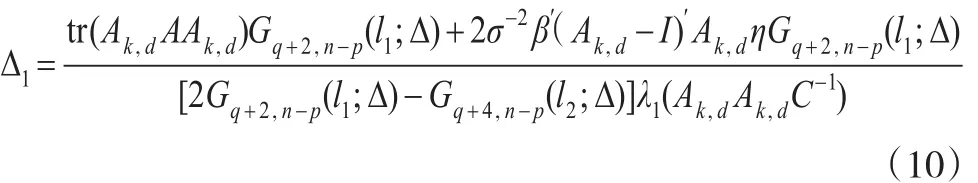
MS成立的一个充分条件为Δ≥Δ2，其中：

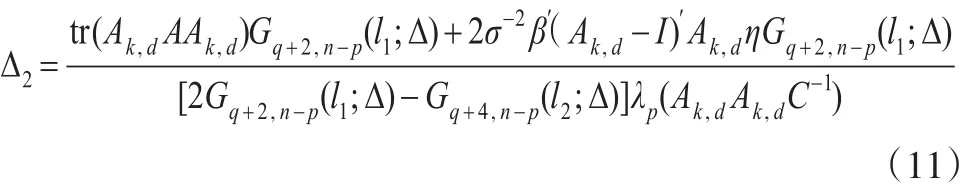
定理2：在均方误差准则下，令k＞0和0＜d＜1不变，当当

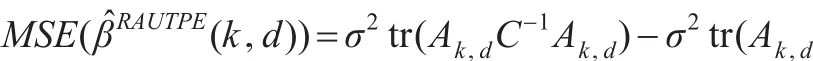
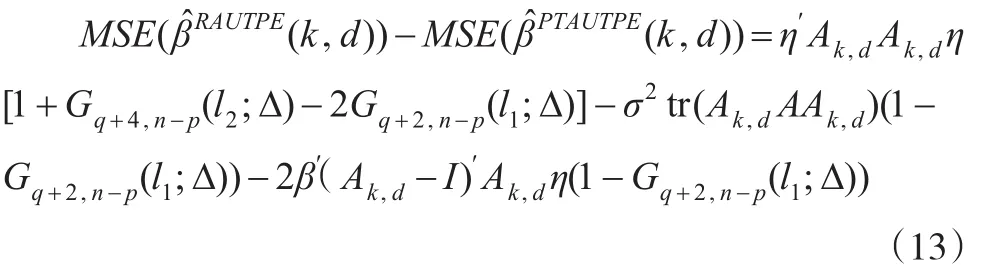
故MSE(β̂RAUTPE(k，d))-MSE(β̂PTAUTPE(k，d))≥ 0 当 且仅当：

M成立的一个充分条件为Δ≤Δ4，其中：

2.2 估计的均方误差值为参数k和d的函数

另矩阵P为正交矩阵，且满足其中λ1≥…≥λp＞0为矩阵C的顺序特征根。则式（9）和式（12）分别记为：

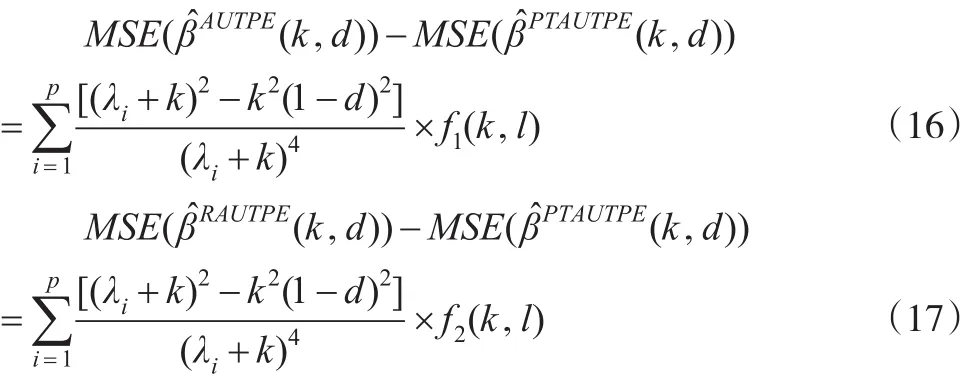
定理3：

（1）在均方误差准则下，令 Δ＞0和 0＜d＜1固定，h1i＞0 ，当 0＜k＜k1时，MSE(k，d))≤(k，d)) ；当k＞k2时 ，(k，d))。

（2）在均方误差准则下，对Δ＞0和k＞0固定，h2i＞0 ，当d1＜d＜1 时，d))；当 0＜d＜d2时，d))。

（1）令 0＜d＜1固定，f1(k，l)为参数k的函数，则若h1i＞0，此时关于参数k的一元二次函数f1(k，l)开口向下，其一正根为：

由于k=0 时，f1(0，l)=λi＞0 ，对任意的 0＜k＜k1，k1=min{k1i} ，有f1(k，l)≥0 ，故MSE(β̂PTAUTPE(k，d))≤MSE对任意的≤0 ，故

（2）令k＞0固定，f1(k，l)为参数l的函数，则当h2i＞0时，关于参数l的一元二次函数f1(k，l)开口向下，其一正根为，对 任 意 的 0＜l＜l1i，有f1(k，l)＞0 。 而l=1-d，对任意的，有对 任 意 的有f1(k，d)≤ 0 ，故

定理4：

（1）在均方误差准则下，令 Δ＞0和 0＜d＜1固定，h3i＞ 0 ，当k＞k3时，d))；当 0＜k＜k4时，d))。

（2）在均方误差准则下，令 Δ＞0和k＞0固定，h4i＞0 ，当 0＜d＜d3时，(k，d))；当d4＜d＜1时，(k，d))。

（1）令0＜d＜1固定，f2(k，l)作为k的函数，则：

f2(k，l)=h3ik2+f͂3i(2k+λi)

若h3i＞0，此时关于k的一元二次函数f2(k，l)开口向上，其一正根为：

其中

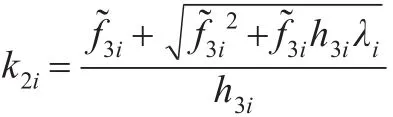
由于k=0 时，对任意的k＞k3，k3=max{k2i}，有f2(k，l)≥0 ，故对 任 意 的 0＜k＜k4，k4=min{k2i} ，有f2(k，l)≤ 0 ，故

（2）令k＞0固定，f2(k，l)为l的函数，则：

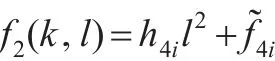
当h4i＞0时，关于l的一元二次函数f2(k，l)开口向上 ，其 一 正 根 为对 任 意 的l＞l2i，有f2(k，l)＞0。而l=1-d，对任意的对任意的0 ，故MSE

3 模拟分析

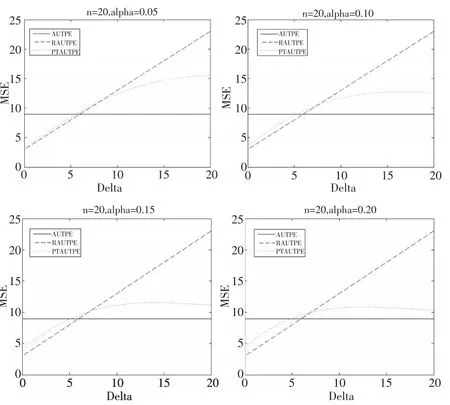
图1 k=0.2和d=0.8时各估计在不同显著水平下的均方误差

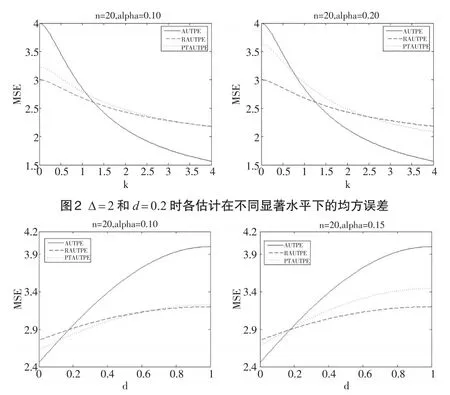
图3 Δ=2和k=0.9时各估计在不同显著水平下的均方误差

从图1发现，对于不同的α，β̂PTAUTPE(k，d)，β̂RAUTPE(k，d)和β̂AUTPE(k，d)的均方误差都随着参数 Δ 的变大而增大。当Δ取值接近于0时，估计β̂RAUTPE(k，d)的均方误差值小于估计β̂PTAUTPE(k，d)的值，同时估计β̂PTAUTPE(k，d)均方误差值小于估计β̂AUTPE(k，d)。随Δ值变大，估计β̂PTAUTPE(k，d)，β̂RAUTPE(k，d)和β̂AUTPE(k，d)的均方误差值的大小关系与上述情况相反。图1中的均方误差值变化情况验证了定理1和定理2。

从图2看出，对于不同的α，β̂PTAUTPE(k，d)，β̂RAUTPE(k，d)和β̂AUTPE(k，d)的均方误差都随着参数k的变大而减小。当k取较小值时，β̂RAUTPE(k，d)的均方误差值小于β̂PTAUTPE(k，d)的值，同时β̂PTAUTPE(k，d)均方误差值小于β̂AUTPE(k，d)。 随着参数k值变大，估计β̂PTAUTPE(k，d)，β̂RAUTPE(k，d)和β̂AUTPE(k，d)的均方误差值与上述情况相反。从图3看出，对于不同的α，β̂PTAUTPE(k，d)，β̂RAUTPE(k，d)和β̂AUTPE(k，d)的均方误差都随着参数d的变大而变大。当d取值较小时，β̂AUTPE(k，d)的均方误差值小于β̂PTAUTPE(k，d)的值，同时β̂PTAUTPE(k，d)均方误差值小于β̂RAUTPE(k，d)。随着参数d值变大，估计β̂PTAUTPE(k，d)，β̂RAUTPE(k，d)和β̂AUTPE(k，d)的均方误差值与上述情况相反。图2和图3中的均方误差值变化情况验证了定理3和定理4。

4 总结

本文结合几乎无偏两参数估计和预检验估计，提出了参数模型的预检验几乎无偏两参数估计。在均方误差准则下，分别给出了预检验几乎无偏两参数估计优于几乎无偏两参数估计、约束几乎无偏两参数估计的充分条件。通过数据模拟分析，验证了上述理论结果。