方差分析与回归分析的整合：虚拟变量与设计矩阵

郭少阳,郑蝉金,陈彦垒

（1.江西师范大学 心理学院，南昌 330022；2.聊城大学 教育科学学院，山东 聊城 252059）

0 引言

方差分析与回归分析同质么？面对这一理论问题，不少初学者甚至教学者都难以给出准确的答案。近年来，随着各类统计方法愈加多样复杂，如何掌握这些新兴方法成为了统计学习的一大难题，这既不符合统计学起源的初衷，也不利于实证科学的发展进步。为了加深对统计方法本身的理解，提高统计学习的效率，方法统一与模型整合日益成为当前统计学研究的一大热点[1-3]。

在社会科学的实证研究中，方差分析与回归分析作为最实用的统计方法，已被广泛应用于各个领域的数据分析当中。一般来讲，方差分析主要用于检验多个样本均值之间是否存在显著性差异，进而以样本推断总体；而回归分析的目的则是建立自变量与因变量间的作用模型，以便对未来做出理论预测[4]。表面上来看，这两种方法之间似乎并无关联，大多数统计教材也倾向于将这两种方法按照相互独立的章节分别论述，并未探讨二者的本质关系；但实质上，二者都在利用方差的可分解性，从总变异中分解出所需的目标变异及误差变异，其解决问题的方法及思路是一致的，这种内在联系天然蕴含在两种方法当中。正如t检验可以看作是F检验的一个特例，本文认为，方差分析也可以看作是回归分析的一个特例，通过虚拟变量及设计矩阵，可令方差分析与回归分析实现统一。

1 方差分析与回归分析的统计模型

首先，以单因素方差分析为例，其统计模型与虚无假设为:

其中Yij表示第j个处理水平上第i个被试的得分，μ表示总体均值，μ1至μj表示各组均值，αj表示第j个水平的处理效应，eij是一个服从正态分布的随机误差。方差分析假定任意被试只受其所在处理水平的影响，那么，便可将模型改写为另一种等价形式：

即：

其中U=，E为随机误差。

同时，多元回归分析的基础统计模型为：

显然，改写后的方差分析模型（3）与多元回归模型（4）非常相似，这就意味着，可以尝试对回归分析的自变量矩阵X进行改造，来使两种方法得以整合，也就是所谓的“以回归的方式做方差分析”。

2 虚拟变量与设计矩阵

虚拟变量，又称哑变量，是对客观事物进行量化处理的一种人工编码形式，虚拟变量的引入虽然会令回归模型更加复杂，但却极大地简化了模型解释的问题[5]。要整合方差分析与回归分析，首要问题便是如何使用虚拟变量令回归截距等于总体均值（即处理效应之和，回归系数代表组与总体均值之差（即αj=μj-μ）。举例来说，通常使用二分法（1,0）对自变量性别进行虚拟编码，以0表示参照组（如女性），1表示观察组（如男性），假设以月收入作为因变量进行一元回归分析，得到回归方程:月收入=3000-500×性别。此时，截距3000即为女性月收入，-500则是男女月收入之差。显然，这种编码方式着重考察组间差异，其截距等于参照组的组均值，回归系数代表组间收入差值，适用于进行事后检验或简单效应检验，但却不符合方差分析整体检验的基本要求。要解决这一问题，最简单的方式便是将参照组的0转码为-1，使虚拟变量的均值为0，重新进行回归，便可使截距及回归系数的含义与方差分析一致：截距等于总体均值，斜率等于处理效应。若将这种二分法的编码思路扩展到多组比较之中，便可得到回归分析的设计矩阵。

所谓设计矩阵，是一种由观测结果中的所有解释变量的值构成的矩阵，能够形象简练地表示理论假设或实验处理中的设计构想，在回归分析中，可用于处理自变量为分类变量时的建模问题。为了方便论述设计矩阵的构造方法及实例分析，本文援引舒华[6]在论述两因素完全随机设计时使用的实验数据，如表1所示，该数据包含24名被试在A（a1,a2）×B（b1,b2,b3）6种处理水平上的实验结果。

表1 实验数据

3 单因素方差分析及其设计矩阵

将虚拟变量扩展为适用于多组比较的设计矩阵较为复杂，本文将以单因素三水平方差分析为例（仅考虑表1中的B因素）进行论述。首先，若某个因素有三个水平（b1,b2,b3），使用二分法判断任意单个被试是否接受任意处理的水平时，其判断结果将以列向量的形式保留。例如，(1,0,0)T，(0,1,0)T，(0,0,1)T分别表示某被试仅接受了 b1，b2或b3水平的处理，观察三个向量可以发现，末尾列向量(0,0,1)T的判断结果完全受制于其他向量，它所包含的信息是重复且多余的，故而可将其直接舍弃，换言之，判断结果的自由度为处理水平数减1，本例中即为2个自由度。其次，在多组比较时，二分法以在所有水平编码均为0的组作为参照组，并以参照组均值作为多组比较的基线，正如前文所述，要以总体均值作为基线，需要将参照组进行转码，即(1,0,-1)T，(0,1,-1)T。最后，将被试按照处理水平进行排序，扩展包含虚拟编码的列向量，便可得到一个包含全部被试及其处理情况的设计矩阵：

其中，角标为该处理水平拥有的被试数量，本例中代表包含8个相同主元素的列向量。若使用该设计矩阵对因变量Y进行回归，得到回归方程：

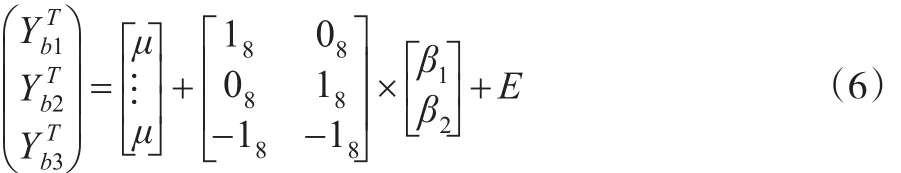
其中β1表示b1水平的处理效应，也就是b1水平组均值与总体均值之差；β2表示b2水平的处理效应，b3水平的处理效应β3可由回归方程推导得出，即：β3=-β1-β2；与此同时，回归系数的有效性检验也等价于检验处理效应是否显著。为了验证推导结果是否正确，本文使用SPSS 20.0分别对表1中的数据进行方差分析及回归分析（自变量为设计矩阵），对比两种分析的处理结果。

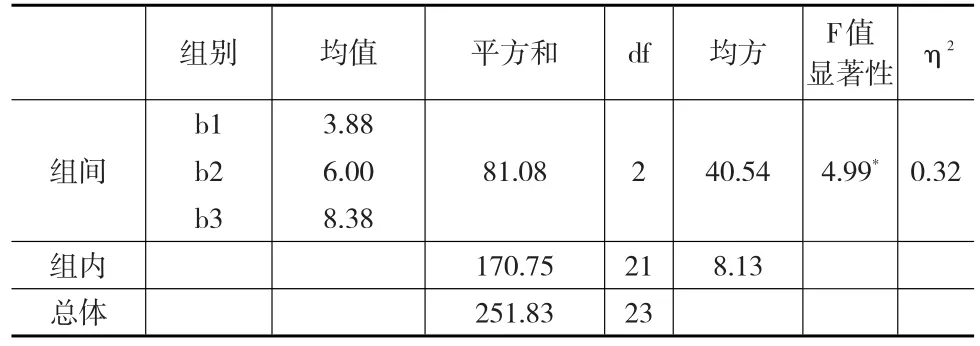
表2 单因素方差分析表(＊p＜0.05)

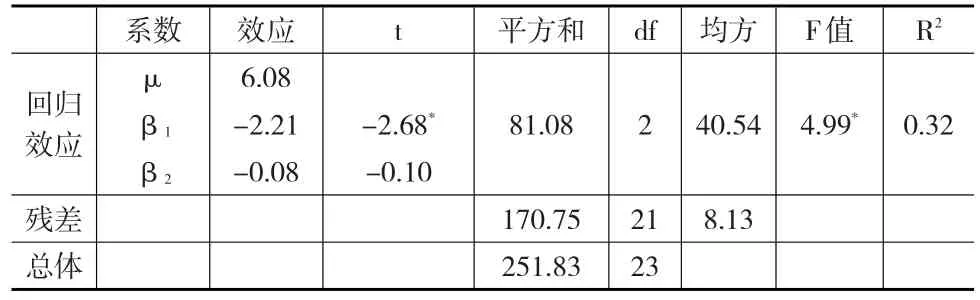
表3 单因素设计矩阵回归分析表(＊p＜0.05)

如表2和表3所示，两种方法所得到的处理效应、F值，以及效果量(η2与R2)完全一致，至此，本文便以设计矩阵为中介，实现了回归分析与单因素方差分析的统一。

4 两因素方差分析及其简单效应检验

4.1 综合的F检验

相较于其他统计方法，方差分析的最大优势便是可以用于处理多变量间复杂的交互作用，那么，能否利用设计矩阵在回归方程中实现交互作用分析呢？本文首先借鉴一下回归分析中调节效应检验的基本方法[7]。所谓调节效应，就是考察自变量何时影响因变量或自变量何时对因变量的影响最大，其基本的统计模型为[8]：Y=U+γ1X+γ2M+其中X，M均为中心化连续变量，MX的乘积表示调节效应，回归系数γ3表示调节效应大小。温忠麟等[8]认为，调节效应可以看做是交互作用的一个特例，故而可以尝试将这种乘积法的思路推广到设计矩阵的构造中。

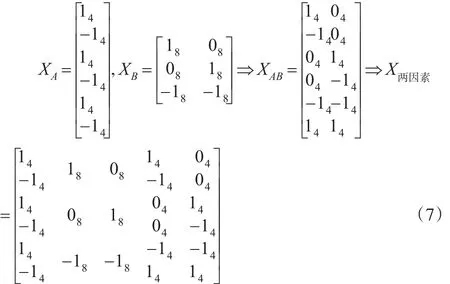
如公式（7）所示，首先，依据表1中A，B两个因素各自的处理水平，分别构造两个独立的单因素设计矩阵（使用相同的数据排序方式）；之后，将XA中各列向量所属元素依次与XB中各列向量对应元素两两相乘，由此可得到乘积矩阵；最后，将三个矩阵依次合并，便得到了完整的设计矩阵，其对应的回归方程为：

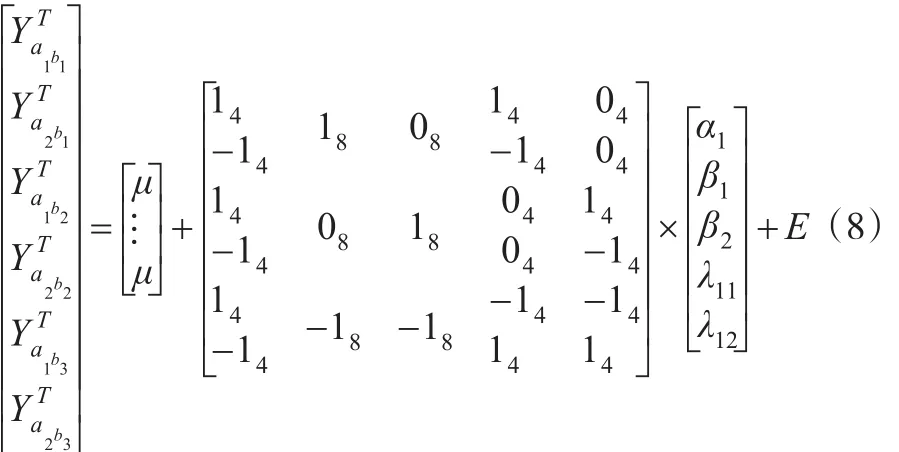
其中α1表示a1水平的处理效应，也就是a1水平组均值与总体均值之差；β1，β2分别表示b1和b2水平的处理效应；λ11和λ12表示a1b1，a1b2与总体均值之差。同理，可由方程α2，β3，以及相应的交互作用λ13，λ21，λ22和λ23。为验证推导结果，本文同样使用SPSS对表1中的数据进行二因素方差分析及相应回归分析。

如表4和表5所示，如使用完整的设计矩阵进行回归，则仅能得到一个整体的回归及残差平方和，也就是相当于方差分析中的组间及组内效应，要得到每个因素单独的平方和，需要将各因素的设计矩阵分别独立的进行回归，并使用统一的整体残差平方和计算F值。当然，这仅仅是理论上二者相互转化的一种关系，在实际应用中，研究者无需额外关注回归分析中各因素的回归平方和，仅需要通过回归系数的有效性检验，便可以直接判断主效应及交互作用是否显著。

表 4 两因素方差分析表 (＊＊＊p＜0.001)

4.2 简单效应检验

至于简单效应检验，由于其虚无假设发生改变，故而设计矩阵也要加以变化。事实上，简单效应检验是一种边际化的交互作用分析，以B因素在a1的简单效应检验为例，统计分析的核心由两因素的整体关系变为了某一水平与另一因素的关系。因此，需要边际化交互作用矩阵XAB，排除A因素中其他水平的作用，如a2。如公式（9）所示，要实现这一目的，仅需将A因素的设计矩阵复原为（1,0）编码，其中1表示待检验处理水平，0表示其他水平，然后与B因素设计矩阵对应相乘，就得到了简单效应检验的设计矩阵。从表4和表5中可知，两种方法产生的简单效应平方和完全一致，至此，多因素方差分析与回归分析的模型统一得以实现。

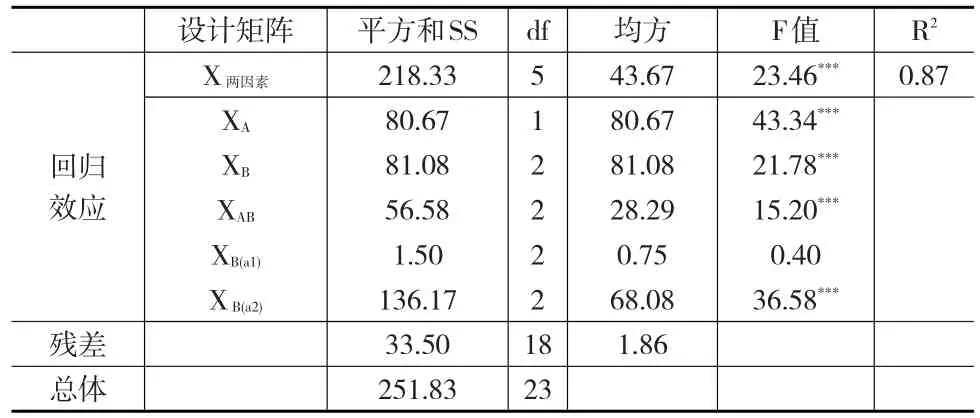
表5 两因素设计矩阵回归分析表 (＊＊＊p＜0.001)

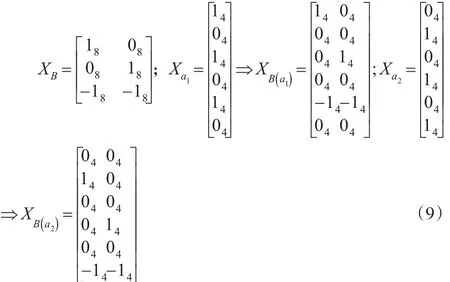
4.3 事后检验与多重比较

正如前文所述，方差分析是一种综合的整体检验，在研究者拒绝原假设之后，数据分析的关注点也从处理效应与均值之间的差异转变为各组之间是否存在显著差异，也就是方差分析体系下的事后检验及多重比较。严格来说，这些后续的步骤已经超出了方差分析的检验范畴，普遍使用诸如LSD，S-N-K等方法对各个水平进行两两比较。事实上，这些两两比较在回归分析的框架下，通过对回归系数的有效性检验，可以直接得到。

在综合的F检验中，本文将参照组的编码设置为-1以保障回归截距等于总体均值，使回归系数等于处理效应，其检验结果代表组均值与总体均值之间是否存在显著差异。在进行多重比较时，本文的关注点不再是组与总体，而是组与组之间的差异。因此，需要令回归截距等于参照组的组均值，即将-1转码为0，使回归系数代表观察组与参照组的离均差，于是，回归系数的检验结果便等价于事后检验的结果了。

5 讨论

5.1 方差分析与回归分析的本质关系

直观上来讲，回归分析的自变量通常为连续型数据，而方差分析的自变量则是分类数据，这种数据驱动所导致的刻板印象使统计学习者模糊了方差分析与回归分析的本质关系，将二者视为截然不同的两类统计方法。事实上，分类数据与连续数据之间存在一种递推的关系，研究者往往可以通过对详尽的连续数据进行人工划分来得到分类数据。反之，却无法由分类数据得到完整连续变量，也就是说，分类数据可以看作是连续数据的一个特例，本文使用虚拟变量及设计矩阵便是起到了数据转化的作用。正如皮尔逊积差相关与点二列相关在处理二分变量时结果一致，适用于处理连续变量的统计方法往往可以同时处理分类数据，这也是方差分析可由回归分析递推而来的底层因素。

就模型本身来看，方差分析与回归分析同属一般线性模型，其模型的基本形式都可表达为Y=XB+E，这就使得两种方法在本源上是相通的，使模型等价成为可能。在数据处理的层面，二者均采用平方和分解的形式进行分析，有所不同的是，方差分析致力于层层分解各个因素所导致的变异，而回归分析却通常仅考虑全部的预测源所带来的效应，即组间平方和等于回归平方和。因此，研究者需要使各因素分别独立地对因变量进行回归，得到各自的回归平方和，便可实现二者的统一了。综上所述，方差分析可以看作是回归分析的一个特例，其分析结果全部可由回归分析进行递推。

5.2 简练的计算过程

传统的方差分析具有一整套完备庞大的计算体系[6]，变量的增加和水平的变化都会影响到计算过程，使统计初学者备受困扰。虽然现阶段介绍方差分析的统计教材、专著非常丰富，但这并不能减少方差分析计算过程本身的复杂性。相比之下，回归分析几乎在任何情况下都可以使用统一的公式（最小二乘法，公式）得到计算结果，不受自变量或设计矩阵X变化的影响，计算过程简单明确，易于理解。因此，采用回归的方法做方差分析既有利于简化统计学习的难度，也有利于快速得到计算结果。

5.3 更具解释力的统计结果

方差分析所得到的统计结果通常是具有结论性质的，例如，组A与组B的均值存在显著差异；水平a1在B因素上不存在显著差异，这种单调乏味的统计结果往往很难给人以直观的感受，也不难从总整体的角度给出一个宏观的结果解释。相比之下，回归分析建立的统计模型更具解释效力，以前文中两因素实验设计为例（X两因素），其回归模型为：

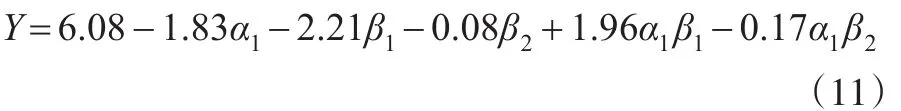
其中α1，β1，α1β1达到显著性水平。

通过这个回归模型，可以用简单代数的方式(1,0,-1)得到各组的处理均值，同时，由回归系数显著性检验的结果判断各处理效应是否有效。显然，回归分析在模型解释上比方差分析更为简练、直观，在复杂实验条件下更有利于研究者理解和把握统计结果。