贝叶斯网络及其在白酒安全预警中的应用
姜同强,莫名垚,任钊,王美洁
(1.北京工商大学计算机与信息工程学院,北京 100048)
(2.农产品质量安全追溯技术及应用国家工程实验室,北京 100048)
食品安全问题关系人们的生产生活和社会经济的发展,为了保证人们的饮食安全,提高政府监管效率,食品安全预警尤为重要。常用的食品安全预警研究方法有2种:定性分析和定量预测。定性分析即借助相关理论分析得出预警结论,如风险矩阵[1]、案例推理[2]等。定量预测即采用方法、模型分析食品的检测或监测数据,预测食品安全风险等级,如统计分析方法中的时间序列[3]、数据挖掘算法中的神经网络[4]等。本文用的数据和方法属定量预测法。
定量预测法存在以下问题:(1)统计分析方法需要已知系统结构或明确变量之间的关系[5]。(2)神经网络,作为食品安全预警研究的常用工具,存在网络训练效率不稳定的缺点[6]。(3)二者都是在风险达到临界点或即将到临界点时才进行警示,不能在已知数据看似正常的临界状态预测未来知识[7]。
贝叶斯网络(Bayesian Network,BN)既具有传统统计分析的功能,又能有效结合先验知识,在不完全信息下能稳定、准确地进行数据分析与预测。因此,可利用贝叶斯网络稳定、高效的统计分析与预测的能力进行食品安全预警,能有效解决现有研究中的问题。
同时,贝叶斯网络广泛应用于医学、制造业、城市交通和灾害监测等方面的预警研究,例如牟敬锋(2015)等运用贝叶斯网络构建了公共场所集中空调冷却塔水嗜肺军团菌污染预警模型[8];张翠侠(2015)等提出一种基于贝叶斯网络的机械加工车间碳足迹监测与预警方法,实现了机械加工车间碳足迹实时监测与动态预警[9];张铭(2016)等运用贝叶斯层次网络推断故障预警,对风险隐患快速定位[10]。金杉(2016)等利用贝叶斯网络算法设计了一种能实现全网信息融合的算法[11]。但贝叶斯网络在食品安全预警方面的研究还未引起广泛关注。
为避免统计分析方法研究背景要求高,神经网路训练不稳定的问题,弥补贝叶斯网络在食品安全领域的研究空白,本文以低度白酒作为研究对象,采用食药监局的监测数据,运用贝叶斯网络建立白酒安全预警模型,并与神经网络算法对比,验证模型的稳定性,辅助政府监管,丰富食品安全预警方法。
1 材料与方法
1.1 实验材料
本文使用的数据来源于食药监局 2016年低度白酒的监测数据。
白酒原始数据的预处理。简化数据属性,去除次要影响因索,如抽样人员、抽样单位等信息,如表 1所示。分析数据并选取14个检测项目(有:铬、铅、氨基甲酸乙酯、环已基氨基硫酸钠、纽甜、阿斯巴甜、糖精钠、乙酰磺胺酸钾、酒精度、氰化物、总酸、总酯、大肠菌群和甲醇)作为评价指标,该评价指标包含6类:金属污染物、农药残留、食品添加剂、品质指标、微生物污染、非食用物质。

表1 低度白酒安全检测原始数据Table 1 Raw data for safety detection of low-alcohol liquor
预处理数据的标准化。若结果判定为“合格项”,则将其标记为 1;若结果判定为“不合格项”,统计每种危害因子不合格记录的检测值超出可取最大上限值(或低于可取最小下限值)的百分比(以下简称超标百分比),再统计一定百分比范围内的频次,按频次划分不合格等级。统计数据表明:每种风险因子的可取值域不同,不合格记录的超标百分比也不同,但通常不会到200%。
评价指标中的危害因子的可取值域分为3类,即不得检出、一定数值范围内和需超过某个值。对不得检出项,如环已基氨基硫酸钠,设其超标百分比最大值为100%,不合格记录有46条,其中大于0 mg/kg且小于等于1 mg/kg的20条,轻度不合格项,标记为2,大于1 mg/kg且小于等于20 mg/kg的18条,中度不合格项,标记为3,大于20 mg/kg的8条,重度不合格项,标记为 4。对非不得检出项,如甲醇,超标百分比平均值为180%,不合格记录有9条,其中大于2 g/L小于等于4 g/L的7条,轻度不合格项,标记为2,大于4 g/L的2条,重度不合格项,标记为3。部分数据的离散标准值如表2所示。

表2 部分数据的离散标准值Table 2 Discrete standard values for partial data
白酒是非季节性食品,本文假定外界环境、政府政策、生产工艺对白酒影响保持稳定,选取2016年的6458组数据组数据作为实验数据,1~11个月的5922组数据作为训练集,12月的536组数据作为测试集。
1.2 实验方法
1.2.1 白酒食品安全状况等级与预警指标的建立
借鉴李克特量表[12]的思想,构建白酒食品安全风险等级与预警指标,如表3所示,贝叶斯网络中各关键危害因子的概率值已包含其对白酒食品安全状况问题发生的贡献大小,因此阈值指的是贝叶斯网络模型得到的白酒食品安全状况的概率值。

表3 白酒食品安全状况等级与预警指标Table 3 Food safety status and warning indicators of liquor
1.2.2 贝叶斯网络工作原理
贝叶斯网络是一种能将具体问题中的复杂变量关系在一个网络结构并反映变量的依赖关系的有向无环图模型,适用于表达和推理不确定性知识[13]。贝叶斯网络的组成有2部分:网络结构和条件概率表,因此贝叶斯网络模型的构建包含2个部分:结构学习和参数学习。
将白酒食品安全预警体系用贝叶斯网络表示为:B=(G,P),其中G=(V,E)表示有n个节点V={X1,X2,…,Xn}的有向无环图,根据评价指标体系可知,n为 21,V为评价指标中的危害因子集合,E为危害因子间的直接依赖关系。每个节点Xi∈V都附有一个条件概率分布P(Xi|pa(Xi)),pa(Xi)为Xi的父节点的集合。结合节点间的独立性和概率的链式规则得联合概率分布公式,如式(1)所示。

1.2.3 贝叶斯网络模型网络结构的建立

图1 白酒安全预警贝叶斯网络模型的网络结构Fig.1 Network structure of Bayesian Network model for liquor safety early warning
专家建模法是确定网络结构的方法中运用较多的方法,它根据先验知识,依据是否条件独立把危害因子绘制在一个图中而形成网络结构,且网络结构不存在环路。运用专家建模法,得到白酒安全预警贝叶斯网络模型的网络结构,如图1所示。
1.2.4 贝叶斯网络模型的参数学习
确定各节点概率的过程称为参数学习,适用的参数学习算法取决于网络结构是否已知和数据集合是否完整。极大似然估计算法是最常用的参数学习算法,适用于网络结构已知,数据集完整的情况。故本文采用最大似然算法对贝叶斯网络专家模型进行参数学习。贝叶斯网络由N个节点V={X1,X2,…,Xn}组成,不失一般性,设节点Xi共有ri个取值,其父节点π(Xi)共有qi个组合的取值。数据D是由样本{D1,D2,…,Dm}组成的完整数据集,即D={D1,D2,…,Dm},则网络的参数为:

其中i,k,j的取值范围分别为 1~n,1~ri,1~qi。
用θ记所有θijk组成的向量,则θ的对数似然函数为:
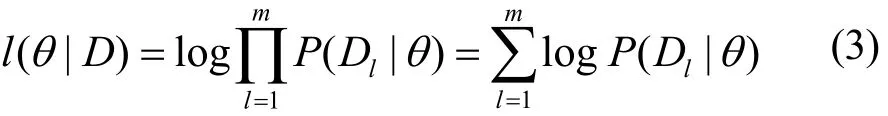
设样本Dl的特征函数χ(i,j,k:Dl)为:

设mijk是数据中满足Xi=k和π(Xi)=j的样本数量,则有:

则θijk的最大似然估计θ*ijk为:


表4 环已基氨基硫酸钠C1的概率分布Table 4 Probability distribution of cyclohexyl sodium sulfate C1

表5 甲醇F1的概率分布Table 5 Probability distribution of methanol F1

表6 非食用物质F的概率分布Table 6 Probability distribution of non-edible substance F
在白酒安全预警的贝叶斯网络模型中,共有 21个节点,即 N=21;根据预处理结果,最顶层(即无父节点)的节点有其对应的离散化取值,“白酒食品安全状况”节点共有4个取值。
为简化模型复杂度,其余节点均共有2个取值,即1为合格,2为不合格。数据D由5922组数据组成,即D={D1,D2,…,D5922}。结合食药监局的历史数据,统计分析,可得各个节点的先验概率,部分危害因子的先验概率如表4~表7所示。
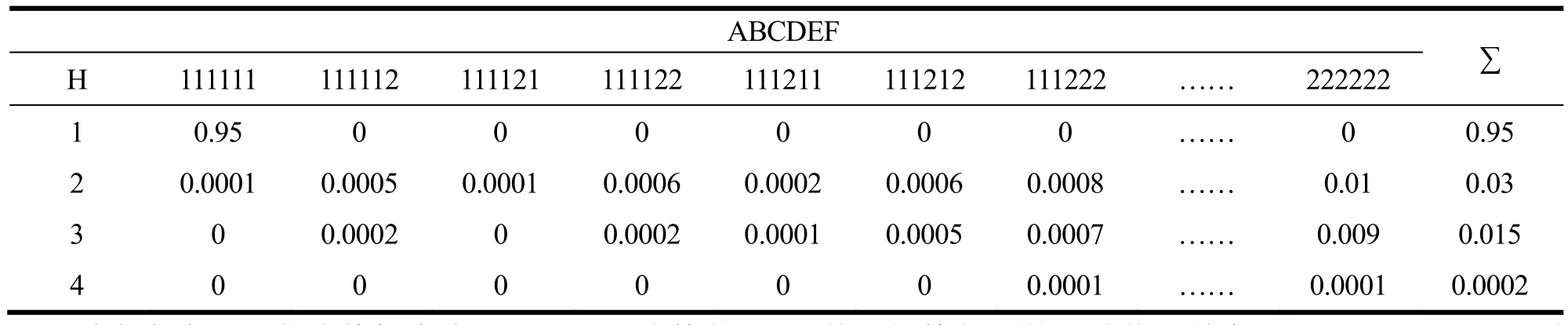
表7 白酒食品安全状况H的概率分布Table 7 Probability distribution of food safety status H
因此各危害因子的合格概率为P(Xi=1),不合格的概率为:

“白酒食品安全状况”的不合格概率,即评价指标的 阀 值 为 P(X21≠1)=P(H≠1)=P(H=2)+P(H=3)+P(H=4)=0.05。
利用matlab软件编程实现以上算法功能,建立网络模型,将训练集代入模型进行参数学习,可得白酒前 11个月每月总体情况的训练值和各节点不合格的概率值分别如图2、表8所示。

图2 前11个月每月总体情况的训练结果Fig.2 Training results of monthly overall status in the first 11 months
绝对误差越小,预测值越接近实际值,预测结果越精确。参数学习结果表明,贝叶斯网络模型得到的白酒每月的总体情况与实际的概率统计值的误差在0.0002~0.00263的范围内,各个危害因子的风险值与统计规律得到的风险值误差在 0.000011~0.000293的范围内,均低于0.05,属于合理的范围,因此贝叶斯模型预测的白酒总体状况接近实际值,危害因子的风险值是符合统计规律,精确度较高。
2 结果分析
2.1 有效性分析
将2016年12月份的测试样本集代入贝叶斯网络模型进行预测,可得12月白酒食品安全状态值和各个样本的不合格概率值。12月份白酒食品安全总体状况的预测值为0.0252,实际的状况值为0.02291,绝对误差为 0.00229,精确度较高。根据预警指标可知,12月份白酒食品安全总体状况的预测值和实际值处于“无警”状态,预测有效。12月各个样本不合格概率的实际值和预测值的绝对误差最大值、最小值分别为0.0687、0.0067,当误差范围为±0.05时,准确率为91.6%,准确度较高。因此,贝叶斯网络模型有效,能准确实现白酒食品安全风险预警。
2.2 稳定性分析
人工神经网络是食品安全预警研究常用的算法,但每次实验,神经网络的初始权值都是随机分配,以致运行结果不稳定。而贝叶斯网络结构和概率表一旦确定,每次运行结果不变。将实验数据分别代入三层BP神经网络、贝叶斯网络,实验重复 10次,第 12个月的预测结果如表9所示。BP神经网络相关参数设置如下:输入层、输出层分别为14、1个神经元;参照经验公式,运用试凑法得隐层节点神经元个数为4;因输出结果在0~1之间,则输出层、隐层传递函数分别为logsig、tansig;网络训练最小误差为0.0005,学习效率为0.05,训练次数为10000。
从表9的结果分析,准确率方面,神经网络和贝叶斯网络分别为91.2%、91.6%,两者相差仅0.4%,但是在10次重复实验中,神经网络的准确率有较大的浮动,贝叶斯的准确率保持不变。因此,相对于神经网络而言,贝叶斯网络模型运行结果更稳定。

表9 神经网络和贝叶斯网络的10次运行结果Table 9 10 running results of Neural Network and Bayesian Network
3 结论
结合白酒的检测数据,围绕金属污染物、农药残留,食品添加剂、品质指标、微生物污染和非食用物质6类危害因子,使用专家建模法构建贝叶斯网络模型的网络结构,运用最大似然估计算法进行参数学习,有机结合了先验知识和实验数据,准确、稳定地预测白酒食品安全状况,为白酒安全的防御和监测工作提供帮助,有利于白酒行业的发展,有益于人们的社会生产生活,有助于完善食品安全预警的技术方法。进一步的工作是结合改进的、以数据驱动的结构学习算法,根据数据的变动,及时调整网络结构和参数影响,发展成动态模型,更准确进行白酒食品安全预警,保障白酒食品安全。

