基于协同克里金的饮用水硝酸盐浓度预测研究

曹文翰，张 强，罗孝芹，时 晓，李红叶

(1.成都理工大学国家重点实验室，成都 610059；2.中国电建集团贵阳勘测设计研究院有限公司，贵阳 550081)

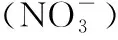
传统的水文地质调查方法需要对每户人家的饮用水点进行取样，这种方法成本高，在调查点数目众多且极为分散的情况下难度极大。地统计学可以通过少量样本点的硝酸盐浓度获得大尺度下硝酸盐浓度的分布情况[5]。其中克里金估值法相比于传统空间的确定性插值具有较高的可靠性，不仅可以进行插值，还可以定量计算误差和不确定度。协同克里金法把区域化变量之间的最佳估值方法从单一属性发展到了二个以上的协同区域化属性，充分考虑变量之间的统计相关性和空间关系，提高了主变量的估计精度[6,7]。

协同克里金法要求协变量和主变量之间存在较强的联系，变量之间联系越强模型就越稳定。因此，在众多变量之中找出同硝酸盐相关性最强的变量是进行协同克里金插值的基础。Distance模型可以计算观测值之间的距离大小即变量之间的相似或不相似程度的测度，但无法给出显著性P值；偏相关分析可以在多个变量存在时，控制其他多个变量的影响，计算两个变量的相关性[8,9]。本文借助Particle模型和Distance模型判断出相关性最强的变量并作为协变量，利用协同克里金方法反演研究区内硝酸盐的浓度，为后期的污染治理提供依据。

1 材料与方法

1.1 研究区域

研究区位于位于贵阳市东郊龙洞堡地区，研究区内居民分布松散，均是从山上引泉水下来生活饮用，饮用水源数目众多且分散。在易采样点地区收集24个水样点进行简分析后发现有超过42%的样品中硝酸盐含量超过美国环境保护署的最大污染物水平(EPA-MCL)指标值10 mg/L。因此查明该地区的硝酸盐分布情况显得尤为重要(见图1)。

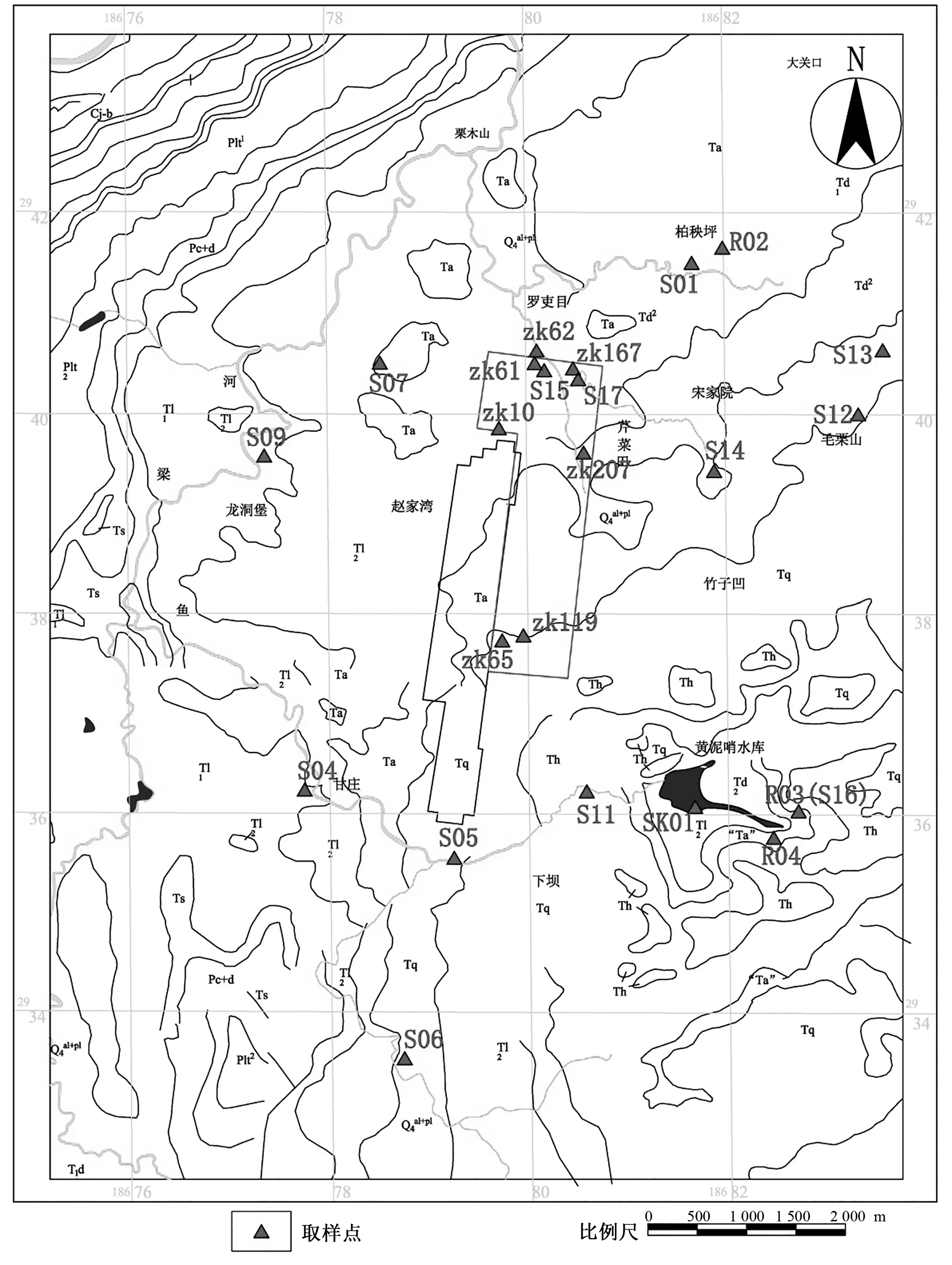
图1 地下水样采集点分布图Fig.1 The distribution of groundwater sampling points

1.2 相关性分析

偏相关分析在数理统计学中应用广泛，同传统的双变量分析相比，它能够在多个相互影响的变量之间剔除多余变量的影响，只分析两个变量之间的相关程度。该方法在处理高达12个变量的简分析数据时，拥有无可比拟的优势。

Distnce模型能将多个变量之间的相似程度用距离的大小表示出来，其结果在聚类分析、因子分析等多元分析方法之中应用广泛。在本文中选用欧几里得距离公式，它能够处理测量值相差悬殊的数据。

(1)

式中：i,j分别为数据的行列号；p为显著性值。

1.3 地统计学方法

变异函数是地统计学所特有的基本工具，它既能表征区间变量的空间变异结构，又能描述其随机性变化，是很多统计学计算的基础。样本的变异函数可用下式计算：

(2)

式中：N(h)为样点对的个数；Z为样本硝酸盐浓度；xi为样本点的位置。

对于多个变量，常需要计算协变量函数γij(h)。

Zi(xi′+h)] [Zj(xi′)-Zj(xi′+h)]

(3)

式中：N′(h)为分离距离h的Zi(x)和Zj(x)的样本对数。

如果变异函数表明变量具有空间相关性，克里金插值法就可以在变异函数理论及结构分析基础上，在有限区域内对区域化变量的取值进行无偏最优估计并通过分析有限的样本间的相关性，探索样本间的分布关系，并进行预测。协同克里金法把区域化变量的最佳估计方法从单一属性发展到二个以上的协同区域化属性，充分考虑变量之间的统计相关性和空间关系，提高了主变量的估计精度[10]。在二阶平稳假设条件下，其协方差公式为：

(4)

式中：Z1(xi)为主变量的测量值；Z2(xj)、λ1i、λ2j分别是Z1、Z2的权重，∑λ1j=1， ∑λ2j=1；m、n分别为主变量和协变量的测量点数量。

1.4 模型评价指标

模型的评价指标主要有标准平均值MS(Mean Standardized)以及均方根预测误差RMSS(Root Mean Square Standardized)。如果预测误差是无偏的，MS应接近于0。RMSS是用来考量误差的不确定性，以考察预测误差是否是最优的，RMSS越接近1精度越高，其公式如下：

(5)

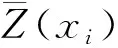
2 结果和分析

2.1 数据分析

表1 Distance模型分析结果表Tab.1 Expressions of distance model

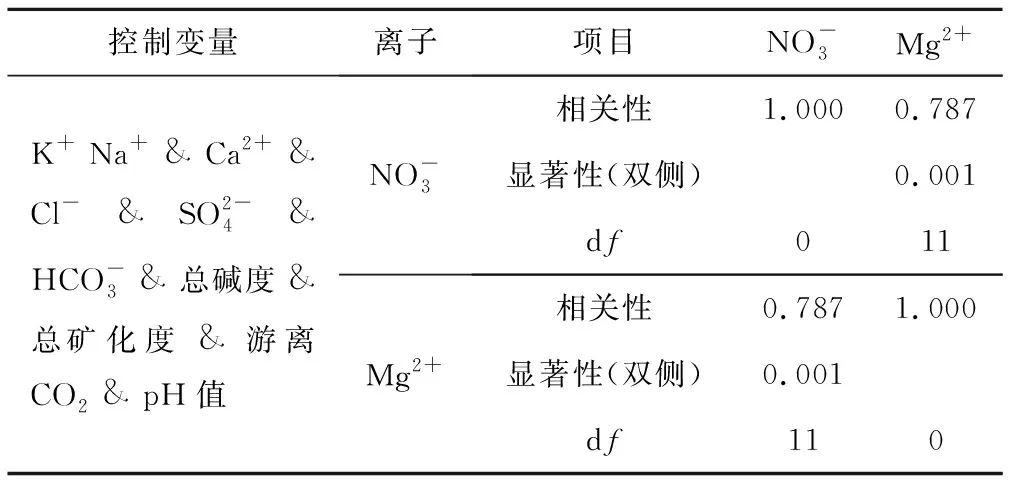
表2 偏相关分析结果表Tab.2 Expressions of particle model

2.2 半变异函数模型

克里金插值是在ArcGIS10.1的地统计分析模块(Geostatistical Analyst,GA模块)进行的。同其他的插值软件相比，ArcGIS最大的优点在于它会自动将一部分数据作为训练样本，另一部分数据作为检验样本以在交叉验证中保证结果的精度[11]。

克里金插值要求数据本身或变换后满足正态分布以及内蕴假设，因此在半变异函数建模之前，需对数据进行探索性分析(见图2)。发现数据进行log变换后会更加符合正态分布且需剔除全局趋势以排除变量的自相关性对模型精度产生的影响。

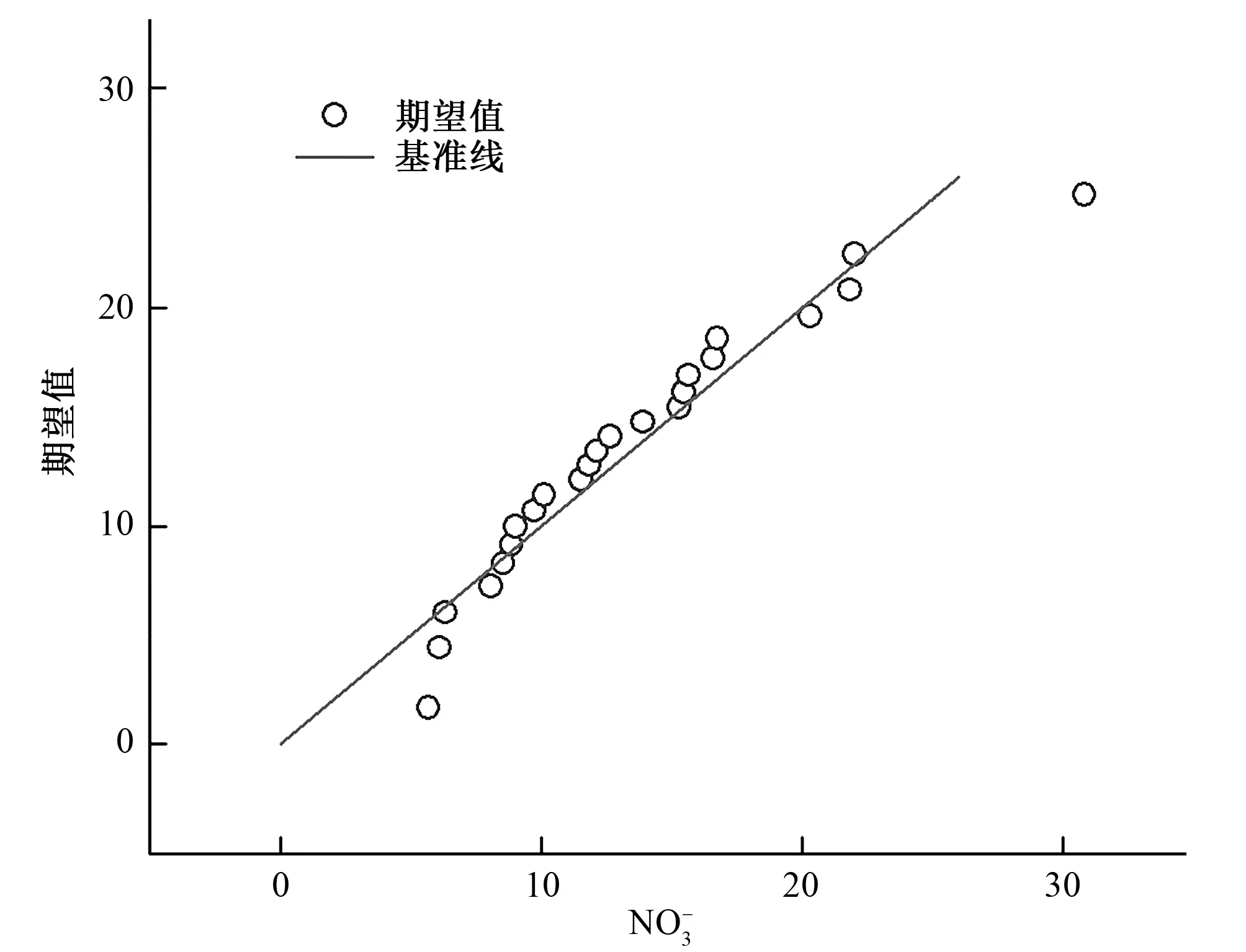
图2 正态Q～Q plot分布图Fig.2 Normal Q～Q plot of nitrate

地统计分析之后可以通过半变异函数建模来表示表面的非随机即确定性的组成部分，即从数据中剔除趋势后剩余的残差继续建模以表示表面局部变化的组成部分。块金值C0与基台值(C0+C)的比值表示可度量空间自相关的变异所占的比例，表明系统变量的空间自相关程度，比值越小，说明样本间的变异受随机变量影响越小，模型越稳健；模型的变程反映了简分析指标的空间连续性范围，变程以外的范围不存在相关性[12,13]。结果表明，协同克里金的块金值C0与基台值(C0+C)的比值为34.01%，优于协同克里金的块金值C0与基台值(C0+C)的比值58.04%，但两者均在25%～75%之间，表明系统具有中等的空间相关性，这与该地区地下水的补给来源较多且所取水样成分复杂有关。两个模型的变程均较大，这是由于该研究区域属于同一水文地质单元，空间相关的范围较大，同时也与研究区的空间尺度较大有关(见表3)。

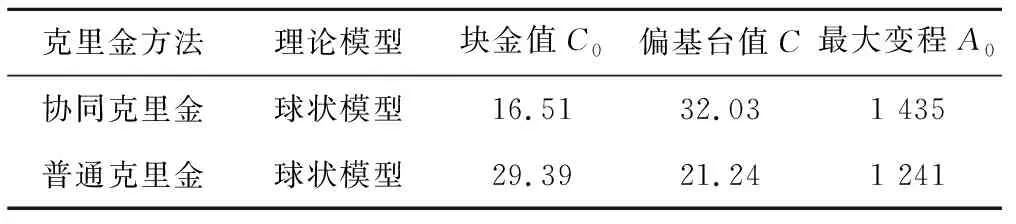
表3 半变异函数模型分析表Tab.3 Expression of semi-variogram model

2.3 预测结果的交叉论证

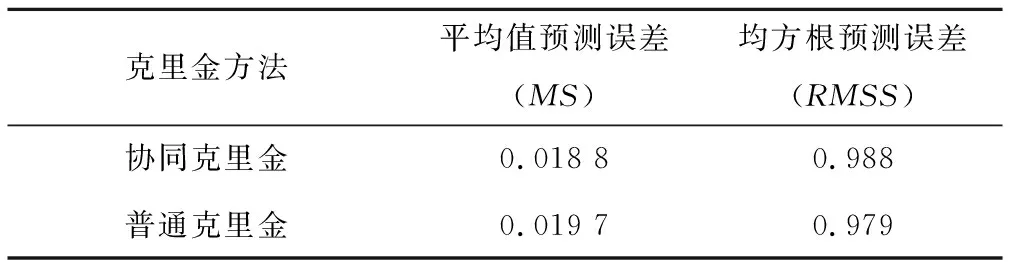
表4 交叉论证结果分析表Tab.4 Cross-validation results of model

2.4 研究区硝酸盐浓度分析

从硝酸盐浓度预测表面图图3可以看出，硝酸盐浓度整体上西比东高，南北比中间高并在最北端达到最高值22.01 mg/L。在区域内的敏感地带赵家湾人口聚集区和黄泥哨水库虽然硝酸盐浓度相对较低，主要原因为该地区使用氮肥较少，但浓度仍超过10 mg/L，可能会对居民身体健康造成不利影响。

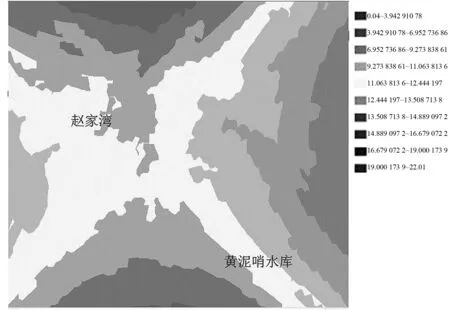
图浓度预测表面图Fig.3 The prediction surface map of Nitrate

3 结 语

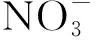
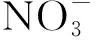
(2)对原始数据进行log变换并剔除趋势面后，进行半变异函数建模。模型的空间相关度均在25%～75%之间，表明系统具有中等的空间相关性，推测为地下水补给来源较多及所取水样成分复杂的原因。相比较而言，协同克里金模型比普通克里金模型更加稳健[C0/(C0+C)=34.01%，A0=1 435]。

(3)交叉论证结果表明，与普通克里金相比(MS=0.019 7,RMSS=0.979)，协同克里金的精度更高(MS=0.018 8,RMSS=0.988)，其所生成的硝酸盐浓度预测表面图能够为污染物的治理提供一定的指导意义。

参考文献：

[1] Galloway J N, Aber J D, Erisman J W, et al. The nitrogen cascade [J]. Bioscience, 2003,53(4):341-356.

[2] Galloway J N, Townsend A R, Erisman J W, et al. Transformation of the nitrogen cycle: recent trends, questions and potential solutions[J].Science, 2008,320(5878):889-892.

[3] Vitousek P M, Naylor R, Grews T, et al. Nutrient imbalances in agricutural development [J]. Science, 2009,324(5934):1 519-1 520.

[4] Nie S, Gao Y. Review of current status and research approaches to nitrogen pollution in farmlands[J]. Agriculture Sciences in China, 2009,8(7):843-849.

[5] 王仁铎，胡光道． 线性地质统计学[M]．北京: 地质出版社，1987．

[6] 刘治政,吴晓东,林洪孝. Kriging插值模型在地下水位监测网优化中的应用[J]. 人民长江,2010,41(9):14-17.

[7] 徐 驰,曾文治,黄介生,等. 基于高光谱与协同克里金的土壤耕作层含水率反演[J]. 农业工程学报,2014,30(13):94-103.

[8] 谢志英,刘 浩,唐新明. 北京市MODIS气溶胶光学厚度与PM10质量浓度的相关性分析[J]. 环境科学学报,2015,35(10):3 292-3 299.

[9] 成玉婷,李 鹏,徐国策,等. 丹江流域氢氧同位素变化特征[J]. 水土保持学报,2014,28(5):129-133.

[10] 李俊晓,李朝奎,殷智慧. 基于ArcGIS的克里金插值方法及其应用[J]. 测绘通报,2013,(9):87-90,97.

[11] Zhang Renduo. Applied geostatistics in environmental science[M]. Beijing: Science Press, 2005.

[12] Liu X, Wu J, Xu J. Characterizing the risk assessment of heavy metals and sampling uncertainty analysis in paddy field by geostatistics and GIS[J]. Environmental Pollution, 2006,141(2):257-264.

[13] Calzolari C, Ungaro F. Predicting shallow water table depth at regional scale from rainfall and soil data[J]. Journal of Hydrology, 2012,s414-415(2):374-387.