机器学习在径流预测中的应用研究

苏辉东，贾仰文，倪广恒，龚家国，曹雪健，张明曦，牛存稳，张 迪

(1. 清华大学水利水电工程系，北京 100084；2. 中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038)

0 引 言

近年来，大数据技术在全球发展迅猛，掀起了基于大数据的机器学习和人工智能的研究热潮，引起全球业界、学术界和各国政府的高度关注[1]。机器学习可以深度挖掘大数据的深度价值和内在联系，在各个领域、学科交叉中有着良好的应用[2,3]。机器学习，是一门研究怎样用计算机来模拟或实现人类学习活动的学科，它是人工智能中最具有智能特征的前沿研究领域之一，也是知识发现、数据挖掘等领域的重要基础[4,5]。例如：数据挖掘、计算机视觉、生物特征识别、搜索引擎、医学诊断、DNA序列测序、语音和手写识别、战略游戏和机器人运用[6]。机器学习可以应用于基于雷达图像的短期降水预报和径流预测，从而提升水文预报业务的效率，用大数据力量推动水文预报、径流预测的发展。

径流预测是水资源管理、调配和高效利用的基础。径流过程是一个高度复杂的非线性过程，传统的方法是采用水文模型进行预测。目前的水文模型存在很多的发展瓶颈，基于概念模型如Horton模型、Philip模型、Kostiakov模型、水箱模型、新安江模型等回归形式单一，公式表达式单一，无法得到很好的预测效果，难以完全适应所有的水文过程模拟[7]。基于物理的分布式或半分布式水文模型[8]问题如：第一，多尺度问题，如时间和空间尺度；第二，参数化问题，如参数的异质性等；第三是过程的复杂性，很多控制径流的过程不是简单的物理过程，而是化学或者生物过程以及人类活动等，例如蚯蚓和植物活动会在很大程度上影响入渗。

基于大数据的机器学习在径流预测具有操作简单的优点，可以忽略复杂的下垫面情况、水文过程，发展及其在应用科学领域的不断拓展，为认识、分析径流的变化规律提供了新的理论和方法。BP人工神经网络模型作为人工智能算法的代表，因其结构简单且具有良好的非线性映射能力，被广泛地应用于径流预测[9-11]。SVR算法出色的学习性能使得其在模式识别、回归估计、概率密度函数估计等方面都有应用[12,13]，在径流预测中也有很好的应用[14,18,19]。本文采用的对照的传统水文模型为THREW模型[15-17]，在中国的乌鲁木齐河流域[16]、美国的Blue River流域[17]和Sangmon流域[18]等得到了较好的应用。

本文采用SVR和BP人工神经网络两种机器学习的方法，与传统的分布式水文模型(THREW)进行比较，通过对比 效率系数和相对误差指标，对各种预测方法进行分析对比，相关研究有助于径流预测的发展。

1 研究方法

1.1 研究区概况

本次案例选择的是长江流域的子流域，位于湖北省宜昌市当阳市河溶镇，研究区地理区位如图1所示。流域出口控制断面为河溶镇水文站，地理坐标为东经111°56′，北纬30°36′，流域面积约200 km2。

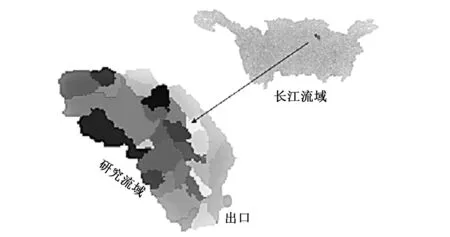
图1 研究流域地理位置及子流域划分图

1.2 模型介绍

(1)THREW模型。采用的水文模型为THREW 模型，这是一个分布式流域水文模型，主要应用于宏观尺度。田富强等对代表性单元流域(Representative Elementary Watershed，REW)进行了扩展和补充从而建立了THREW模型[13,19]。代表性流域单元(简称REW)是经过严格定义的子流域，也是模拟流域水文响应的基本单元。THREW 模型将代表性流域单元分为地表和地下2 层，其中对地下层进行进一步划分，成为2 个子区，地表层划分为6 个子区，能够反映植被、裸土、冰川、积雪等4 种典型下垫面类型。针对上述3 个级别的子系统，应用连续介质热力学守恒定律及均化方法，得到REW 尺度上的质量、动量和能量守恒的通用形式，具有较好的扩展性。在本文研究中，REW 的划分如图1 所示，共将全流域分为30个REW。该模型在长江流域的径流预测取得很好的效果。

(2)BP神经网络。BP神经网络[20-22]是一种按误差逆向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP神经网络能学习和存贮大量的输入-输出模式映射关系(见图2)。网络模型它的学习规则是使用最速下降法，通过反向传播不断调整网络的权值和阀值，使网络的误差平方和最小[23]。其中权值和阈值的调整公式如下：

(1)

式中：E为网络输出与实际输出样本之间的误差平方和；η为网络的学习速率即权值调整幅度；wij(t)为t时刻输入层第i神经元与隐含层第j神经元的连接权值；wij(t+1)为(t+1)时刻输入层第i神经元与隐含层第j神经元的连接权值；B为神经元的阈值，根据下标依次推其他符号的意义与权值。

图2 BP神经网络结构图

(3)SVR模型。采用SVR(Support Vector Regression)支持向量回归模型[24-26]，支持向量机回归与BP 神经网络类似，事先通过样本训练模型，然后对于训练好的模型预测，给定输入数据，就可以得到相应的预测输出。针对有限样本，一定程度上实现结构风险最小化、得到全局最优解，解决了在神经网络方法中无法避免的局部极值问题。针对给定的样本集{(xi,yi)|i=1,2,…,n} 其中xi为输入值，yi为预测值, 要求拟合的函数形式为：f(x)=wφ(x)+b。根据结构风险化最小化的原则，即要寻求最优回归超平面使：

(2)

式中：c为调节训练误差和模型复杂度之间折中的正则化常数；ε为不灵敏损失函数。

由支持向量机的回归问题转化为一个二次规划最优化问题：

(3)

SVR 用常分为线性和非线性拟合回归两类，对于非线性的情况，引入核函数即可，本文采用的核函数有：

(4)

本文采用SVR支持向量回归模型，内部采用不同的核函数及不同的惩罚因子，对2008-2012年当月及上月降雨量(二维)和当月径流量(一维)数据规律学习，模拟2013-2014年月径流量。

(4)Ns效率系数。

(5)

(5)相对偏差PB。

(6)

式中：Oi为观测值；Si为模拟值。

2 实例分析

2.1 THREW模型

采用传统分布式水文模型THREW，对河容镇流域进行模拟，本文将研究区划分为30个代表性单元子流域，建模中所使用的数字高程数据来自美国联邦地质调查局USGS，土壤资料来源于FAO，植被叶面积指数LAI根据归一化植被指数NDVI估算，水文气象数据分别由中国国家气象局和水利部水利信息中心提供。参数率定采用PEST自动调参软件和手动调参相结合的方法[27]。模型模拟期为2009年1月1日-2014年12月30日，其中2009年1月1日-2013年12月31日为模型率定期、2014年1月1日-2014年12月30日为验证期。

图3为THREW模型对河溶镇流域2009年1月1日-2014年12月30日日径流过程的模拟结果。从图3可以看出，THREW模型对流域径流量的模拟结果很好模拟了河溶镇流域。对丰水季节的径流模拟基本吻合，但是对枯水期的径流预估偏小。其Ns效率系数和相对偏差PB分别为0.503和16.6%(见表1)。从图3可以看出基于物理的THREW模型在枯水期的模拟偏小，在洪水期的径流预测还可以。从Ns效率系数来看，THREW模型预估径流是比较准确的，但是相对偏差PB有点偏大。总体来看，基于物理的分布式水文模型THREW，对河溶镇流域的径流过程拟合预报精度表现较好，从而说明改进的集合径流预报方法在汉江上游有着较强的应用价值。

图3 基于THREW模型模拟的径流结果

2.2 BP神经网络

本文BP人工神经网络实例选取河溶镇流域2009年1月1日-2013年12月30日的日降水和日径流数据，其中2008年1月-2013年12月的数据作为学习训练样本，2014年1月1日-12月30日为预测检验样本。模型的输入采用当日径流量与前天降水量(二维)作为输入数据，输出数据为当日径流量。

图4为BP人工神经网络模型对河溶镇流域2009年1月1日-2014年12月30日日径流过程的模拟结果。从模拟结果来看，模拟结果的Ns效率系数为0.463，相对偏差PB为2.3%。影响Ns效率系数的主要因素是对丰水期的大径流量预测偏差较大，甚至出现模拟失真的现象，但是对其他时期的预测是高度的准确，这也表明BP人工神经网络模型很难解决局部极值问题。总的来说，如果可以克服洪水期的预测失真问题，BP人工神经网络模型的模拟还是相当可信的。

图4 基于BP神经网络的径流模拟结果

2.3 SVR模型

本文SVR实例选取河溶镇流域2009年1月-2014年12月的月降水和月径流数据，其中没有学习训练样本，都为预测检验样本，SVR本身自带正交最小二乘优选，不需要进行样本训练。模型的输入采用当日径流量与前天降水量(二维)作为输入数据，输出数据为当日径流量。内部采用径向基核函数。

图5为基于SVR算法对河溶镇流域2009年1月-2014年12月月径流过程的模拟结果。

图5 基于SVR学习方法的模拟结果

从图5 可以看出，径向基核函数SVR的模拟结果在一定程度上解决了局部极值问题。在模拟效果有很大的提高，优于TREW模型和BP神经网络模型，得到全局最优解。但是其还是存在一定的最大洪峰预测偏小的状况，这在一定程度上使得影响Ns效率系数依旧偏低，但是这对其他的流量模拟相当可信。相对于TREW模型和BP神经网络模型。

2.4 结果对比分析

从数据结构来比较，TREW模型是综合气象数据、径流数据、土壤、下垫面、高程数据以及分析水文过程来预测径流，其数据来源分析复杂。相对而言机器学习需要的数据简单得多，如SVR与BP人工神经网络输入数据为当日径流量与前天降水量(二维)作为输入数据，输出数据为当日径流量。

为了比较3种径流预测方法的效果，本文采用Ns效率系数和相对误差PB作为比较指标，其结果如表1所示。

表1 3种方法预测效果对比结构

TREW模型模拟效果好，Ns效率系数为0.503，但是其相对偏差较大。BP神经网络拟综合效果较差其Ns效率系数为0.463，但是其相对偏差小，为2.3%。说明其有很好的逼近非线性映射的能力，但是局部极值等模拟失真，如实测值的极大值的峰值无法预测出来，这会影响BP神经网络在径流预测中的应用的效果。SVR预测径流比较而言最好，在低径流阶段模拟准确，对局部最大洪峰流量也模拟较准，但是也存在一定偏差。

不同的预测方法往往有着不同的预测结果，不同的预测方法挖掘不同的有用信息，不同模型的预测结果通常具有互补性，其预测精度也各有悬殊，而没有一种适用于所有预测的通用方法。一种预测方法都有其适用性和局限性，应依据实际问题选择适当的模型与方法。本次采用的传统分布式水文模型，模拟效果较好，具有清晰的物理过程，能明白其中的水文机理，但是数据要求较多，操作复杂。本次采用的两种机械学习方法，都较好的模实现了对径流的预测。泛化能力较好，即具有将学习成果应用于新知识的能力。本次采用的SVR和BP神经网络模拟案例中，除了洪水预报不准外，日径流量具有较好的预测。但是同时也存在以下缺点：对数据依赖较大，样本依赖性大，如果数据样本容量再大，预测的结果可能会更理想。另外机器学习预测径流的方法是一个纯黑箱模型，现实意义不清楚，难以对流域本身变化引起径流的变化进行预测。另外，在本次预测中SVR的综合效果比BP较好，其两项指标Ns效率系数和相对偏差PB都优于BP，在一定程度上克服了洪峰径流的预测失真问题。

3 结 语

本文用SVR和BP人工神经网络两种机器学习的方法，对比了传统的分布式水文模型(THREW)，采用Ns效率系数和相对误差PB指标进行分析。结果显示，本次采用的传统分布式水文模型THREW，模拟效果好，Ns效率系数为0.503，具有清晰的物理过程和水文机理，但是数据要求较多，操作复杂。本次采用的两种机械学习方法，都较好的模实现了对径流的预测。泛化能力较好，即具有将学习成果应用于新知识的能力。本次采用的BP神经网络模拟案例中，除了洪水预报不准外，日径流量具有较好的预测，SVR对极大洪峰流量预测准确度有所提高。但是同时也存在以下缺点：对数据依赖较大，样本依赖性大，如果数据样本容量再大，预测的结果可能会更理想。本次模拟结果显示SVR优于TREW模型和BP神经网络模拟结果。

□

参考文献：

[1] 黄宜华. 大数据机器学习系统研究进展[J]. 大数据, 2015,1(1):28-47.

[2] 雷晓云, 张丽霞, 梁新平. 基于MATLAB工具箱的BP神经网络年径流量预测模型研究----以塔城地区乌拉斯台河为例[J]. 水文, 2008,28(1):43-46.

[3] 张利平, 王德智, 夏 军,等. 相空间神经网络模型及其在水文预测中的应用[J]. 水电能源科学, 2004,22(1):5-8.

[4] 王雪松. 机器学习理论、方法及应用[M]. 北京：科学出版社，2009.

[5] 杨淑莹, 张 桦. 模式识别与智能计算:MATLAB技术实现[M]. 北京：电子工业出版社, 2015.

[6] 李凡长. 机器学习理论及应用[M]. 合肥：中国科学技术大学出版社，2009.

[7] 刘佩瑶, 郝振纯, 王国庆,等. 新安江模型和改进BP神经网络模型在闽江水文预报中的应用[J]. 水资源与水工程学报, 2017,28(1):40-44.

[8] 贾仰文, 王 浩, 倪广恒, 等. 分布式流域水文模型原理与实践[M]. 北京：中国水利水电出版社, 2005.

[9] 徐中民, 蓝永超. 人工神经网络方法在径流预报中的应用[J]. 冰川冻土, 2000,22(4):372-375.

[10] 蓝永超, 康尔泗, 徐中民,等. B-P神经网络在径流长期预测中的应用[J]. 中国沙漠, 2001,21(1):97-100.

[11] H Raman, N Sunilkumar. Multivariate modelling of water resources time series using artificial neural networks[J]. International Association of Scientific Hydrology Bulletin, 1995,40(2):145-163.

[12] Gui G Q. Face recognition using support vector machines[J]. Computer Science, 2003,30(4):11-15.

[13] Hearst M A, Dumais S T, Osuna E, et al. Support vector machines[J]. IEEE Intelligent Systems & Their Applications, 2002,13(4):18-28.

[14] 王景雷, 吴景社, 孙景生,等. 支持向量机在地下水位预报中的应用研究[J]. 水利学报, 2003,(5):122-128.

[15] 田富强, 胡和平, 雷志栋. 基于代表性单元流域的水文模拟理论与方法[DB/OL]. http:∥www.paper.edu.cn, 2005.

[16] Mou L, Tian F, Hu H, et al. Extension of the representative elementary watershed approach for cold regions: constitutive relationships and an application[J]. Hydrology & Earth System Sciences Discussions, 2007,4(5):565-585.

[17] Tian F, Li H, Sivapalan M. Model diagnostic analysis of seasonal switching of runoff generation mechanisms in the Blue River basin, Oklahoma[J]. Journal of Hydrology, 2012,s418-419(4):136-149.

[18] Liu D F, Tian F Q, Hu H P, et al. Sediment simulation at Upper Sangamon River basin using the THREW model[C]∥ Hydrological Modelling and Integrated Water Resources Management in Ungauged Mountainous Watersheds. Proceedings of A Symposium Held at Chengdu, China, 2009.

[19] TIAN Fuqiang, HU Heping, LEI Zhindong, et al. Extension of the representative elementary watershed approach fof cold regions via explicit treatment of energy related processes[J]. Hydrology and Earth System Sciences, 2006,10(5):619-644.

[20] 崔东文. 多隐层BP神经网络模型在径流预测中的应用[J]. 水文, 2013,33(1):68-73.

[21] 杨 洪. 改进 BP 神经网络集成模型在径流预测中的应用[J]. 水资源与水工程学报, 2014,(3):213-219.

[22] 聂 敏, 刘志辉, 刘 洋,等. 基于PCA和BP神经网络的径流预测[J]. 中国沙漠, 2016,36(4):1 144-1 152.

[23] 季 云. BP算法及其应用实例[J]. 中国新技术新产品, 2010,(9):29.

[24] 明 琦, 刘俊萍. 兰州站径流支持向量机预测[J]. 水力发电学报, 2010,29(4):32-38.

[25] 郭 俊, 周建中, 张勇传,等. 基于改进支持向量机回归的日径流预测模型[J]. 水力发电, 2010,36(3):12-15.

[26] 卢 敏, 张展羽. 径流预测的支持向量机应用研究[J]. 中国农村水利水电, 2006,(2):47-49.

[27] Doherty J. PEST: a unique computer program for model-independent parameter optimisation[Z]. Australia: 1994.