基于小波支持向量机特征分类的日径流组合预测----以宜昌三峡水库为例

黄景光，吴 巍，程璐瑶，于 楠,3，陈 波,3

(1.三峡大学电气与新能源学院，湖北 宜昌 443002；2. 三峡大学 梯级水电站运行与控制湖北省重点实验室，湖北 宜昌 443002；3. 三峡大学 新能源微电网湖北省协同创新中心，湖北 宜昌 443002)

1 研究背景

河流径流作为水文学一个重要的组成部分，主导着水文系统的变化，其受天文、气象、地理等多因素影响，具有很强随机性、非线性、突变性等复杂特性。而径流预测是制定合理的水库运行策略的重要依据，直接影响水库防洪设施设置、发电运行方式，通过合理的径流预测可以大大提高工程综合效益[1-4]。近年来，随着计算机和数学方法的发展，以历史径流为基础的径流预测方法越来越多,其中ANN与SVM以及其组合方法成为目前研究热点。根据水文特点，径流预测通常采用BP神经网络模型，仅需三层结构就能满足一般水文预测需求，泛化和容错能力强，但收敛速度慢，容易陷入局部最优[5-7]。由Vapnik等根据VC维理论与结构风险最小原理提出的SVM能够很好地解决收敛速度慢、易陷入局部最优等缺点，对于小样本、高维度数据同样有良好的处理能力[8]。

ANN和SVM已经应用于多个水文预测工程[9-13]，但径流与多种自然因素具有强相关性，其本身非线性强，时间空间尺度上变化复杂，利用单一数学模型预测困难，误差较大。水文序列含有多种频率成分，不同频率成分对预测精度有着一定影响，小波分析能对水文序列“由粗到细”展示其变化规律，同时能够获得不同频率序列。因此，利用小波分析与其他数学方法建立耦合模型为径流预测提供了一种新途径。黄巧玲等[14]将小波分析与支持向量机结合建立WSVR回归模型提高了径流预测精度。Patil S K等[15]研究了多层感知器和模糊神经网络对径流预测精度与稳定性的影响。纪昌明等[16]将小波分解和投影寻踪法建立耦合模型，提高了预测精度也增加稳定性。王秀杰等[17]将小波分解的高低频分量用ARMA模型预测，重构后预测合格率提升至90%。

以上文献均以单一方法对径流序列进行预测，未考虑径流序列随机程度对于预测方法的选择性。本文将SVM分类器与小波分析技术组合提出一种基于径流特征和小波高低频能量谱分类的ARMA、ANN组合预测方法。在保证ARMA模型预测精度的前提上进行特征分类，之后通过小波分解和SVM对预测周期内不同类型序列采用不同预测方法预测，并对重构后的径流预测精度进行分析。在风电、光伏组合预测中，该方法已被证实能够极大地提高预测精度[18,19]。本文以2013-2017年宜昌站径流为例，验证了本文预测方法的可行性和有效性。

2 径流组合预测模型原理

河川径流受极端天气、气候变暖、水利工程等影响，在一个水文年中汛期径流有明显增长趋势，使径流曲线呈强非线性，在非汛期变化平缓，在一些研究中通常对汛期和非汛期采用不同方法预测[14]，但这样通常忽略了汛期中“平稳型”径流和非汛期的“突变型”径流(主要受极端天气影响[2])，为此需对径流序列进行自适应分类，避免误分类情况发生。

在多数研究中，对于短时间变化较大的序列常常利用ANN进行预测，其容错效果好，预测误差较小；趋于平稳的序列则采用ARMA模型进行预测，其较于ANN在同等的预测精度下，计算量较小。因此对于某一径流序列，在预测期内将序列分为“平稳”和“突变”两种类型，“平稳型”序列使用ARMA模型预测，“突变型”序列使用ANN预测[20]，具体分类方法见3.2节。本文则通过小波分解与SVM建立组合分类器来完成这一过程。

基于以上原理设计的组合预测模型，其工作步骤如图1所示。首先，通过3.1节方法对原始径流序列提取高频系数能量谱，通过3.2节方法确定序列特征类型，再将两者作为样本标记和特征信息输入至SVM分类器中来预测预测期内序列的特征类型，实际中，预测期内的径流序列类型未知，但是可以通过历史径流数据对下一时段的序列类型进行预测，SVM具有根据原特征信息对未来特征预测的能力，其分类预测方法具体见3.3节。

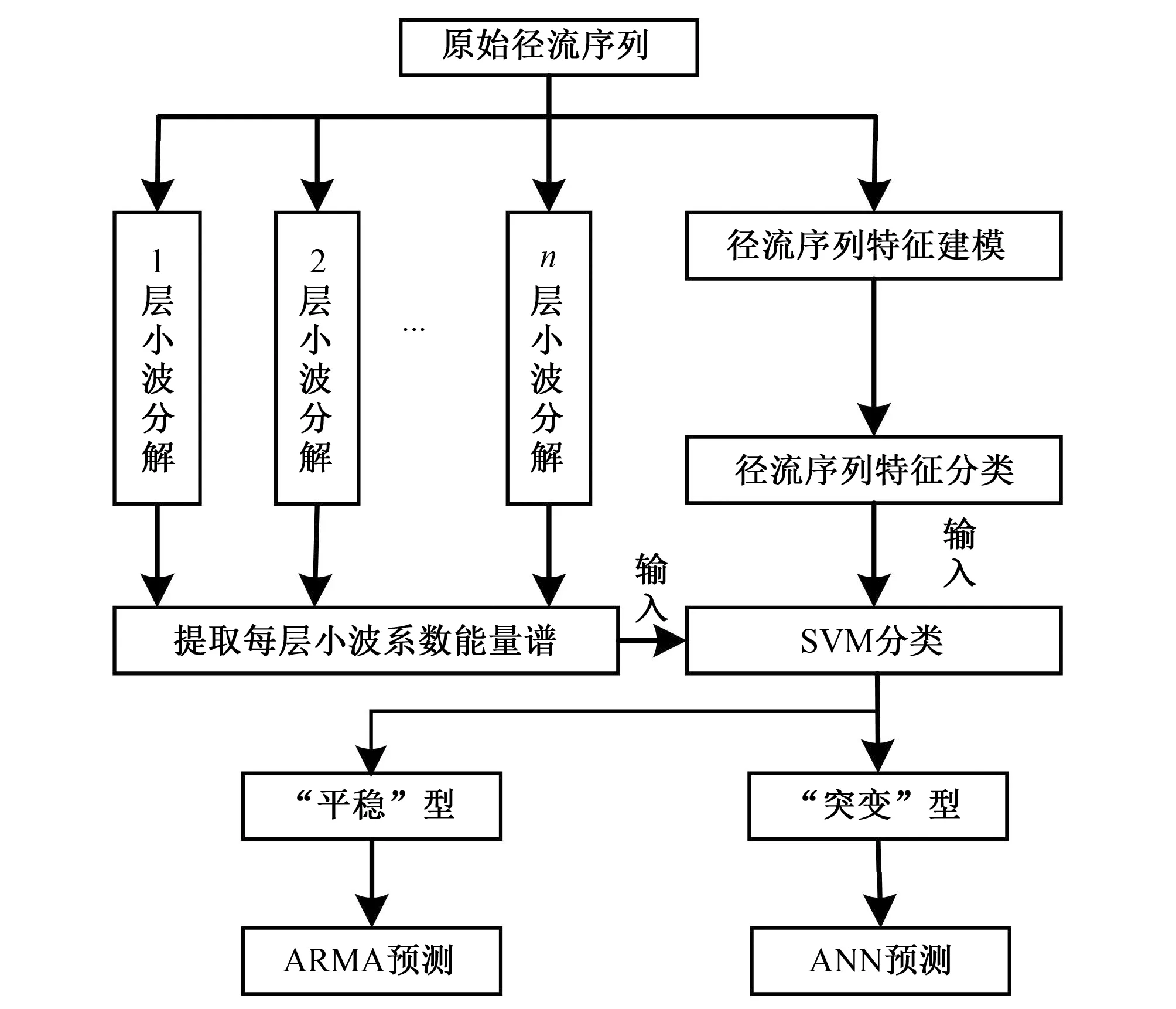
图1 组合预测流程Fig.1 Combination forecasting process

本文分别选取汛期与非汛期径流进行预测效果对比，将原始径流前95%作为训练集，后5%作为预测集，前95%的序列进行小波分解得到小波系数的能量谱，之后将能量谱输入至SVM分类器预测后5%的径流曲线类型，最后根据预测期内序列类型的不同选用对应的预测方法预测。

3 研究方法

3.1 径流序列小波变换分解

对于f(x)满足f(x)∈L2(R)，L2(R)为R平方上可积函数构成的函数空间，Ψ(t)为一个基小波或母小波，连续小波变换为：

(1)

对于离散信号f(nΔt)，WΨf(a,b)变换形式为：

(2)

式中：Δt为采样时间间隔；n为样本序列，n=1,2,…,N；N为样本容量。

在实际工程中，一般采用离散的时间序列，对于任意原始序列，可以使用Mallet算法进行分解。Mallet算法是一种快速小波方法，分为分解和重构两类算法。

Mallet快速分解算法为：

(3)

Mallet重构算法为：

cj=Hcj+1+Gdj+1j=J-1,J-2,…,0

(4)

式中：H、G分别为高低通滤波器；J为尺度数。

通过式(3)可以将一原始序列分解为aJ和d1,d2,…,dJ，aJ为原始信号的近似部分，dJ为原始信号的细节部分。

本文利用Mallet算法采用正交不对称db4小波包函数对径流序列进行2层分解来获取其近似和细节信号。分解尺度虽对预测结果影响不大，但尺度过大或过小会导致数据提取不完整，影响模型性能，因此分解尺度需在预测时进行测试再逐一比较进行选取。现以长江宜昌站2016年实测日径流作为样本进行分析。

图2为径流序列经小波分解后的能量谱图，从图2可以看出在中间时段径流序列变化频率和幅度较大，序列产生“突变”，对应时段的高频信号能量谱有着明显的陡增现象，该现象能够很好地反映径流的变化情况。因此，本文将径流序列的能量谱作为SVM分类器的训练样本特征以及训练完成后的输入变量。

图2 径流序列及小波分解能量谱Fig.2 Runoff series and wavelet decomposition energy spectrum

3.2 径流序列特征分类

径流序列可以依据在一段时间内，其突变陡度(即导函数)是否存在过零点，以及斜率变化范围进行划分。若在这段时间内，曲线导函数不存在过零点，或斜率变换范围不大，则认为这段时间径流序列属于“平稳”型，反之则属于“突变”型。径流特征分类的判决条件如下：

(5)

式中：sgn为符号函数；sgn(smax)、sgn(smin)分别为径流曲线导函数最大最小值；K为曲线类型，K=1，则曲线类型为“平稳型”，此段曲线采用ARMA模型进行预测，K=0，则为“突变型”，采用BP神经网络进行预测。d1、d2作为曲线类型的判别参数，其物理意义为径流序列变化程度与周围环境对应关系。

同时，d1、d2应满足ARMA在预测过程中平均误差εave尽量小于20%，即：

(6)

式中：εave为ARMA平均预测误差；εi、Ki分别为第i个预测周期的误差和序列类型；n为本次预测总周期数。

对于式(6)采用遗传算法求解，其适应度函数为：

(7)

该特征类型作为SVM训练样本标记，不会因为遗传算法求解时长而影响预测精度。对于d1、d2的数值选取，首先根据式(5)采用ARMA进行预测，对预测误差绝对值求和后，取平均得到式(6)，最后通过求解式(7)，可得到d1、d2。

3.3 SVM分类

利用历史径流数据建立SVM分类器，其具体结构如图3所示。首先，对一年中各日径流利用3.1节方法进行小波分解，并将小波分解系数能量谱作为SVM分类训练特征；之后，采用3.2节方法对各日径流序列进行分类，各分类类型作为SVM训练样本标记。进行训练后，即可作为本模型所需的SVM分类器。

图3 SVM分类器建立Fig.3 Establishment of SVM classifier

利用2016年1-6月和9-12月径流数据对SVM分类器进行训练，为提高预测精度，需对输入数据进行对数化和归一化处理。图4为SVM分类训练结果。

图4 支持向量机分类Fig.4 Classification of support vector machine

利用2016年7月和8月径流数据作为测试集来验证SVM分类器的预测分类精度，分类号“0”和“1”分别代表“突变型”和“平稳型”，验证结果见表1。从表1可知，SVM在16至19时段发生误判，分类准确度为87%以上，说明SVM分类能通过小波能量谱对一定时序内的径流曲线进行较为准确的分类，同时SVM分类结果将作为选取不同径流序列类型预测方法的依据。

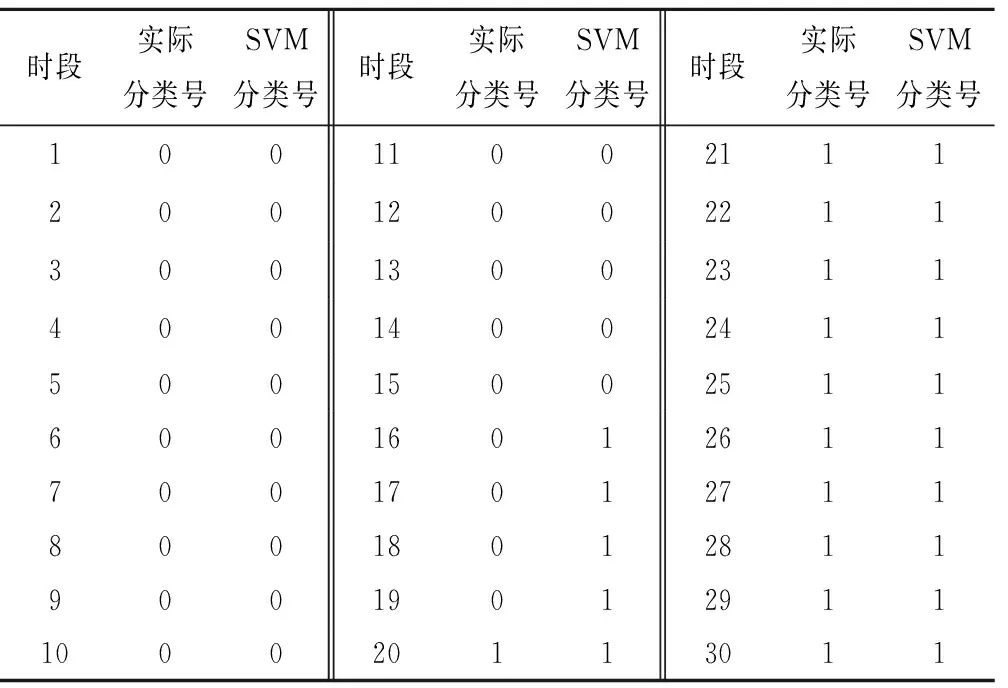
表1 SVM判定分类结果Tab.1 SVM determines classification results

4 径流预测方法

4.1 ARMA模型

ARMA模型由自回归模型(AR)和滑动平均模型(MA)混合构成,其一般形式为：xt-φ1xt-1-K-φpxt-p=at-θ1at-1-K-θqat-q。用Bk表示k步推移算子，即Bkxt=xt-k，Bkat=at-k，Bkc=c，c为常数。并令：

φ(B)=1-φ1B-φ2B2-K-φpBp

(8)

θ(B)=1-θ1B-θ2B2-K-θpBp

(9)

则可简记为：φ(B)xt=θ(B)at。该模型通常以ARMA(p,q)表示，计算公式如下：

(10)

式中：aj和p分别为AR的系数和阶数；bj和q分别为MA的系数和阶数；εt为滞后因子。

ARMA适用于当前时序系统变化规律在未来的变化趋势不变或变化较小的情况，在式(5)对径流序列进行判定，“平稳型”径流在某一时序内具有单调递增或递减性质，且有较小的斜率变化，同时在递增或递减时幅度有一定变化，说明径流具有随机波动性。因此，该情况适合使用ARMA进行时序分析，其一般步骤如图5所示。

图5 ARMA预测流程Fig.5 ARMA prediction process

4.2 ANN模型

对于式(5)判定的“突变型”径流序列，在某一时序内变化规律不明显，无单调情况或斜率变化范围较大，此时使用ARMA进行预测误差较大，而BP神经网络作为使用最为广泛的神经网络模型之一，其对强非线性数据具有高精度拟合的优点[21]，使用BP神经网络对“突变型”径流序列预测效果更好。

以3.1节方法对“突变型”径流采用db4小波分解成近似和细节信号，近似信号可看作在一定序列内原始信号的大致变化规律，细节信号可看作对近似信号的随机扰动。本文通过对2层小波分解的低频和高频信号采用BP神经网络进行预测，后对预测信号进行小波重构获得时域预测径流，会比直接对时域径流预测精度高，其一般预测步骤如图6所示。

图6 BP神经网络预测流程Fig.6 BP neural network prediction process

4.3 模型效果评价

为更明确判别本文模型预测精度和有效性，本文选用平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、均方根误差(Root Mean Square Error,RMSE)、希尔不等式系数(Theil Inequality Coefficient,TIC)[22,23]对模型分析，其具体公式如下：

(11)

(12)

(13)

5 算例结果分析

考虑数据的时效性本文采用长江宜昌站2013-2017年三峡入库径流作为研究数据(2017年数据为1-11月)，其中2016年6、7月和2017年10、11月径流作为预测数据，以对比丰枯水期预测差异。通过Matlab 2014a与Libsvm-3.22工具箱来实现本文预测方法，并与ANN和ARMA单一预测模型作比较。小波分解将径流时间序列分解为{a2(t),d2(t),d1(t)}高低频序列，如图7所示。

图7 小波系数谱Fig.7 Wavelet coefficient spectrum

从图7可看出2013-2017年三峡入库径流规律，丰水期为6-10月，枯水期为11-2月，小波分解的低频系数与原始序列具有强相关性，高频信号与原始序列相关性很差，在预测过程中高频信号可视为无效序列不进行预测，但本文也采用BP神经网络对高频信号进行预测以提高预测精度，同时，如3.1节所述，高频信号能量谱(见图2)也可以作为SVM分类器的特征样本。

本文根据SBC准则采用以5阶自回归-3阶滑动平均系数的ARMA(5，3)作为ARMA预测模型。对于BP神经网络，采用个输入层节点数6，隐含层数10，输出层数1的6-10-1三层结构模型，训练算法为Bayesian-Regularization(该训练算法虽比Levenberg-Marquardt训练时间长，但预测精度更高，且由于日径流预测时间较长，训练时间可以忽略不计)。经3种方法预测后，结果如图8～图10所示。

图8 ARMA预测结果Fig.8 Prediction result of ARMA

图9 BP神经网络预测结果Fig.9 Prediction result of BP-ANN

从图8和图9可以看出，ARMA和ANN模型预测效果较为接近，为更好地评价模型预测的有效性，采用4.3节的评价函数模型误差进行统计，ARMA模型总拟合度误差MAPE=6.51%，RMSE=2 153.9 ，TIC=7.51%；ANN模型总拟合度误差MAPE=6.19%，RMSE=1770.5 ，TIC=5.87%。由于径流序列随机性较强，ARMA对“突变型”序列预测误差较大，因此总拟合误差大于ANN拟合误差，ANN虽对“突变型”序列预测效果优于ARMA模型，但ANN模型需要不断进行训练寻求最优预测值，预测时间较长。

从图10可看出本文模型拟合度远高于ARMA和ANN模型，总拟合度误差MAPE=1.30%，RMSE=276.4 ，TIC=0.91%。通过对径流序列进行小波分解和SVM特征分类，“平稳型”序列采用ARMA模型预测，“突变型”序列采用ANN模型预测，比单一模型预测精度更高。

图10 小波-SVM特征分类组合预测模型Fig.10 Combination forecasting model based on wavelet -SVM feature classification

2016年6、7月为三峡水库丰水期，从图11看出其径流变化幅度较大，每隔2～3 d，曲线斜率在正负之间发生转变，这是作为分类标记的重要一部分信息，其预测后评价模型结果见表2。结合图表信息可以看出，ARMA预测序列波动明显，输出不稳定，预测误差最大。BP神经网络相对于“突变”序列具有强容错性，其预测误差比ARMA平均少4%，但本文模型通过小波分解过滤掉细节信号，增加了近似信号的平滑程度，使特征分类准确性提高，其预测误差又比BP模型平均提高6%。

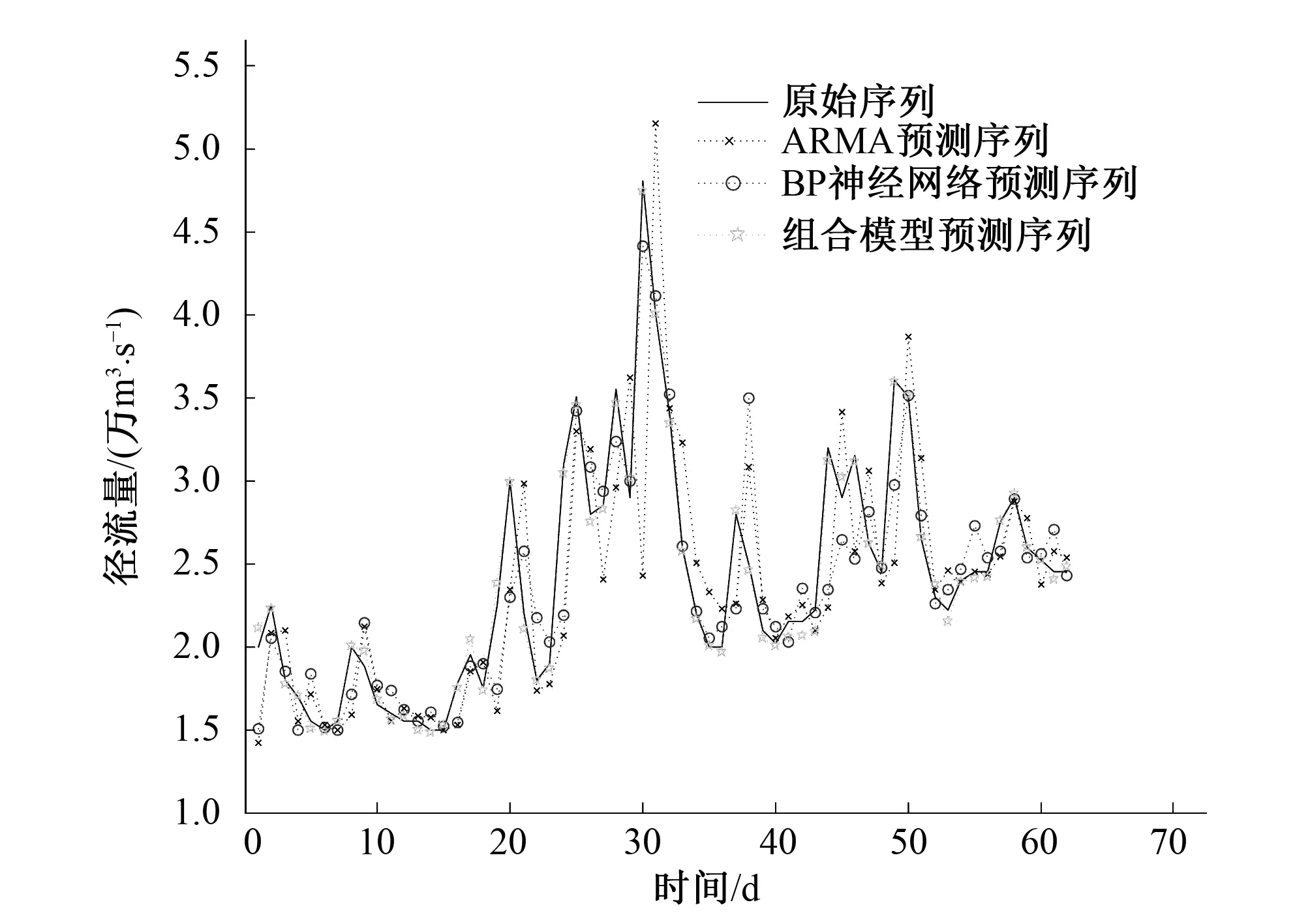
图11 2016年6、7月预测径流序列Fig.11 Prediction of runoff series in June and July 2016

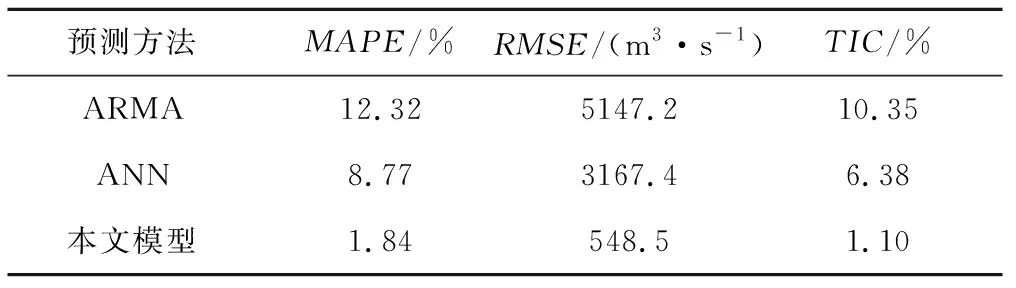
预测方法MAPE/%RMSE/(m3·s-1)TIC/%ARMA12.325147.210.35ANN8.773167.46.38本文模型1.84548.51.10

2017年10、11月为三峡水库枯水期，径流序列斜率逐渐平稳，变化幅度降低(见图12)。从12月预测径流序列可以看出本文模型预测序列与原始序列最为接近，评价模型统计结果见表3。由于径流序列变化程度降低，相比于丰水期，ARMA预测精度约提高3.5%，与BP神经网络预测精度只相差0.9%，但本文预测模型在所有评价指标仍远优于前两种模型，相对于ARMA和ANN模型，本文模型预测MAPE平均减少6%，RMSE减少1 900 ，TIC减少5.5%，且预测序列波动最为平滑，模型预测稳定性最高。

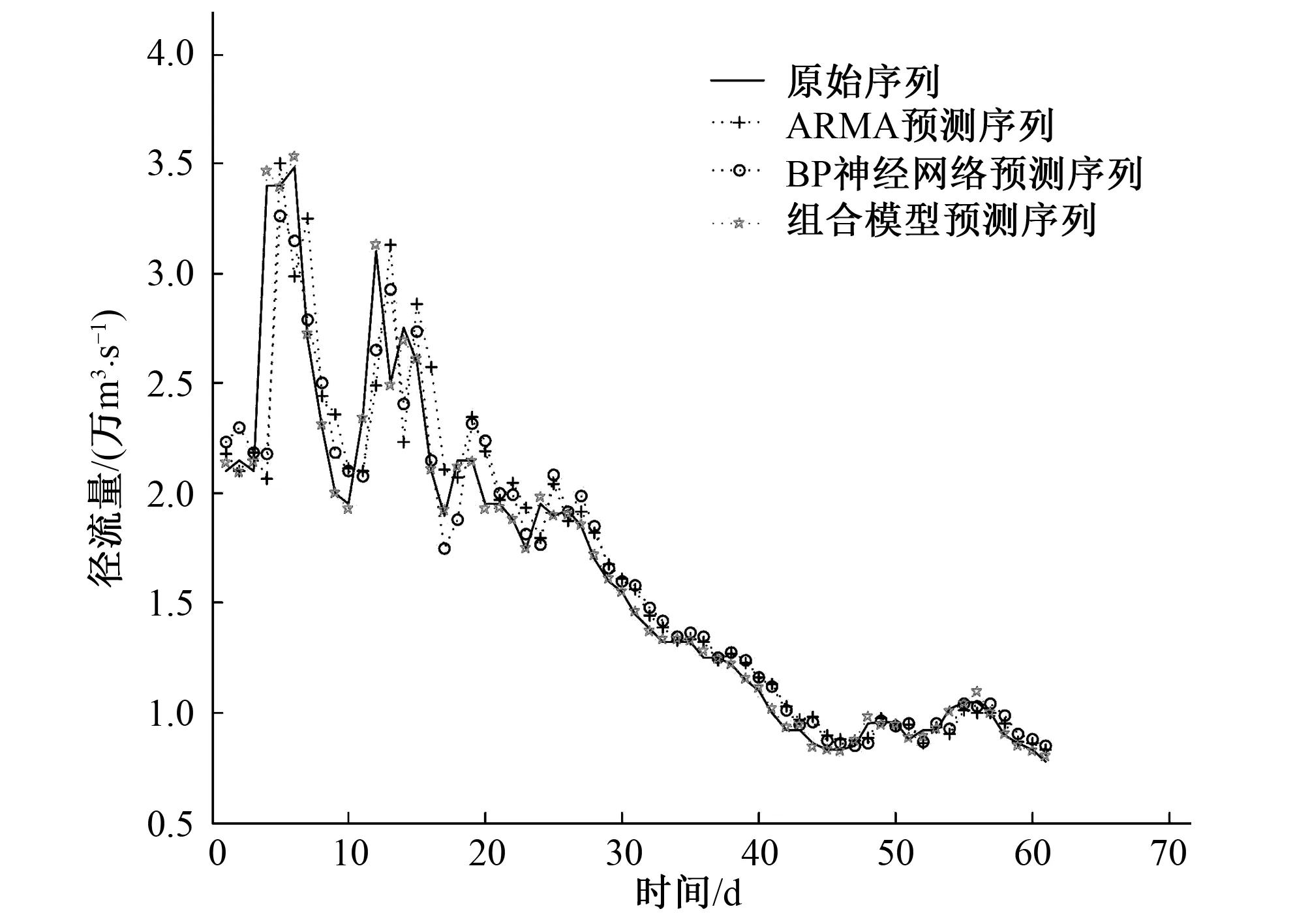
图12 2017年10、11月预测径流序列Fig.12 Prediction of runoff series in October and November 2017

预测方法MAPE/%RMSE/(m3·s-1)TIC/%ARMA7.962661.57.45ANN7.072166.06.11本文模型1.12225.70.63

6 结 语

本文通过构建径流特征样本模型、利用小波分解提取小波系数能量谱作为样本标记，采用SVM分类器将径流序列分为“平稳型”和“突变型”，根据不同径流序列类型分别采样ARMA和ANN模型预测，该模型显著特点是利用小波分析的多尺度分解能力和SVM泛化分类的特点，实现径流内部特征分类预测的目的。以2013-2017年宜昌站日径流为例，采用MAPE、RMSE、TIC3个性能指标对模型进行评价。结果表明，相对于以ARMA或ANN单一模型进行预测，预测精度和稳定性明显提高。本文模型复杂度虽比单一模型要高，但日径流预测时间较长，不会因时间长度和模型复杂度而影响预测精度。另外本文主要依赖于宜昌站历史径流，由于径流受气象、地质等多方面因素影响，该方法不能完全反映径流序列未来变化趋势。下一步，将着重研究并结合流域因素对径流影响的机理，进一步提高预测精度和稳定性。

□

参考文献：

[1] Antonetti M, Scherrer S, Kienzler P M, et al. Process-based hydrological modelling: the potential of a bottom-up approach for runoff predictions in ungauged catchments [J]. Hydrological Processes, 2017,31:2 902-2 920.

[2] 孟二浩，黄生志，黄 强，等．融合大气环流异常因子的径流预报研究[J]．水力发电学报，2017，36(8)：34-42．

[3] 于瑞宏，张宇瑾，张笑欣，等．无测站流域径流预测区域化方法研究进展[J]．水利学报，2016，47(12)：1 528-1 539．

[4] 尹鑫卫，李晓玲，康燕霞，等．基于SCS-CN模型的沟垄微型集雨系统径流预测[J]．生态学杂志，2015，34(12)：3 502-3 508．

[5] 刘国东，丁 晶．BP网络用于水文预测的几个问题探讨[J]．水利学报，1999,(1)：65-70．

[6] Shoaib M, Shamseldin A Y, Melville B W, et al. A comparison between wavelet based static and dynamic neural network approaches for runoff prediction[J]. Journal of Hydrology, 2016,535:211-225.

[7] 周 娅，郭 萍，古今今．基于BP神经网络的概率径流预测模型[J]．水力发电学报，2014，33(2)：45-50．

[8] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer, 2000.

[9] 叶碎高，彭 勇，周惠成．基于PSO参数辨识SVM的中长期径流预测研究[J]．大连理工大学学报，2011，51(1)：115-120．

[10] Meng X, Yin M, Ning L, et al. A threshold artificial neural network model for improving runoff prediction in a karst watershed[J]. Environmental Earth Sciences, 2015,74(6):1-10.

[11] 卫太祥，马光文，黄炜斌．基于惩罚加权支持向量机回归的径流预测模型[J]．水力发电学报，2012，31(6)：35-38．

[12] 聂 敏，刘志辉，刘 洋，等．基于PCA和BP神经网络的径流预测[J]．中国沙漠，2016，36(4)：1 144-1 152．

[13] 李 娇，姜明媛，孙文超，等．基于BP神经网络的泉州市山美水库降雨径流模拟研究[J]．北京师范大学学报(自然科学版)，2013，49(2)：170-174．

[14] 黄巧玲，粟晓玲，杨家田．基于小波分解的日径流支持向量机回归预测模型[J]．西北农林科技大学学报(自然科学版)，2016，44(4)：211-217．

[15] Patil S K, Valunjkar S S. Utility of coactive neuro-fuzzy inference system for runoff prediction in comparison with multilayer perception[J]. International Journal of Engineering Research, 2016,5(1):156-160.

[16] 纪昌明，李荣波，张验科．等．基于小波分解的投影寻踪自回归组合模型及其在年径流预测中的应用[J]. 水力发电学报，2015，34(7)：27-35．

[17] 王秀杰，封桂敏，耿庆柱．小波分析组合模型在日径流预测中的应用研究[J]．自然资源学报，2014,(5)：885-893．

[18] Shi J, Liu Y, Yang Y, et al. Short-term wind power prediction based on wavelet transform-support vector machine and statistic characteristics analysis[C]∥ Industrial and Commercial Power Systems Technical Conference, IEEE, 2011:1 136-1 141.

[19] 高 阳，张碧玲，毛京丽，等．基于机器学习的自适应光伏超短期出力预测模型[J]．电网技术，2015，39(2)：307-311．

[20] Hartman E, Keeler J D, Kowalski J M. Layered neural networks with gaussian hidden units as universal approximations [J]. Neural Computation, 1990, 2(2):210-215.

[21] 王秀杰，练继建，费守明．基于小波消噪的混沌神经网络径流预报模型[J]．水力发电学报，2008，27(5)：37-40．

[22] 易丹辉．数据分析与EViews应用[M]．2版．北京：中国人民大学出版社，2014．

[23] 谢中华．MATLAB统计分析与应用[M]．北京：北京航空航天大学出版社，2010．