基于改进TOPSIS法的船舶通航环境风险评价模型

马全党， 江福才， 王群朋， 王 晨

(武汉理工大学 a. 航运学院; b. 内河航运技术湖北省重点实验室; c. 交通学院, 武汉 430063)

近年来，随着经济的不断发展，我国港口的吞吐量迅速增长，船舶航行安全问题愈发受到重视。船舶航行安全受到许多因素的影响，目前在船舶通航风险评价方面呈现出2种趋势：

1) 基于不确定性数学方法建立的模型，从船员、船舶、环境和管理等要素出发，对船舶通航安全进行模糊评价。[1-3]

2) 基于量化指标思想，将受主观影响大、难以通过客观量化值表示的船舶通航风险因素从指标体系中去除或用其他指标替代，基于可量化的因素，对船舶通航环境进行定量评价。[4-6]

船舶通航环境风险评价研究大多针对多个对象进行定量评价，对单个对象的风险评价以模糊评价方法为主。模糊评价方法多通过专家问卷确定指标值，评价结果的准确性易受主观因素的影响。定量评价选取可量化的指标建立指标体系，指标值为客观量化值，通过对其进行无量纲化和归一化处理，获得指标对所评价风险状况的贡献，在评价过程中消除主观因素的影响，得到更准确的结果。

逼近理想解排序法(Technique for Order Preference by Similarity to Ideal Solution，TOPSIS)是一种通过计算有限个对象与理想化目标的接近程度并排序，在现有对象中进行相对优劣评价的方法。TOPSIS的理论原理简单、计算简便、适应性和可移植性较强，广泛应用于方案决策[7-8]和风险评价[9-12]研究中；在风险评价应用中，其缺点是仅能对多个对象进行相对风险评价，无法对单个对象进行评价并得到风险等级。

在船舶通航环境风险评价研究中，为有效地对单个对象进行定量评价，并简化评价模型和计算过程，拟基于TOPSIS理论，确定多个虚拟评价对象作为不同通航风险等级的代表，称之为标准评价对象；采用熵权法确定指标权重[13-15]，建立熵权TOPSIS模型，同时对标准对象和实际对象进行评价，得到单个对象风险等级量化值。以某航道为评价实例，对航道通航环境风险进行定量评价，并与熵权物元模型评价结果相对比，验证模型的有效性和实用性，为船舶通航和管理等后续研究提供参考。

1 数学模型

1.1 建立风险判断矩阵

设有m个待评价对象，n个评价指标，xij为第i个待评价对象的第j个评价指标的取值，可得风险判断矩阵A为

A=(xij)m×n,i=1,2,…，m;j=1,2,…，n

(1)

评价指标一般具有不同的量纲和量纲单位，因此需对评价指标进行无量纲化处理，计算式为

(2)

但是，在评价指标体系中：有的指标值越大风险越大，被称为同向风险指标；有的指标值越小风险越大，被称为反向风险指标。因此，在对指标进行无量纲化之前，需对其进行同趋势化处理，即将反向指标值按相反数代入到公式中进行计算。

通过上述方法，可得到标准风险判断矩阵B为

B=(bij)m×n,i=1,2,…,m;j=1,2,…,n

(3)

1.2 确定指标权重

首先，定义各评价指标的熵，设

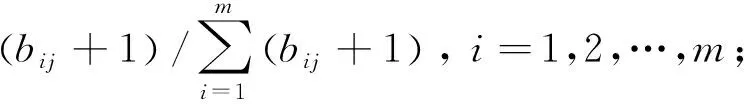
j=1,2,…,n

(4)

可得各评价指标的熵为

(5)

其次，计算各评价指标的熵权为

(6)

由此得到权重向量W为

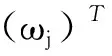
(7)

将标准风险判断矩阵与权重向量相乘可得到加权标准风险判断矩阵R为

R=(ωj·bij)m×n,i=1,2,…，m;j=1,2,…，n

(8)

令rij=ωj·bij，则R可表示为

R=(rij)m×n,i=1,2,…,m;j=1,2,…,n

(9)

1.3 计算风险贴近度

设最大风险集为S*，最小风险集为S0，则

S*=(r*j|j=1,2,…,n)=

(10)

S0=(r0j|j=1,2,…,n)=

(11)

评价对象指标值向量到最大风险集的距离D*i和最小风险集的距离D0i可表示为

(12)

(13)

式(12)和式(13)中：i=1,2,…,m；j=1,2,…,n；q的取值可根据实际问题确定，一般选择q=1(海明距离)或q=2(欧氏距离)。

计算各待评价对象的指标评价值向量与最大风险集的贴近度Fi，并通过对Fi进行排序来确定各评价对象的风险大小。

Fi=D0i/(D*i+D0i),i=1,2,…，m

(14)

2 实例应用

为确定熵权TOPSIS模型在船舶通航环境评价中定量评价单个对象风险等级的有效性，拟以某航道为研究实例，对其通航环境风险等级进行计算。

2.1 建立评价对象风险判断矩阵

通过咨询专家和查阅相关文献[6]，得到航道通航环境风险评价指标体系见表1，待评价航道和标准评价对象指标值见表2，其中：M1、M2、M3、M4和M5分别为代表“低风险”“较低风险”“一般风险”“较高风险”“高风险”的标准评价对象；M为待评价航道。

由式(1)～式(3)对指标值进行归一化和无量纲化处理之后，求得标准风险判断矩阵B。

2.2 确定评价对象指标权重

根据式(4)～式(7)求得各评价指标的权重。ω1=0.084 3,ω2=0.081 9,ω3=0.068 2,ω4=0.079 8,ω5=0.086 3,ω6=0.071 7,ω7=0.085 9,ω8=0.086 3,ω9=0.086 3,ω10=0.093 2,ω11=

表1 风险评价指标体系

0.093 2,ω12=0.084 1。

根据式(8)和式(9)求得加权标准风险判断矩阵R。

主观症状评价结果见表1。可见治疗后VAS评分较术前显著降低，差异有统计学意义 （P＜0.05）;治疗后RMDQ评分较术前显著降低，差异有统计学意义（P＜0.05）。

2.3 计算评价对象风险贴近度

根据式(10)～式(14)，求得标准评价对象和待评价对象风险贴近度见表3。由计算结果可知，各标准评价对象风险贴近度F1、F2、F3、F4和F5按等级依次增大，而待评价航道M的风险贴近度F=0.093 243，位于F1与F2之间，且更靠近F1，故待评价航道通航环境风险状况为“较低风险”，且靠近“低风险”等级。

表2 评价对象指标值

表3 待评价对象风险贴近度

3 模型验证

利用熵权物元模型[5]对评价结果的可靠性进行验证。评价对象Yi的物元为R=(Yi,Cij,vij)，i=1,2,…,m;j=1,2,…,n。

首先，计算评价对象单指标关联度，即评价对象某项指标关于某风险等级的关联程度，有

Kijp(Yi)=

(15)

|Vjp|=|bjp-ajp|

(16)

ρ(vij,Vjp)=|vij-1/2(ajp+bjp)|-1/2(bjp-ajp)

(17)

ρ(vij,Vj)=|vij-1/2(aj+bj)|-1/2(bj-aj)

(18)

其次，采用熵权法计算各项指标的权重大小，计算式如式(4)～式(7)所示。

最后，计算待评价对象Yi关于等级p的综合关联度Kip(Yi)，计算式为

(19)

文献[6]利用熵权物元模型对某5段航道通航环境风险进行评价，得到可靠的结果。利用熵权物元模型评价验证的航道通航环境风险状况见表4。

表4中：R1、R2、R3、R4和R5分别表示“低风险”“较低风险”“一般风险”“较高风险”“高风险”等级；M为评价对象；Kjp(M)为评价对象单指标等级关联度；Kp(M)为评价对象综合等级关联度。由计算结果可知，max[Kp(M)]=K2(M)=0.004 524，表示待评价M航道引航环境风险状况为“较低风险”等级；K1(M)=-0.110 94，K3(M)=-0.404 14，K4(M)=-0.321 27，K5(M)=-0.640 87，均处于(-1,0)区间内，具有转化为“低风险”“一般风险”“较高风险”“高风险”的可能性，其中K1(M)在这4个综合等级关联度中最大，表明待评价航道最易转化为“低风险”等级，与熵权TOPSIS模型评价结果一致。

表4 熵权物元模型验证结果

4 结果分析

4.1 单对象风险评价

根据熵权理论和TOPSIS模型的计算原理，单个对象既不能用熵权确定权重，也无法通过TOPSIS模型进行评价。为解决该问题，受TOPSIS模型中最大风险集和最小风险集的启发，在航道通航环境风险评价中将风险状况分为 “低风险”、“较低风险”、“一般风险”、“较高风险”和“高风险”等5个等级，并提出虚拟的标准评价对象的概念，作为各风险等级的代表，解决熵权TOPSIS模型无法对单个对象进行评价及无法确定风险等级的问题，保留风险定量评价的优势，同时使评价过程更为简单。

B=

R=

4.2 评价结果分析

一般而言，影响风险评价结果的因素包括指标权重和指标值。本文的指标权重由熵权法确定，熵权法根据信息熵理论，认为：数值间差异越大的指标包含的信息越多，对其赋予较大的权重；数值间差异越小的指标包含的信息越少，对其赋予较小的权重。

本文的评价结果由TOPSIS模型计算得出。TOPSIS模型根据评价对象与最大风险集中某项指标值之间的距离决定该对象、该指标值对最后评价结果的贡献。指标值之间距离越近，其风险贡献度越大；指标值之间距离越远，其风险贡献度越小。在该研究中，由于标准评价对象为各风险等级的代表，因此若被评价对象与代表某等级标准评价对象的某项指标值最为接近，则可认为该项指标值对整体风险的贡献最多到该等级，并以该等级的风险程度来影响最终的评价结果。

分析各评价指标的权重，发现指标C10和C11的权重最大(分别为0.092 211和0.093 191)，相应地，对应各评价对象指标值之间的差异非常大，而待评价航道这2项指标均为低风险等级；指标C3的权重最小(为0.068 150 7)，对应各评价对象指标值之间的差异较小，因此所赋权重较小；其他指标权重之间的差别较小，此处不再赘述。

分析被评价航道各项指标值，发现所有指标均距离“高风险”等级的虚拟评价对象指标值较远，除C3、C4、C5和C10之外，其余指标均位于“低风险”与“较低风险”虚拟评价对象指标值之间，表明其对最终航道通航风险的贡献介于“低风险”与“较低风险”之间。最终的评价结果亦表明，待评价航道通航环境状况为“较低风险”，接近“低风险”等级。

5 结束语

本文通过引入标准评价对象，改进熵权TOPSIS模型，解决单个对象的风险等级无法定量评价的问题。以某段航道作为研究对象，采用熵权TOPSIS模型对其通航环境风险状况进行评价，并对比熵权物元模型的评价结果，验证熵权TOPSIS模型的准确性、实用性和可靠性，丰富船舶通航环境风险定量评价相关研究成果，为船舶通航及管理等后续研究提供一定的参考。经分析，得出以下结论：

1) 熵权TOPSIS模型可分为基于待评价对象的指标体系和基于数学模型的计算方法2部分。利用熵权TOPSIS模型所得风险评价结果是否准确，在很大程度上依赖于评价对象指标体系的建立，合理选取可用客观量化值表示并能切实反映评价对象风险特征的指标是利用模型进行评价的前提。这使得熵权TOPSIS模型具有较强的适应性和可移植性，可广泛应用于其他类型单个对象的风险评价中。

2) 本文采用风险评价领域较为常用、基于信息熵理论的熵权法对指标权重进行计算，熵权法根据同类指标值之间差异大小确定权重，指标值差异越大，权重越大。但是，数值差异最大的指标并不一定是风险影响程度最大的指标。因此，如何对熵权法进行改进，使数值差异大的指标与风险影响程度最大的指标在确定权重过程中得到统一，是后续研究的重要工作。

[1] 贾明明, 熊锡龙, 黄立文, 等. 基于集值统计-灰色模糊的航道通航环境安全评价[J]. 安全与环境学报,2017,17(1): 41-45.

[2] ZHANG D, YAN X P, YANG Z L, et al. Incorporation of Formal Safety Assessment and Bayesian Network in Navigational Risk Estimation of the Yangtze River[J]. Reliability Engineering & System Safety, 2013, 118(10): 93-105.

[3] HU Shenping, ZHANG Jinpeng. Risk Assessment of Marine Traffic Safety at Coastal Water Area[J]. Navigation of China, 2012, 45(2): 31-37.

[4] CHEN Jihong, ZHANG Fangwei, YANG Chen, et al. Factor and Trend Analysis of Total-Loss Marine Casualty Using a Fuzzy Matter Element Method[J]. International

Journal of Disaster Risk Reduction, 2017,24(3):383-390.

[5] 王晨, 江福才, 马全党, 等. 基于熵权物元模型的航道引航环境风险评价[J]. 中国航海, 2017,40 (2):44-49.

[6] 吴定勇, 文元桥. 航道通航风险评价的熵权物元模型[J].武汉理工大学学报(交通科学与工程版),2014,38(5): 1158-1162.

[7] WALCZAK D, RUTKOWAKA A. Project Rankings for Participatory Budget Based on the Fuzzy TOPSIS Method [J]. European Journal of Operational Research, 2017, 260(2): 706-714.

[8] SAYAREH J, ALIZMINI H R. A Hybrid Decision-Making Model for Selecting Container Seaport in the Persian Gulf[J]. Asian Journal of Shipping and Logistics, 2014, 30(1): 75-95.

[9] KARAJALIOS H. The Application of the AHP-TOPSIS for Evaluating Ballast Water Treatment Systems by Ship Operators [J]. Transportation Research Part D: Transport and Environment, 2017, 52: 172-184.

[10] YAN X P, WAN C P, ZHANG D, et al. Safety Management of Waterway Congestions Under Dynamic Risk Conditions-A Case Study of the Yangtze River[J]. Applied Soft Computing, 2017,4(1):7-11.

[11] 王晨 ,江福才, 马全党. 基于熵权TOPSIS模型的航道引航环境风险评价[J]. 安全与环境学报, 2016, 16(3):33-37.

[12] OTHMAN M K, FADZIL M N, RAHMAN N S F A. The Malaysian Seafarers Psychological Distraction Assessment Using a TOPSIS Method[J]. International Journal of E-Navigation and Maritime Economy, 2015, 3: 40-50.

[13] BERUVIDES G, QUIZA R, HABER R E. Multi-Objective Optimization Based on an Improved Cross-Entropy Method: A Case Study of a Micro-Scale Manufacturing Process[J]. Information Sciences, 2016, 334: 161-173.

[14] LIN Rongtai, TAN Jian. Evaluation of Port Development Based on the Theory of the Driving Force and the Law of Entropy Weight[J]. Procedia-Social and Behavioral Sciences, 2013, 96: 1774-1783.

[15] DENG Xiaojun, XU Youpeng, HAN Longfei, et al. Assessment of River Health Based on an Improved Entropy-Based Fuzzy Matter-Element Model in the Taihu Plain, China[J]. Ecological Indicators, 2015, 57: 85-95.