弹箭磁屏蔽效能仿真及分析

韩 宇,李东阳,邱海迪

(1. 海军驻沈阳弹药专业军事代表室,辽宁 沈阳 110045;2. 南京理工大学 能源与动力工程学院,江苏 南京 210094)

近年来,精确制导武器的研制和常规武器制导化的研究逐渐成为热点,为提高武器的效费比,需要在提高武器打击精度的同时降低制导控制等各环节的成本[1]。地磁导航以其低成本、安装操作简便等优点被广泛应用,地磁传感器成为姿态测量技术的热点之一。因为磁传感器自身和工作环境等多种因素,磁场测量值和真实磁场之间存在误差[2]。对于磁传感器的测量误差的研究,前人也已经做出了许多创造性的工作[3-6]。现有的利用磁传感器求解姿态矩阵的方法需要求解3个姿态角,方程非线性强且不利于分析解的存在性[7]。

本文主要研究弹体材料的磁屏蔽效应对地磁测量误差的影响,利用ANSYS对弹体的磁屏蔽特性进行仿真分析,研究弹体材料、厚度、姿态角等因素对弹体磁屏蔽效应的影响规律;推导了姿态角和磁屏蔽系数之间的关系,提出了利用磁屏蔽椭球模型直接得到误差矩阵后进行磁测误差校正的方法,减少了拟合数据反解误差矩阵的计算量。提出利用磁屏蔽椭球模型直接解算弹体相对于地磁矢量的2个姿态角的方法,直接得到了弹体和地磁矢量之间的空间关系,为磁传感器在弹上的应用提供理论基础。

1 弹体磁屏蔽系数模型

由于弹体材料的磁阻远低于大气环境的磁阻,弹体会对地磁造成屏蔽作用。弹体的磁屏蔽效应将造成位于弹体内部的磁传感器的测量误差。

磁屏蔽系数可以量度铁磁材料的磁屏蔽效果。假设不存在弹体时某处的磁场强度为H0,磁感应强度为B0;存在弹体时的磁场强度为Hs,磁感应强度为Bs。则磁介质对外加磁场的屏蔽系数S一般可以表示为[8]

(1)

本文即采用磁屏蔽系数S来评估弹体的磁屏蔽效果,S越大则磁屏蔽效果越强。对于长径比较大的弹体,当磁场方向垂直于弹体纵轴时,可以简化为研究无限长圆柱腔的磁屏蔽效能,如图1所示,其磁屏蔽系数为[8]

(2)

式中:r1和r2分别为弹体的内、外半径;μr为弹体相对磁导率。

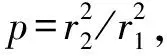
(3)

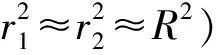
(4)

式中:弹体壁厚δ=r2-r1,弹体平均半径R=(r1+r2)/2。该式表明在满足约束条件的情况下,弹体的静磁屏蔽系数与相对磁导率、弹体壁厚成正相关,与弹体平均半径成负相关,与外加磁场大小无关。下面利用表1给出的弹体参数计算磁屏蔽系数S=2.92。表中,L为弹长。

表1 弹体参数

2 弹体磁屏蔽仿真

2.1 弹体二维磁屏蔽仿真

磁屏蔽系数解析表达式因其假设而存在一定的局限性,随着计算能力的提高,计算机仿真结果有时更加接近实际情况,可以在一定程度上为工程和研究提供更加准确的参考依据。由于本文主要研究弹体对地磁场的磁屏蔽效应,对弹体进行二维磁屏蔽进行仿真时,利用ANSYS中的Electromagnetic模块,选用PLANE53单元建模,在分析中用设置自由度磁矢量(AZ)的值得到恒定磁场来模拟地磁场。空气区域尺寸是长为2 m且宽为1 m的矩形区域,相对磁导率设为1,弹体尺寸参见表1,相对磁导率μr=50。由于弹体磁屏蔽效应与外加磁场大小无关,所以仿真中施加B0=10 T的均匀平行磁场模拟地磁场(约为5.4×10-5T),图2为求解得到磁力线分布图。

利用路径分析法获取弹体内部空间的磁感应强度Bs,选取沿x轴方向的路径lx和沿y轴方向的路径ly,磁感应强度分布曲线如图3所示。

由图3可知,经过弹体后磁感应强度迅速减小,并在弹体空腔内处于一个稳定值,但是在靠近弹体附近沿lx和ly路径的磁感应强度变化有所不同。从弹体外部沿lx路径靠近弹体时,磁感应强度逐渐增大;而沿ly路径靠近弹体时,磁感应强度先有小幅度减小后又迅速增大到更大值,峰值几乎是前者的4倍,这是因为弹体的相对磁导率较大造成对磁感线的吸引。此时,弹体内部磁感应强度Bs=3.32 T,则当磁场垂直弹体纵轴时,弹体的磁屏蔽系数为

(5)

与式(2)计算得到的理论值2.92的相对误差为[(3.01-2.92)/3.01]×100%≈2.99%,相差较小,说明仿真结果具有较高可信度。

由于理论计算模型是无限长圆柱腔体,是三维模型,而后文进行三维磁场仿真得到该情况下弹体磁屏蔽系数为2.80,可见当磁场垂直于弹体纵轴时,可用弹体圆柱截面的二维仿真来代替三维仿真,这对研究弹体磁屏蔽系数带来极大的方便,但进一步仿真发现,弹体纵截面的二维仿真不能代替弹体的三维仿真。

仅改变弹体材料的相对磁导率μr,分析弹体对磁场分布的影响;仅改变弹体内半径以分析弹体壁厚δ对磁场分布的影响。计算结果如图4和图5所示。

从图4和图5可知,磁屏蔽系数随弹体相对磁导率的增大而增大,随弹体壁厚的增大而增大,与理论公式分析结果一致,进一步验证了理论公式和仿真结果的可信度。

2.2 弹体三维磁场仿真

弹体磁屏蔽系数不仅与弹体的材料和结构特性有关,还与弹体相对于空间磁场的姿态有关。由于弹体是轴对称体,所以只需研究磁屏蔽系数随弹体纵轴与磁场方向的夹角变化规律即可得到弹体磁屏蔽系数随弹体姿态的关系。由于磁场方向不再垂直于弹体纵轴,前述的理论模型(式(2))不再成立,因此需要进行三维磁场仿真。

采用SOILD96单元和RSP求解方法,有限元仿真的主要步骤和二维分析基本一致。建立边长为4 m的正方体区域(如图6所示),弹体纵轴沿x轴,沿x轴正方向施加B0=10 T的均匀平行磁场。

其他参数不变,仿真得到的弹体磁感应强度矢量分布图和纵向截面的磁感应强度矢量分布图如图7和图8所示。同样选择沿弹轴的路径l得到磁感应强度变化如图9所示。

图9中,弹体位置在-0.5～0.5 m处,从曲线能够看出,远离弹体区域磁感应强度为10 T,与仿真地磁场的大小基本相同;靠近弹体尾部(x=-0.5 m)时,磁感应强度增大至13.56 T;进入弹体内部,磁感应强度快速减小后又缓慢增大然后稳定在6.90 T;接近弹头顶端(x>0.30 m)时,磁感应强度迅速升高,在x=0.49 m时达到极大值795.06 T,这是由于弹体中圆锥形头部对磁感应线的吸引作用造成的;远离弹体(x>0.50 m)后磁感应强度又快速降低到和外加磁场大小相同。圆锥形头部磁感应强度的急剧变化也说明了弹体形状会影响弹体的磁屏蔽效果,因此磁传感器应该安装在弹体圆柱段中心部位,且周围的构造尽量简单,没有其他复杂铁磁性材料结构的干扰。由此可以计算,在磁感应强度稳定的弹体中心磁屏蔽系数为

2.3 弹体姿态对磁屏蔽效应的影响

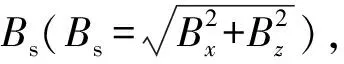
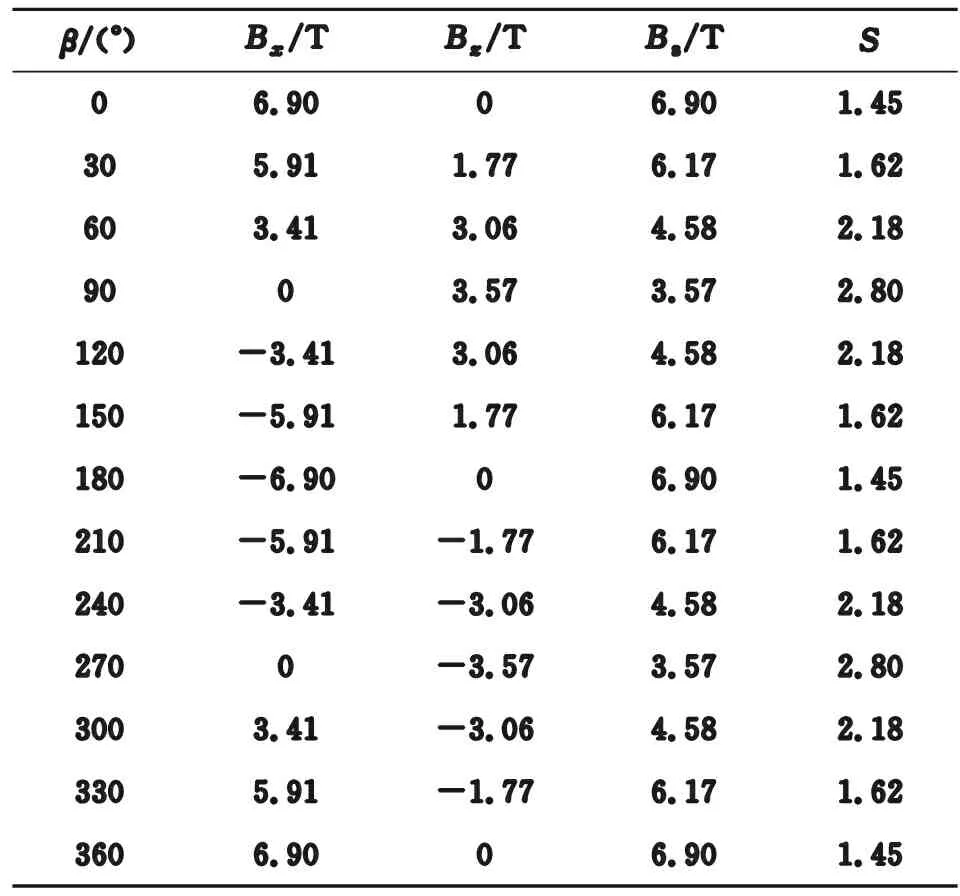
表2 弹体不同姿态角三维磁屏蔽仿真结果

由表2可以看出,弹体中心点的磁感应强度随弹体姿态变化而变化:当β=0或180°时,即弹丸纵轴与磁场方向平行时,磁感应强度最大,弹体磁屏蔽系数最小;当β=90°或270°时,即弹丸纵轴与磁场方向垂直时,磁感应强度最小,弹体磁屏蔽系数最大,S=2.80,大小与二维仿真结果(5)基本一致,且均和“无限长圆柱腔的理论模型(式(4))”的计算结果S=2.92吻合,这也验证了无限长圆柱腔的理论模型和ANSYS仿真结果的可信性。

同时进行了弹体纵截面的二维磁屏蔽仿真,结果如表3所示。

表3 弹体磁屏蔽系数三维仿真和二维纵截面仿真的结果对比

从表3可知,弹体的二维纵截面磁屏蔽效果仿真结果不仅在数值上和三维仿真结果差别较大,而且随弹体姿态角的变化趋势也相反,对比结果说明弹体的三维磁场仿真不能简化为二维纵截面磁屏蔽仿真。因此,文献[6]中利用二维纵截面的仿真结果来代替三维仿真结果是不严谨的。此外,文献[6,9]中所用到的“矩形截面屏蔽盒低频磁屏蔽效能近似计算公式”计算结果和弹体的三维磁场仿真结果相差甚远,认为对弹体磁屏蔽效应的研究不具有指导意义。

将表2中测试点磁感应强度数据显示在Bx-Bz平面上,得到曲线如图10所示,拟合图10中仿真结果曲线得到椭圆方程:

式中:a′=6.90 T,b′=3.57 T,仿真和理论分析发现,a′和b′分别为弹体纵轴平行、垂直地磁场方向时弹体中小点的磁感应强度。

理论上不存在弹体铁磁干扰时,测试点磁感应强度应不变,仍为地磁场强度B0,Bx-Bz平面上曲线应为以原点为中心的圆:

式中:a1=b1=B0=10 T。

根据拟合方程可将不存在弹体干扰时的磁场矢量B和存在弹体干扰时的磁场矢量B′写成极坐标形式:

则

地磁场强度大小为B0,则:

磁屏蔽系数可以表示为

(6)

3 弹体磁屏蔽椭球模型及应用

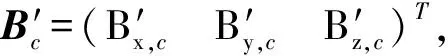
代入拟合椭圆方程得:

上式写成极坐标形式:

(7)

式中:β为弹轴正向与地磁矢量的夹角,φ为弹轴和地磁矢量所在平面与弹体纵向平面的夹角。

同理,可得:

(8)

软磁误差矩阵为

综上可知,存在弹体铁磁屏蔽时,三轴磁感应强度测量值分布为椭球型;而不存在弹体铁磁屏蔽时,分布为球形。在弹体磁屏蔽的椭球模型上,弹体不同姿态下磁传感器三轴的磁感应强度的测量值与弹体铁磁屏蔽椭球上的点一一对应,也即对应弹丸相对于地磁矢量的一种空间姿态。a′和b′可由试验测量得到,进而计算得到软磁误差矩阵Svet3,由式(8)即可进行磁测数据的校正,得到不存在弹体干扰时弹体三轴上的磁测数据,与传统的通过数据拟合反解软磁误差矩阵相比[6],该方法充分利用了磁屏蔽椭球模型的理论成果,减少了计算量以及计算可能引入的误差,为磁测数据校正问题的研究提供了一定的帮助。利用校正后的磁测数据可以进行弹体姿态角的解算[6]。同时利用式(7)可以直接解算出地磁矢量相对于弹体的2个姿态角β和φ,也即弹体相对于地磁矢量的姿态角,进而结合已知的地磁场信息,可以解算所需的弹体姿态角。

4 结论

本文建立了弹体磁屏蔽理论模型,并进行了ANSYS仿真分析。

①验证了理论和仿真结果均有较高可信度;分析磁屏蔽二维仿真和三维仿真之间的关系,得到弹体纵截面的磁屏蔽仿真不能代替弹体三维磁屏蔽仿真的结论;

②结合弹体三维磁场仿真,研究了弹体姿态角对弹体磁屏蔽系数的影响,当弹轴与磁场方向平行时磁屏蔽系数最小,随着夹角的增大,磁屏蔽系数增大,当弹轴与磁场方向垂直时,磁屏蔽系数最大;

③通过椭圆拟合得出了弹体磁屏蔽系数随弹体姿态角的变化关系,建立了弹体磁屏蔽椭球模型,提出了直接获取磁测修正矩阵即软磁误差矩阵的方法;提出利用磁测数据直接解算弹体相对于地磁场的姿态角的思路,为进一步获取需要的弹体姿态角提供了帮助。

[1] 刘勇,沈毅,胡恒章,等. 精确制导武器及其支持系统中的信息融合技术[J]. 系统工程与电子技术,1999,21(4):1-5.

LIU Yong,SHEN Yi,HU Hengzhang,et al. Technique on information fusion for accurate guidance weapon and its supporting systems[J]. Journal of Detection and Control,1999,21(4):1-5. (in Chinese)

[2] 王宇,张晓明,白渚铨,等. 基于有限元的弹体磁屏蔽效能分析[J]. 弹箭与制导学报,2013,33(4):12-14.

WANG Yu,ZHANG Xiaoming,BAI Zhuquan,et al. The analysis of geomagnetic field shielding coefficient of projectile body based on finite element[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(4):12-14. (in Chinese)

[3] 龙礼,张合,刘建敬. 姿态检测地磁传感器误差分析与补偿方法[J]. 中国惯性技术学报,2013,21(1):80-83.

LONG Li,ZHANG He,LIU Jianjing. Error analysis and compensation methods of magnetometer for attitude measurement[J]. Journal of Chinese Inertial Technology,2013,21(1):80-83. (in Chinese)

[4] 黄学功,王炅. 地磁信号检测系统误差分析与补偿方法研究[J]. 兵工学报,2011,32(1):33-36.

HUANG Xuegong,WANG Jiong. Error analysis and compensation methods for geomagnetic signal detection system[J]. Acta Armamentarii,2011,32(1):33-36. (in Chinese)

[5] 李勇,刘文怡,李杰,等. 基于椭球拟合的三轴磁传感器误差补偿方法[J]. 传感技术学报,2012,25(7):917-920.

LI Yong,LIU Wenyi,LI Jie,et al. Error compensation method for three-axis magnetic sensor based on ellipsoid fitting[J]. Chinese Journal of Sensors and Actuators,2012,25(7):917-920. (in Chinese)

[6] 邱海迪. 基于磁传感器弹箭姿态解算影响因素研究[D]. 南京:南京理工大学,2017.

QIU Haidi. Research of influential factors of attitude algorithm based on magnetic sensor for projectile[D]. Nanjing:Nanjing University of Science & Technology,2017. (in Chinese)

[7] 陈春行,林春生,贾文抖,等. 基于地磁传感器的弹体姿态测量方法[J]. 探测与控制学报,2018(1):33-35,39.

CHEN Chunxing,LIN Chunsheng,JIA Wendou. The projectile attitude measuring method based on geomagnetic sensor[J]. Journal of Detection & Control,2018(1):33-35,39. (in Chinese)

[8] 路宏敏,余志勇,李万玉. 工程电磁兼容[M]. 西安:西安电子科技大学出版社,2010.

LU Hongmin,YU Zhiyong,LI Wanyu. Engineering electromagnetic compatibility[M]. Xi’an:Xi’an Electronic Science and Technology University Press,2010. (in Chinese)

[9] 高峰,张合. 弹体磁屏蔽效能的计算与仿真[J]. 计量学报,2010,31(2):141-144.

GAO Feng,ZHANG He. Calculation and simulation of geomagnetic field shielding effectiveness of projectile body[J]. Acta Metrologica Sinica,2010,31(2):141-144. (in Chinese)