一种求解平面热传导反问题的新型无网格方法

王婷婷，王发杰，张耀明

(山东理工大学 数学与统计学院， 山东 淄博 255049)

数学物理反问题源于物理、生物、医学、地质等众多科学领域中的实际问题。反问题是相对于正问题而言，主要包括Chauchy问题、源项识别问题、参数识别问题、初值反问题、几何形状反问题和自由边界反问题等。在实际工程应用中，由于受到工况条件或设备条件的限制，仅能测量部分结构的边界温度和热流，其余边界上的边界条件无法获取，这类反问题就是所谓的Chauchy热传导反问题[1]。Chauchy热传导反问题由于可利用边界信息较少，传统数值方法大多对测量边界误差非常敏感，通常会产生不适定问题，从而难以得到可接受的数值解。近年来，诸多研究者开始关注和探究这类反问题的数值方法。

有限元法(FEM)和有限差分法(FDM)长久以来是实际工程应用中的主流数值计算方法，已被广泛应用于反问题的研究中。但是，这些基于网格类的方法需要对整个计算区域进行离散，过程繁琐且耗时，特别是对于无限域问题和高维的不规则几何形状问题。此外，反问题已知部分边界条件时，有限元模拟相当困难且计算精度不高。边界元法(BEM)将问题维数降低一维，并具有边界离散和半解析性质，是目前较有潜质的一种数值算法[2]，在热传导反问题的求解中，比有限元法更有效、更准确。然而，边界元法不可避免地涉及奇异积分和几乎奇异积分的计算，这就为解决实际问题带来了很大困扰。针对此情况，笔者[3-4]提出了一种简单精确的无网格方法—平均源边界点法。该方法基于规则化边界积分方程[5-6]，通过加减去奇异和平均积分的思想，消除了基本解的源点奇异性，具有无网格、无积分、仅需边界离散、半解析的特性，目前已成功应用于位势问题的研究。

本文是平均源边界点法在模拟平面热传导Cauchy反问题的第一次尝试。众所周知，数值模拟方法所建立的不适定系统往往高度病态，微小的边界数据扰动可能会导致极大的计算误差。无网格法已广泛应用于Helmholtz方程问题[7]、含源项热传导方程[8]等方面。本文利用新的无网格方法—平均源边界点法求解平面二维热传导Cauchy反问题，采用截断奇异值分解(TSVD)和Tikhonov正则化技术[9-10]求解病态线性方程组，通过广义交叉校验准则(GCV)来确定正则化参数[11-12]。所提出的方法无需网格划分，避免了奇异积分计算，是一种简单精确的无网格方法。本文为平面热传导反问题的研究开辟了新的途径，拓展了平均源边界点法的应用领域。数值试验结果表明了所提方法的有效性、稳定性和精确性。

1 平面热传导反问题的平均源边界点法

1.1 控制方程

本文假定问题的区域为有界区域Ω⊂R2，其边界为Γ=∂Ω。总是假定边界由两部分组成，Γ=Γ1∪Γ2，这里Γ1,Γ2≠∅，Γ1∩Γ2=∅，函数u(x)满足Laplace控制方程：

(1)

边界条件为：

(2)

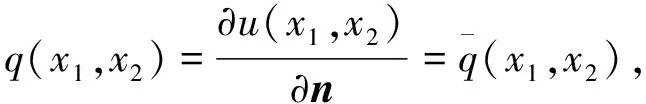
(x1,x2)∈Γ1

(3)

控制方程(1)的基本解为

(4)

其中|x-y|表示两点x和y之间的欧几里得距离。

1.2 平均源边界点法

为了避免直接计算强、弱奇异积分，本文方法基于文献[3-4]的间接平均源边界积分方程：

(5)

其中：Gij、Hij为系数矩阵；N为总的边界节点数；uj、qj是节点j处的温度和法向通量。Gij、Hij表示为：

(6)

(7)

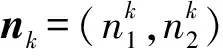
远离边界的内部点y的温度和温度梯度可表示为：

(8)

(9)

(10)

其中rk=xk-yk。

2 正则化方法

2.1 截断奇异值分解(TSVD)

考虑如下线性方程组：

Ax=b

(11)

其中：A∈Rm×n；x∈Rn；b∈Rm，且m≥n。对矩阵A进行奇异值分解，有

(12)

其中：U=(u1,…,uM)和V=(v1,…,vN)分别满足UTU=IM，VTV=IN；∑=diag(σ1,…,σN)表示非负对角矩阵。

截断奇异值分解(TSVD)是一种常用的正则化方法，其基本思想[9]是用K阶矩阵AK来逼近M×N阶矩阵A。其中，AK可以表示为

(13)

这里K为正则化参数，与之对应的截断奇异值为

(14)

2.2 Tikhonov正则化方法

Tikhonov方法是一种应用比较广泛且能有效地解决病态问题的正则化方法，其基本思想[10]如下：

把正则化泛函

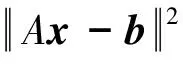
(15)

的极小元xα作为方程Ax=b的解，可表示为如下形式：

(16)

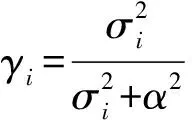
2.3 广义交叉校验准则

广义交叉校验准则(GCV)由Golub[12]提出，该方法以正则化参数K为参变量，寻求GCV函数的最小值。当求得GCV的极小值时，对应的K值为最优值。G(K)的计算公式为

(17)

其中AI满足：

可用来产生正则化参数。

3 数值算例

在实际的工程计算中，被测量的边界值会不可避免地受扰动的影响。本文的数值算例中采用以下公式[13]来增加边界数据扰动：

(18)

其中：bi是精确解；rand是一个-1～1的随机数；δ表示扰动幅度。为了评估数值解的有效性，引入下列平均相对误差[13]：

Average relative error=

(19)

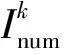
3.1 算例1：齿轮型区域

首先，考虑齿轮型区域中的稳定温度场问题。该区域由两部分组成：内部边界Γ2为半径r=0.5的圆域；外部边界Γ1的参数方程为

2(n+1)cos(nφ-nπ/2)], 0≤φ≤2π}

其中n=6。边界Γ2上的温度和通量未知，但边界Γ1上的温度和通量均可获得，问题的解析解为

u(x1,x2)=ex1cosx2

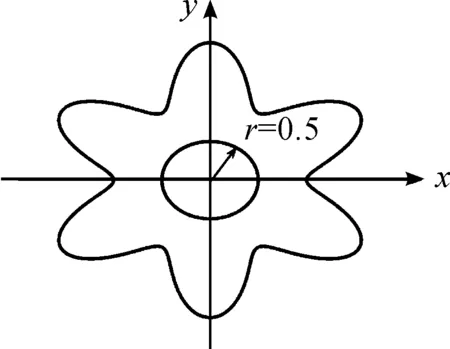
图1 齿轮型区域

计算时，内、外边界分别划分为60、120个节点。分别使用TSVD和Tikhonov正则化方法对问题进行求解，并用GCV法选取正则化参数。如图2、3所示，两种方法分别在k=126和λ=0.01处取得最优正则化参数。

图2 GCV法参数选取

图3 未知边界上数值解与解析解对比

图4描述了两种正则化方法下求得的未知边界的温度和通量的数值解与解析解的比较，从图中可以看出，所求结果与解析解十分吻合。

3.2 算例2：三圆环区域

考虑三圆环区域的稳定温度场问题，多连通区域如图4所示。内边界Γ2和Γ3的温度和通量都不可获得，但外边界Γ1的温度和通量已知且温度场的精确解为

u=r2cos(2θ)+rsinθ

图4 多连通区域(r1=2,r2=0.5,r3=0.25,a=1.0)

图5描绘了两种正则化方法的温度、通量在无扰动和3%扰动程度下的精确解与本文计算结果的比较。表1给出了不同扰动下GCV法选取的正则化参数，发现在k=130和λ=1.00×10-3处可获得最优参数。从图中可以看出，在已知条件存在随机扰动的情况下，边界温度和通量与精确解能较好地吻合，两种方法均能求得较好的结果。

图5 未知边界上温度和通量在无扰动及添加3%扰动下数值解与解析解对比

正则化方法0%1%3%5%TSVD法130130130130Tikhonov法4.040 3×10-54.040 3×10-53.418 2×10-53.418 2×10-5

3.3 算例3：四圆环区域

考虑四圆环区域上的稳态温度场问题，如图6所示。外边界Γ1的边界条件已知且温度场的精确解为

其中内边界的温度和通量未知。假设边界节点在这4部分边界上的分布为Γ1∶Γ2∶Γ3∶Γ4=7∶1∶1∶1。

图6 四圆型区域(r1=2,r2=r3=r4=0.25,a=1.0)

图7给出了未知边界温度和通量的平均相对误差曲线。分别将边界划分成100、200、300、400、500、600个节点，表2给出了不同节点数时 GCV法和TR法选择的最优正则化参数。从图7可以看出：随着单元数的增加，边界温度、通量的平均相对误差呈现明显下降的趋势，表明该方法具有较好的收敛性；仅使用100个边界节点所求得的温度及通量的相对误差在10-2～10-1，说明该方法对位势反问题可进行有效的计算求解。

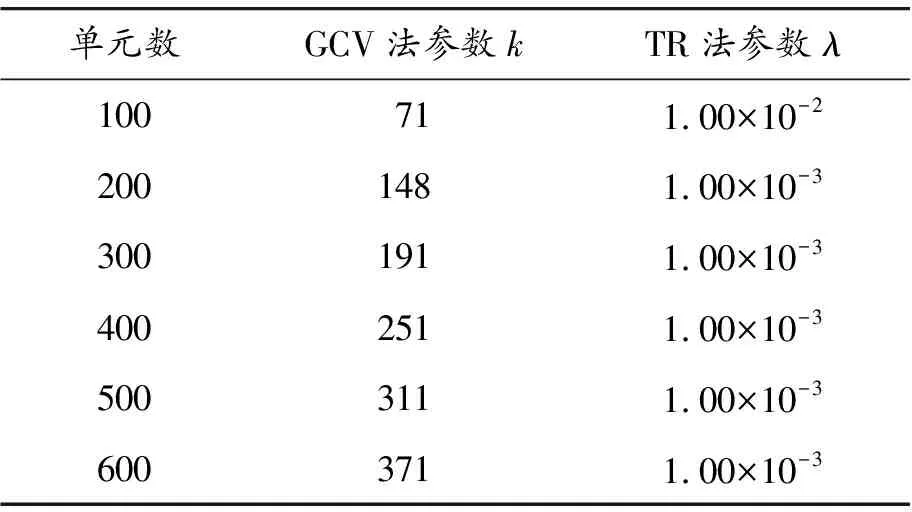
表2 不同节点数下正则化参数的选取

图7 不同节点数下未知边界温度和通量的平均相对误差

4 结束语

本文首次采用平均源边界点法(ASBNM)求解二维Cauchy热传导反问题。对求解中产生的不适定线性系统，采用TSVD和Tikhonov技术结合GCV的正则化方法来求解。与其他现有的求解病态的Cauchy热传导反问题的方法相比，该方法无积分计算、无网格，具有计算精度高、收敛速度快、程序实现简单、适合于高维问题等优点，是一种真正意义上的无网格数值方法。

通过3个经典的数值算例测试了复杂多联通区域上的热传导反问题，数值结果表明了方法的精度和有效性。本文为Cauchy热传导反问题求解提供了新的求解思路，同时拓宽了平均源边界点法的应用范围。

[1] WANG Fajie,CHEN Wen,QU Wenzhen,et al.A BEM formulation in conjunction with parametric equation approach for three-dimensional Cauchy problems of steady heat conduction [J].Engineering Analysis with Boundary Elements,2016,63(114):1-14.

[2] CHENG A H D,CHENG D T.Heritage and early history of the boundary element method [J].Engeering Analysis with Boundary Elements,2005,29(3):268-302.

[3] ZHANG Yaoming,SUN Fangling,YOUNG Derliang,et al.Average source boundary node method for potential problems [J].Engeering Analysis with Boundary Elements,2016,70:114-125.

[4] SUN Fangling,ZHANG Yaoming,YOUNG Derliang,et al.A new boundary meshfree method for potential problems [J].Advances in Engineering Software,2016,100(C):32-42.

[5] ZHANG Yaoming,SLADEK V,SLADEK J,et al.A new boundary integral equation formulation for plane orthotropic elastic media [J].Applied Mathematical Modelling,2012,36(10):4862-4875.

[6] 张耀明,屈文镇,陈正宗.三维位势问题新的规则化边界元法[J].中国科学(G辑),2013,43(3):297-308.

[7] CHEN Wen,FU Zhuojia.Boundary Particle Method for Inverse Cauchy Problems of Inhomogeneous Helmholtz Equations [J].Journal of Marine Science and Technology-Taiwan,2009,17(3):157-163.

[8] FU Zhuojia,CHEN Wen,ZHANG Chuanzeng.Boundary Particle Method for Inverse Cauchy inhomogeneous potential problems [J].Inverse Problems in Science and Engineering,2012,20(2):189-207.

[9] HANSEN P C,SEKII T,SHIBAHASHI H.The modified truncated SVD method for regularization in general form [J].Society for Industrial and Applied Mathematics,1992,13(5):1142-1150.

[10] SCHERZER O.The use of Morozov’s discrepancy principle for Tikhonov regularization for solving nonlinear ill-posed problems [J].Computing,1993,51(1):45-60.

[11] 师晋红,傅卓佳,陈文.用边界粒子法求解柯西反问题的数值计算软件包[J].计算机辅助工程,2013,22(1):64-70.

[12] GOLUB G H,HEATH M,WAHBA G.Generalized cross-validation function for ill-conditioned least squares problems [J].Technometrics,1979,21(2):215-223.

[13] GU Yan,CHEN Wen,FU Zhuojia.Singular boundary method for inverse heat conduction problems in general anisotropic media [J].Inverse Problems in Science & Engineering,2014,22(6):889-909.