以隐形圆为背景编拟问题的新视角*
●
(大厂高级中学,江苏 南京 210044)
文献[1]介绍了以阿波罗尼斯圆为背景编拟试题的新方法.在这些问题中,阿氏圆是隐形的,解题中需通过求轨迹将圆化隐为显,再研究它的几何性质.“隐形”“求轨迹”是求解的关键词,也是编拟试题的两种手段.如何将圆在题面中“隐藏”起来,除阿氏圆外,不外乎圆的轨迹定义,即平面内到定点的距离等于定长的点的轨迹是圆,编拟试题时将“定点”和“定长”用其他几何关系或数量关系来描述.这类试题题面新颖,解法基本且多样,能较好地考查学生对基本概念的理解能力,审题、转化和解决问题的能力.本文介绍这方面的新颖试题,以馈读者.
视角1化隐为显轨迹圆.
设计方法将隐形圆包装在一个数量关系等式中,通过“建(系)设(点)限(制条件)代(入)化(简)”,求出关键点的轨迹方程即圆的方程.
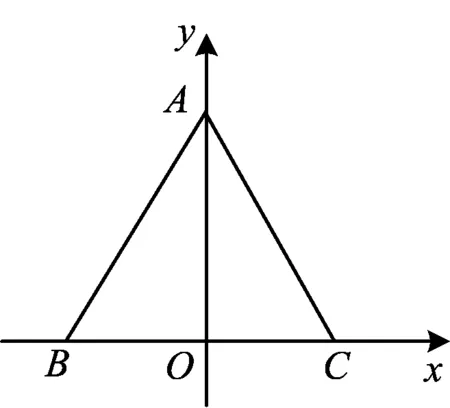
图1
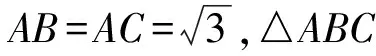

m2+h2=3.
设P(x,y),由PB2+PC2=3,得


又3PA2=3,即PA=1,点P在以点A为圆心、1为半径的圆上.因此,
设△ABC的面积为S,则


图2
例2如图2,在平面直角坐标系xOy中,已知点A(-4,0),B(0,4),从直线AB上一点P向圆x2+y2=4引两条切线PC,PD,切点分别为C,D.记线段CD的中点为M,求线段AM长的最大值.

直线AB的方程为y=x+4,点P在AB上,从而
即y-x=4λ.
(1)
由于Rt△COP∽Rt△MOC,于是
CO2=OM·OP,
即
亦即x2+y2=4λ.
(2)
由式(1)和式(2),得
x2+y2=y-x,
即


评注事实上,不难将例2一般化,只要直线AB与⊙O相离,点M的轨迹都是圆;而当直线AB与⊙O相交时,只要点P还在⊙O外,点M仍然在一段圆弧上.本题的核心是求出点M的轨迹,剩下的事就简单了.
视角2相关点求伴随圆.
设计方法点A在已知⊙C上,点B是点A的相关点,当点A变化时,点B的轨迹若是圆(记为⊙D),则称⊙D为⊙C的伴随圆.通常从点A到点B用几何变换实现,如平移、对称、伸缩等.

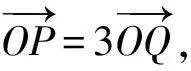
因为点Q在圆x2+(y-1)2=1上,即
所以
即
x2+(y-3)2=9,
因此点P的轨迹是以C(0,3)为圆心、半径为3的圆.

评注点Q在已知圆上运动,随之变化的点P的轨迹也是圆,用“相关点法”求点P的轨迹方程,再研究这个圆与已知直线的关系.显然,本题也可以由点P求点Q的轨迹(伴随直线),再研究该伴随直线与已知圆的关系.

分析设线段AB的中点为M,则CM⊥AB.在Rt△CAM中,
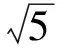
(x+4)2+(y-a)2=5.
因为M是线段AB的中点,所以
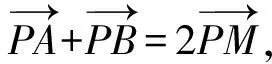
即

设M(x,y),P(x0,y0),则
从而
于是点M(x,y)在圆(x+4)2+(y-a)2=5上,因此

解得
a=2或a=-18.

视角3张角为定也是圆.
设计方法与某线段所张的角为定角的顶点轨迹是圆(弧).特别地,张角为直角时轨迹是圆,且该线段为圆的直径.某些条件隐含定角,只需根据定角,挖出圆(弧),再进一步转化位置关系.
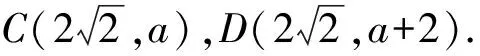
分析线段AB的中点为M,则OM⊥AB.在Rt△OAM中,
从而点M在圆心为O、半径为2的圆上,其轨迹方程为
x2+y2=4.
又以CD为直径的⊙E方程为
当点A,B在⊙O上运动时,即点M在圆x2+y2=4上运动时,始终有∠CMD为锐角,即点M始终在⊙E外,从而圆x2+y2=4与⊙E相离,即
OE>1+2=3,
亦即
解得a<-2或a>0.故实数a的取值范围是(-∞,-2)∪(0,+∞).
评注这里有两个隐形圆:一是点M的轨迹,由于⊙O及其弦长AB为确定的,从而弦中点M的轨迹是⊙O的同心圆;二是“∠CMD为锐角”的等价条件“M在以CD为直径的圆外”,将几何条件转化为两个隐形圆的位置关系.
视角4类似比值阿氏圆.
阿氏圆模型的特征是距离之比为常数,那么距离的平方之比为常数呢?显然,本质是一样的.请看下面一道改编的应用题.
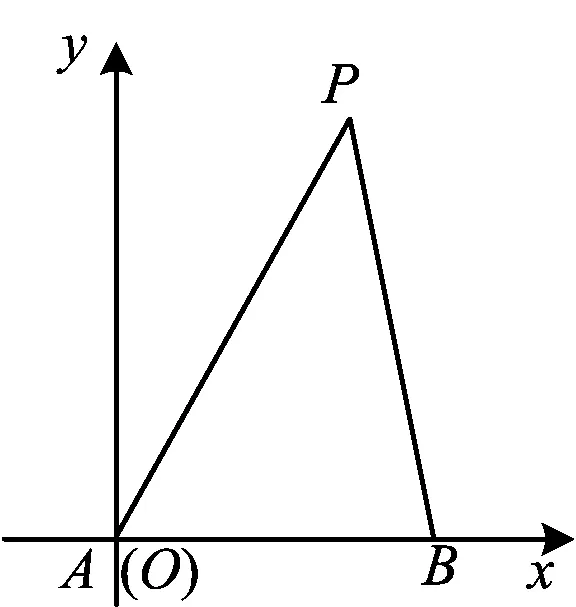
图3
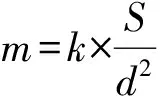

2)若要使与商场B相距2 km以内的区域(含边界)均为商场B相对于A的“更强吸引区域”,求λ的取值范围.
分析设商场A,B的面积分别为S1,S2,点P到A,B的距离分别为d1,d2,则
其中k为常数,k>0.以AB所在直线为x轴、A为原点建立如图3所示的平面直角坐标系,则A(0,0),B(10,0).设P(x,y),

即
从而
化简得
此即商场B相对于A的“更强吸引区域”.

所以点P不在商场B相对于A的“更强吸引区域”.
2)由m1 将S2=λS1代入,得 从而 (x-10)2+y2<λ(x2+y2), 化简得 (1-λ)x2+(1-λ)y2-20x+100<0. 因为0<λ<1,配方得 与商场B相距2 km以内的区域(含边界)是:圆心为B(10,0)、半径为r2=2的圆的内部及圆周. 由题设,⊙B内含于⊙C,即BC<|r1-r2|. 因为0<λ<1,所以 整理得 圆是高考的重点也是热点内容之一,反复考查,在形式上逐年推陈出新.除了熟悉的阿波罗尼斯圆外,本文介绍了在命题中常用的几种把圆隐藏在题面中的方法.像这样来源于数学史、数学定义的题型是我们取之不竭的宝库,若在平时的教学中教师能够较多地进行渗透,不断地变换视角、改编挖掘,则将更有利于提高习题的教学质量,培养学生的数学学习兴趣,促进学生创造思维的发展. 参 考 文 献 [1] 余建国.以阿氏圆为背景编拟问题的新视角[J].中学教研(数学),2015(7):16-18.

