考虑轮辐刚度和齿廓修形的渐开线直齿轮动载荷研究

李春明， 王成， 杜明刚， 赵志刚

(1.中国北方车辆研究所 车辆传动重点实验室， 北京 100072； 2.陆军装备部 项目管理办公室， 北京 100072)

0 引言

随着车辆传动系统向高速、重载的方向发展，在内、外激励共同作用下传动系统产生较强振动，降低了安全性、可靠性和工作质量，严重时甚至造成齿轮、传动轴和轴承等零件的破坏。以往针对高速重载车辆传动系统动态性能研究主要以线性扭转振动为主[1-2]，实际上传动系统的振动形式包括扭转振动、弯曲振动等，并且这些振动大多是以相互耦合的形式存在的[3-4]。间隙、时变刚度和加工误差等成为齿轮传动系统动力学研究中重要的非线性因素[5]。

修形是降低齿轮传动系统振动和提高可靠性的关键技术。其中，齿廓修形可有效地缓和啮合齿数变化时引起的啮合刚度急剧变化，降低齿轮传动系统的振动[6]。文献[7-8]分别基于有限元模型和解析模型提出了定量计算修形齿轮啮合刚度的计算方法。Lin等[9]基于2自由度非线性动力学模型，研究了直线和抛物线修形对动载荷影响。文献[10-11]分别针对两级定轴齿轮传动系统和行星齿轮系统，采用不同动力学模型对比分析了齿廓修形对动态特性影响。王成等[12]建立了考虑齿轮运动状态和啮合状态的啮合刚度模型，研究了波动转矩作用下齿廓修形对动态特性影响。Marcello等[13]采用优化设计方法，对比研究了静态传递误差和动态传递误差最小时对应的齿廓修形参数。文献[14-15]将有限元法计算的啮合刚度代入动力学分析模型中，研究了含有不同修形量和修形长度齿轮的动态行为。杨玉良等[16]建立了具有12自由度的平行轴系斜齿轮转子系统动力学模型，研究了不同修形量对斜齿轮传动振动响应影响规律。王成等[17]和Liu等[18]建立了单级齿轮传动系统10自由度的横- 扭- 摆耦合非线性动力学模型，研究了齿廓修形对动载荷影响，并以减小齿轮传动系统的动载系数为目标开展了齿廓修形优化设计。综上所述，为提升高速重载车辆传动系统的功率密度，渐开线直齿轮普遍采用薄壁轮缘结构，而综合考虑薄壁轮缘结构和齿廓修形对啮合刚度影响，并开展齿轮动载荷研究的文献尚不多见。

本文考虑轮辐刚度、齿廓修形和齿轮实际运行状态，采用解析法计算啮合刚度，建立了齿轮啮合刚度模型。考虑几何偏心、陀螺力矩和齿向偏载力矩，建立了10自由度横- 扭- 摆耦合非线性动力学模型，并将啮合刚度模型和非线性动力学模型进行耦合计算。从定性和定量角度，对比分析了两种轮体结构齿轮动载荷随转速、扭矩、修形量和修形长度的变化趋势，所得结论可为齿轮减振和轻量化设计提供理论参考依据。

1 考虑轮辐刚度和齿廓修形的啮合刚度模型

1.1 齿廓修形齿轮啮合刚度模型

齿廓修形包括齿顶修形和齿根修形[6]，本文仅考虑齿顶修形(见图1)并将修形量表示为啮合线长度的函数。齿顶修形有多种类型，其中线性修形最常用，如(1)式所示：

(1)

式中：C为任意修形位置的修形量；s为任意修形位置的啮合线长度，s∈[sb,se]，sb和se分别为修形起始点和修形终止点对应的啮合线长度；Cmax为齿顶位置的最大修形量。

图1中，L为修形长度，rb为基圆半径。

啮合刚度随着啮合位置的变化而不断变化，表示为啮合点压力角的函数，结合单、双齿啮合和修形区动态边界条件，齿顶修形齿轮的啮合刚度计算分为5种情况[17-18]：1)啮合点在单齿啮合区内；2)啮合点在双齿啮合区内；3)啮合点在齿轮1修形区内；4)啮合点在齿轮2修形区内；5)啮合点同时在两个齿轮修形区内，其中，修形区的啮合刚度采用文献[7]方法计算。5种情况的啮合刚度分别为

(2)

(3)

(4)

(5)

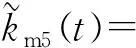
(6)

式中：αm(t)为啮合点压力角，是转速和中心距的时变函数[17]；ks(αm(t))为单对齿啮合刚度；ks1(αm(t))和ks2(αm(t))分别为双齿啮合时不同齿对的啮合刚度；Fm(t)为动态啮合力；C1(t)和C2(t)分别为齿轮1和齿轮2的修形量；中间变量E1(t)、E2(t)和E3(t)分别为

E1(t)=δ1(t)-C1(t)，

(7)

E2(t)=δ2(t)-C2(t)，

(8)

E3(t)=C1(t)-C2(t)，

(9)

δ1(t)=Fm(t)/ks1(αm(t))，

(10)

δ2(t)=Fm(t)/ks2(αm(t))，

(11)

δ1(t)和δ2(t)为双齿啮合时不同齿对的变形量。

采用解析法计算单对齿啮合刚度[6]：

(12)

式中：δBj(αm(t))为齿轮j轮齿本身的变形，采用Weber法并结合Cornell的判断条件计算；δC为轮齿之间的接触变形，采用赫兹接触模型计算；δMj(αm(t))为齿轮j轮体附加变形，本文考虑薄壁轮缘结构，采用1.2节解析方法计算。

1.2 薄壁轮缘齿轮轮体附加变形

将轮体分成3个部分，如图2所示。将每个部分看作内圈固定而外圈承受扭矩，则外圈相对于内圈将产生转角形变量，将3个部分的形变量叠加，可得轮体的总形变量。图2中：lr为轮缘处齿厚；lw为辐板处齿厚；lh为轮毂处齿厚；rh为第2部分圆孔中心与圆环中心的距离；dh为第2部分圆孔的直径；di1为轮毂内直径，do1为轮毂外直径；di2为轮缘内直径；do2为轮缘外直径。

1) 对于第1部分，设轮体承受扭矩为M，则任意横截面所受的扭矩为Mr=M/lr. 在截面半径为ρ处取宽度为dρ的微小圆环，其圆周位移为

(13)

式中：G为剪切模量。则圆环总的圆周位移为

(14)

2) 对于第2部分，无圆孔处的计算方法与第1部分相同。对圆孔部分，半径为ρ的微小圆环穿过其中的1个圆孔.ρ与rh之间的夹角为

(15)

设有n个圆孔，则圆孔外的圆环有效长度为

(16)

有效部分的圆环上所受剪应力τ=M/(ρlwL)，剪应变为

(18)

则宽度为dρ微小圆环的圆周位移为

(18)

穿过圆孔部分圆环的总圆周位移为

(19)

将无圆孔和有圆孔部分的圆周位移叠加，可得到第2部分的总圆周位移s2为

(20)

3)对于第3部分，将(14)式中的lr变为lh，且积分区间变为[di1/2,do1/2]，可得总圆周位移s3为

(21)

将3个部分相加可得到轮体总的圆周位移，再除以轮体半径，得到轮体转角为

θt=2(s1+s2+s3)/d1，

(22)

式中：s1、s2和s3分别为3个部分的圆周位移；d1为轮体直径。则薄壁轮缘齿轮的轮体附加变形为

δMi=θtRi，

(23)

式中：Ri为齿轮i的基圆半径。

1.3 啮合刚度有限元结果对比

采用有限元法计算单对齿啮合刚度并与本文解析法进行对比。齿轮副结构参数见表1，其中，方案1的轮体为实体，方案2的轮体为薄壁轮缘结构。

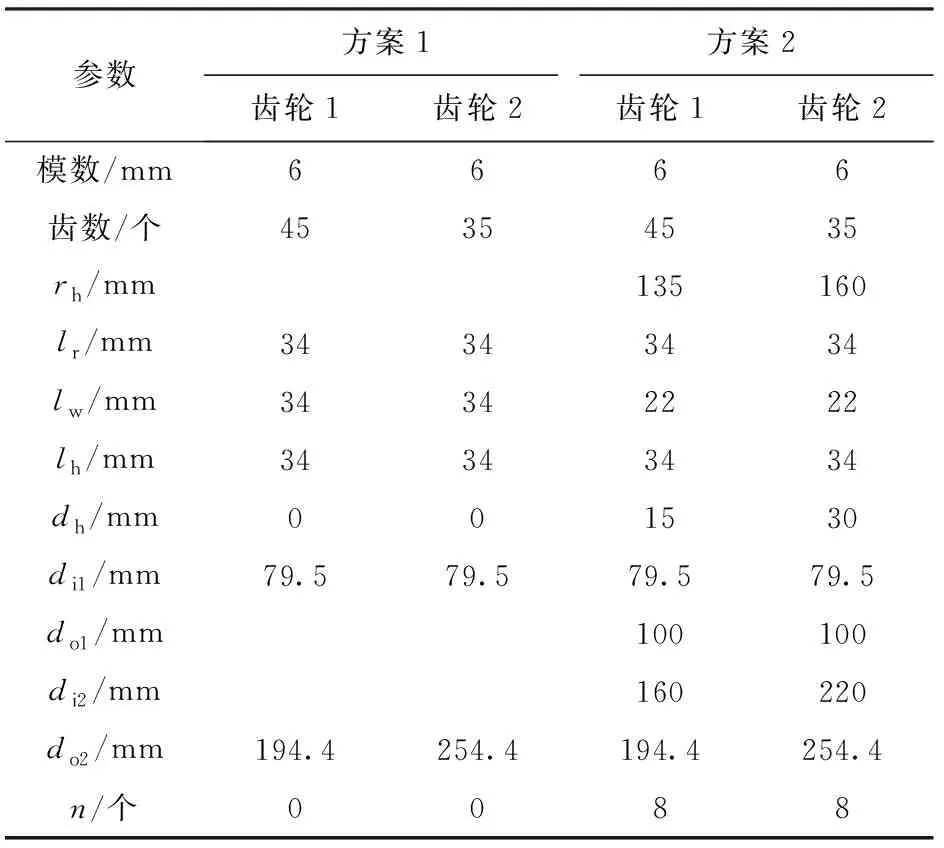
表1 齿轮副结构参数

不考虑接触变形，在齿轮内径施加固定约束，在两齿轮对应的啮合位置分别施加沿啮合线方向齿宽上均匀分布的载荷F，可得沿啮合线方向的变形量分别为δ1和δ2，则单对齿啮合刚度[19]为

(24)

式中：k1=F/δ1；k2=F/δ2.

薄壁轮缘齿轮1的三维有限元模型如图3所示。两种方案有限元计算结果和解析计算结果如图4所示。由表4可以看出，两种方法的计算结果吻合较好，最大误差小于6%，验证了薄壁轮缘齿轮啮合刚度计算模型的正确性。另外，方案2薄壁轮缘齿轮的啮合刚度较方案1实体齿轮的啮合刚度明显减小。

2 非线性动力学建模

针对图5所示的齿轮传动系统进行动力学建模，滚动轴承简化为弹性支撑，齿轮中心等效为传动轴和轴承的串联支撑；齿轮副通过沿着啮合面的作用力耦合在一起，啮合面始终与两齿轮的基圆相切。

齿轮传动三维动力学模型如图6所示，图6中有两种坐标系：第1种为各齿轮的局部坐标系oixiyizi，oi为传动轴理论中心位置；第2种为固定坐标系OXYZ，它与齿轮1的局部坐标系重合。A1A2B2B1为齿轮副间的啮合面。每个齿轮包含2个横向平移自由度xi和yi、1个扭转自由度θzi以及2个摆动自由度θxi和θyi. 图6中，Ci为质心，ei为偏心距，ψi为质心位置的初始转角。下标i=1代表齿轮1，i=2代表齿轮2.

考虑几何偏心、陀螺力矩和齿向偏载力矩，由拉格朗日方程可得单级齿轮传动系统的横- 扭- 摆耦合非线性动力学方程[17-18, 20-21]为

(25)

(26)

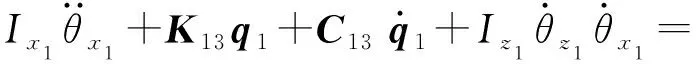
(27)

(28)

(29)

(30)

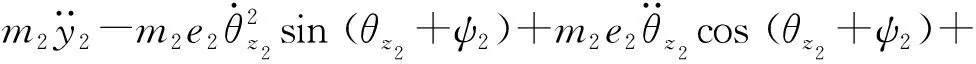
(31)

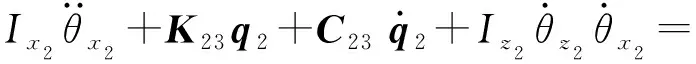
(32)

(33)

(34)

式中：kh为齿向偏载系数；α(t)和γ(t)分别为动态啮合角和位置角；mi为质量；Ixi、Iyi和Izi分别为转动惯量；Ti为外部激励；qi=[xi,yi,θxi,θyi,θzi]T；Kij和Cij分别为齿轮i中心支撑刚度矩阵和阻尼矩阵的第j行；下标i=1代表齿轮1，i=2代表齿轮2；下标j=1,2,3,4,5.

齿轮副通过沿啮合线方向上的啮合刚度、啮合阻尼和齿侧间隙耦合在一起，动态啮合力为

(35)

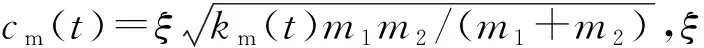
(36)

(37)

Δ(t)=(x1-x2)sin (α(t)+γ(t))-
(y1-y2)cos (α(t)+γ(t))+R1θz1-R2θz2+e(t)，

(38)

e(t)为齿廓修形引起的齿形偏差。

3 动载荷参数影响规律研究

针对表1所示齿轮副进行动载荷参数影响规律研究，动力学参数见表2，其中，单齿啮合最高点对应的修形长度为Lh=5.3 mm，当修形长度小于Lh为短修形，超过Lh为长修形。为描述齿轮动载荷随参数的变化规律，定义动载系数为

(39)

式中：Fmax为仿真时间内动态啮合力最大值；Fs为理论啮合力；Fm(t)为动态啮合力。

表2 齿轮动力学参数

3.1 两种轮体结构下转速扭矩对动载荷影响

不考虑齿廓修形，输入额定扭矩2 850 N·m，转速变化范围为[800 r/min, 2 300 r/min]，动载系数随转速的变化趋势如图7所示。由图7可见，随着转速增加，两种方案的动载系数均呈驼峰状变化，多数转速下薄壁轮缘齿轮的动载系数较大，最大增幅为6%. 方案1在转速为1 650 r/min时的动载系数最大为1.784，较转速为1 300 r/min时的最小动载系数1.458增加了22.3%；方案2在转速为1 650 r/min时的动载系数最大为1.835，较转速为1 350 r/min时的最小动载系数1.484增加了23.6%.

输入转速2 050 r/min，此时齿轮啮合刚度和动态啮合力分别如图8和图9所示。由图8和图9可见，两种方案在单、双齿啮合交替时均存在明显的刚度突变现象，且薄壁轮缘齿轮的单、双齿啮合刚度明显降低。薄壁轮缘齿轮的啮入冲击载荷增加，造成动载系数较大。由图10可知，两种方案的动态啮合力均以第2阶、第5阶和第6阶啮频对应幅值为主，其中，薄壁轮缘齿轮的动态啮合力2倍啮频和6倍啮频幅值明显增加。

不考虑齿廓修形，输入额定转速2 300 r/min，扭矩变化范围为[500 N·m,3 000 N·m]，动载系数随扭矩的变化趋势如图11所示。由图11可见：随着扭矩增加，动载系数总体均呈抛物线减小的趋势，但薄壁轮缘齿轮的动载系数在个别转速下存在局部峰值；两种方案的动载系数随转矩变化均不敏感，其中，方案1在扭矩为1 850 N·m时的动载系数最小为1.660，在扭矩为500 N·m时的动载系数最大为1.698；方案2在扭矩为1 850 N·m时的动载系数最小为1.649，在扭矩为700 N·m时的动载系数最大为1.690.

输入扭矩为3 000 N·m，此时动态啮合力时域曲线如图12所示。由图12可以看出，两种方案的啮入冲击载荷基本相同，动载系数差别较小。由图13可知，两种方案的动态啮合力均以2阶、4阶和5阶啮频对应幅值为主，其中，薄壁轮缘齿轮的动态啮合力2倍啮频对应的幅值明显减小。另外，薄壁轮缘齿轮5倍啮频幅值增加是出现局部峰值的主要原因。

3.2 两种轮体结构下齿廓修形对动载荷影响

两齿轮修形量和修形长度相同，其中，修形量取值范围为[0 mm, 0.1 mm]，取值间隔为0.001 mm，修形长度为2 mm. 在额定转速和扭矩工况下，动载系数随修形量变化如图14所示。由图14可以看出，随着修形量增加，动载荷系数均呈U形变化，即存在最优修形量使动载荷系数达到最小。当修形量超过最优值时，方案1的动载系数增加明显，而方案2的动载系数变化趋势缓慢。两种方案对应的最优修形量均为0.019 mm，对应的动载系数分别为1.376和1.385，分别较无修形齿轮的动载系数1.663和1.649减小了17.2%和16.0%. 两种方案对应的最优修形量均小于额定转矩作用下单齿啮合最高点的变形量。另外，存在临界修形量，当超过该值时齿轮动载系数大于无修形齿轮。两种方案对应的临界修形量分别为0.053 mm和0.073 mm. 在修形量为0.095 mm情况下，两种方案的动载系数差别最大，其中，方案1动载系数为2.365，较方案2的动载系数1.848增加了21.9%.

针对薄壁轮缘齿轮，进一步对比无修形和最优修形齿轮(修形量0.019 mm)的啮合刚度和动态啮合力时域曲线，分别如图15和图16所示。由图15、图16可以看出，齿廓修形有效地缓和了单、双齿啮合交替时啮合刚度的突变现象，同时齿廓修形有效地降低了啮入冲击载荷，动载系数明显降低。由图17所示的动态啮合力频域曲线可知，无修形齿轮的动态啮合力幅值以2倍啮频、4倍啮频和5倍啮频为主，而修形齿轮的动态啮合力幅值以1倍啮频、2倍啮频和5倍啮频为主。其中，修形齿轮1倍啮频的幅值显著增加，而2倍啮频、4倍啮频和5倍啮频的幅值明显降低。

两齿轮修形量和修形长度相同，其中，修形量为0.02 mm，修形长度的取值范围为[1.0 mm,6.0 mm]，取值间隔为0.1 mm. 在额定转速和扭矩工况下，动载系数随修形长度的变化趋势如图18所示。由图18可见，随着修形长度增加，两种轮体结构齿轮的动载荷系数变化趋势基本一致。当修形长度小于5.1 mm时，动载系数近似呈U形变化；当修形长度超过5.1 mm时，动载系数急剧减小。在修形长度为4.8 mm情况下，方案1的动载系数2.780较方案2的动载系数2.456增加了12.3%. 在短修形情况下，方案1和方案2对应的最优修形长度分别为2.5 mm和3.0 mm，对应的动载系数分别为1.335和1.352. 在长修形情况下，短修形和长修形对应的最优修形长度均为5.4 mm，对应的动载系数分别为1.060和1.128. 上述分析说明长修形可更有效地减低齿轮动载荷。

针对薄壁轮缘齿轮，进一步对比短修形3.0 mm和长修形5.4 mm的啮合刚度和动态啮合力时域曲线，结果分别如图19和图20所示。由图19和图20可知，长修形和短修形均有效地缓和了单、双齿啮合交替时啮合刚度的突变现象。由图20可知，长修形的动态啮合力波动小于短修形，动载荷明显降低。结合图19和图20，在修形区内，由于短修形动态啮合力的波动范围大，导致啮合刚度存在明显波动。由图21所示的动态啮合力频域曲线可知，短修形齿轮的动态啮合力幅值以1倍啮频、2倍啮频和4倍啮频为主，而长修形齿轮的动态啮合力幅值以2倍啮频、4倍啮频和5倍啮频为主。除5倍啮频外，长修形齿轮动态啮合力对应的幅值明显降低。

4 结论

本文考虑轮辐刚度、齿廓修形和齿轮实际运行状态，采用解析法计算啮合刚度，建立了齿轮啮合刚度模型，并与10自由度横- 扭- 摆耦合非线性动力学模型实现了耦合计算。所得主要结论如下：

1)随着转速增加，两种轮体结构齿轮的动载荷均呈驼峰状变化；多数转速下薄壁轮缘齿轮的动载荷较大，动态啮合力第2阶和第6阶啮频对应的幅值增加明显。

2)随着转矩增加，两种轮体结构齿轮的动载荷总体均呈抛物线减小，但薄壁轮缘齿轮在个别扭矩下存在局部峰值，动态啮合力在第2阶和第5阶啮频对应的幅值差别明显。

3)随着修形量增加，两种轮体结构齿轮的动载荷均呈U形变化，即存在最优修形量使动载荷达到最小，且最优修形量和最小动载系数基本相同；当修形量超过某临界值时，修形齿轮的动载荷大于无修形齿轮，且薄壁轮缘齿轮的临界修形量较大。

4)随着修形长度增加，短修形下动载荷均近似呈U形变化，长修形下动载荷急剧减小，说明长修形可更有效地降低齿轮振动。

参考文献(References)

[1] 刘辉, 蔡仲昌, 曹华夏, 等. 基于iSIGHT平台的车辆动力传动系统联轴器刚度优化研究[J]. 兵工学报, 2012, 33(2):228-231.

LIU Hui, CAI Zhong-chang, CAO Hua-xia, et al. The optimization study on the stiffness of coupling in vehicle powertrain based on iSIGHT platform[J]. Acta Armamentarii, 2012, 33(2):228-231.(in Chinese)

[2] 项昌乐, 何韡, 刘辉, 等. 履带车辆传动系统换挡工况瞬态动力学分析[J]. 农业机械学报, 2016, 47(4):288-293.

XIANG Chang-le, HE Wei, LIU Hui, et al. Transient dynamic analysis of tracked vehicle transmission during gear shift process[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4):288-293.(in Chinese)

[3] 刘辉, 项昌乐, 孙恬恬. 车辆动力传动系统弯扭耦合振动模型的建立及复模态分析[J]. 机械工程学报, 2010, 46(24):67-74.

LIU Hui, XIANG Chang-le, SUN Tian-tian. Construction of bending-torsional coupled vibration model and complex modal analysis of the vehicle powertrain[J]. Journal of Mechanical Engineering, 2010, 46(24):67-74.(in Chinese)

[4] Liu H, Wang C, Xiang C L. Dynamic characteristic optimization of vehicle transmission based on lateral-torsional coupled nonlinear dynamic model[C]∥Proceedings of the 6th International Conference on Modelling, Identification & Control. Melbourne, Australia:IEEE, 2014: 149-154.

[5] 刘辉, 蔡仲昌, 朱丽君, 等. 多挡条件下单级行星传动非线性振动特性研究[J]. 兵工学报, 2012, 33(10):1153-1161.

LIU Hui, CAI Zhong-chang, ZHU Li-jun, et al. Study on nonli-near vibration behavior of simple single stage planetary gears in multiple work conditions[J]. Acta Armamentarii, 2012, 33(10):1153-1161. (in Chinese)

[6] 李润方. 齿轮传动的刚度分析和修形方法[M]. 重庆:重庆大学出版社, 1998.

LI Run-fang. Mesh stiffness analysis and modification method of gear transmission[M]. Chongqing: Chongqing University Press, 1998. (in Chinese)

[7] Chen Z G, Shao Y M. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62: 63-74.

[8] 唐进元, 蔡卫星, 王志伟. 修形圆柱齿轮啮合刚度计算公式[J]. 中南大学学报:自然科学版, 2017, 48(2):337-342.

TANG Jin-yuan, CAI Wei-xin, WANG Zhi-wei. Meshing stiffness formula of modification gear[J]. Journal of Central South University: Science and Technology, 2017, 48(2):337-342. (in Chinese)

[9] Lin H H, Oswald F B, Townsend D P. Dynamic loading of spur gears with linear or parabolic tooth profile modifications[J]. Mechanism and Machine Theory, 1994, 29:1113-1129.

[10] Liu G, Parker R G. Dynamic modeling and analysis of tooth profile modification for multimesh gear vibration[J]. Journal of Mechanical Design, 2008, 130(12): 121402-1-121402-12.

[11] Bahk C J, Parker R G. Analytical investigation of tooth profile modification effects on planetary gear dynamics[J]. Mechanism and Machine Theory, 2013, 70:298-319.

[12] 王成, 刘辉, 项昌乐. 波动扭矩下渐开线直齿轮传动齿廓修形研究[J].振动与冲击, 2014, 33(24):32-38, 53.

WANG Cheng, LIU Hui, XIANG Chang-le. Influences of profile modification on dynamic characteristics of involute spur gears under a fluctuating torque[J]. Journal of Vibration and Shock, 2014, 33(24):32-38, 53. (in Chinese)

[13] Marcello F, Farhad S, Gabrieie B, et al. Dynamic optimization of spur gears[J]. Mechanism and Machine Theory, 2011, 46: 544-557.

[14] 陈思雨, 唐进元, 王志伟, 等. 修形对齿轮系统动力学特性的影响规律[J]. 机械工程学报, 2014, 50(7):39-45.

CHEN Si-yu, TANG Jin-yuan, WANG Zhi-wei, et al. Effect of modification on dynamic characteristics of gear[J]. Journal of Mechanical Engineering, 2014, 50(7):39-45.(in Chinese)

[15] 马辉, 逄旭, 宋溶泽, 等.考虑齿顶修缘的齿轮- 转子系统振动响应分析[J]. 机械工程学报, 2014,50(7)：39-45.

MA Hui, PANG Xu, SONG Rong-ze, et al. Vibration response analysis of a geared rotor system considering the tip relief[J]. Journal of Mechanical Engineering, 2014, 50(7):39-45.(in Chinese)

[16] 杨玉良, 魏静, 赖育彬, 等. 考虑齿顶修缘的斜齿轮传动振动响应分析[J]. 重庆大学学报, 2017, 40(1):31-40.

YANG Yu-liang, WEI Jing, LAI Yu-bin, et al. Vibration response analysis of helical gear transmission considering the tip relief[J]. Journal of Chongqing University, 2017, 40(1):31-40.(in Chinese)

[17] 王成, 刘辉, 项昌乐. 基于齿轮传动系统横- 扭- 摆耦合非线性动力学模型的齿廓修形优化设计[J]. 振动与冲击, 2016, 35(1): 142-148.

WANG Cheng, LIU Hui, XIANG Chang-le. Optimal profile modification for spur gear systems based on their lateral-torsional-rocking coupled nonlinear dynamic model[J]. Journal of Vibration and Shock, 2016, 35(1): 142-148.(in Chinese)

[18] Liu H, Zhang C, Xiang C L, et al. Tooth profile modification based on lateral-torsional-rocking coupled nonlinear dynamic model of gear system[J]. Mechanism and Machine Theory, 2016, 105: 606-619.

[19] Chaari F, Fakhfakh T, Haddar M. Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness[J]. European Journal of Mechanics A/Solids, 2009, 28(3):461-468.

[20] 刘辉, 张晨, 王成. 两级渐开线齿轮传动系统横- 摆- 扭耦合非线性动力学建模与试验验证[J]. 振动与冲击, 2017, 36(15):124-132.

LIU Hui, ZHANG Chen, WANG Cheng. Nonlinear dynamic modeling and test validation for a two-stage involute gear system[J]. Journal of Vibration and Shock, 2017, 36(15): 124-132. (in Chinese)

[21] 王成. 渐开线直齿轮传动系统非线性动力学研究[D].北京： 北京理工大学, 2015.

WANG Cheng.Nonlinear dynamic research of involute spur gear system [D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese)