水下航行器环肋复合材料耐压壳6σ优化设计

李彬， 庞永杰， 朱枭猛， 程妍雪

(1.哈尔滨工程大学 水下机器人技术重点实验室， 黑龙江 哈尔滨 150001;2.哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001)

0 引言

作为水下航行器的主要结构之一，耐压壳不但能够为载体提供浮力储备，而且是各分类系统设备正常工作的重要保证。特别是环肋圆柱壳具有利于内部舱室布置、加工简单等特点，在水下航行器结构中应用广泛[1]。复合材料作为新型材料的代表，具有比强度大、比刚度高、耐腐蚀性好、结构可设计等特点，与传统金属耐压壳结构相比，在相等强度、刚度条件下，质量大幅度减轻，对增加水下航行器有效载荷、提高续航力有重要意义[2-3]。普通金属耐压壳通常采用外部环肋结构形式来提高耐压壳的整体稳定性[4]。对于复合材料耐压壳结构而言，采用外部加环肋方式不利于加工；采用无肋骨方式需要增加单层厚度，使成本提高、影响经济性能；而采用内部加环肋形式则既可以避免外部环肋和无肋骨方式的不利情况，又可以起到加强结构作用[5]。

应用基于确定性的传统分析方法对环肋复合材料耐压壳结构进行设计时，通常视各变量为确定值，并忽略变量随机分布对结果造成的影响。复合材料各向异性的特点使其对几何尺寸等随机因素变化非常敏感。由于复合材料具有不均匀特性，以至于结构性能对复合工艺的依赖性较强，而各环节工艺参数很难准确把控，致使其偏离确定性分析得到的结果[6]。因此，为保证结构安全性，对环肋复合材料耐压壳结构进行可靠性分析是十分必要的。宋云连等[7]采用随机有限元法对复合材料层合板可靠性分析进行了研究。羊姈等[8]提出了用于复合材料结构可靠性优化的多级优化技术。陈建桥等[9]对粒子群优化算法进行了改进，并应用于复合材料结构可靠性优化中，解决了实际工程中非线性、多极值、不易收敛等问题。

耐压壳可靠性分析结果表明，确定性设计方法虽然能对结构性能优化进行定量计算，但得到的结果具有局限性，无法准确预测可靠性和结构失效分散性[10]。因此，需要一种综合考虑结构性能优化、可靠的方法来指导环肋复合材料耐压壳设计[11]。6σ设计方法作为一种统计优化方法，可对设计参数进行最佳组合，降低各种设计制造所带来的风险，获得满足各方面要求的高质量产品。其中σ是表示产品性能参数标准方差的统计学术语，σ水平用来衡量产品性能约束偏离其平均值的程度。假设产品性能约束波动呈正态分布，约束上下限内面积越大，可靠性越高，其相应的σ水平就越高[12]。然而，6σ设计寻优过程迭代次数过多，导致计算成本非常大，为避免在优化过程中出现数值噪声和错误，可以引入径向基函数(RBF)神经网络近似模型技术代替庞大的仿真计算，以期在保证精度的同时大幅度节约计算成本。

本文基于以上思想，结合6σ设计理论，应用蒙特卡洛抽样模拟方法对某水下航行器环肋复合材料耐压壳结构进行可靠性分析，以耐压壳质量最小为优化目标，借助RBF神经网络近似模型技术，以σ水平为可靠度评价指标，提出了考虑可靠性的环肋复合材料耐压壳结构优化设计框架，以实现兼顾结构质量和稳健性的高效率最优方案。

1 复合材料耐压壳确定性优化方案

优化目标为某潜深2 000 m的水下航行器环肋复合材料耐压壳，耐压壳结构采用金属内衬外部缠绕纤维增强复合材料的形式，肋骨采用内部环肋布置方式，结构长度L为1 000 mm，内半径R为150 mm，4根肋骨左右对称布置，肋骨宽为b，肋骨高为h，金属内衬材料选用7075铝合金，复合材料采用环氧树脂作为基体，T800碳纤维作为增强纤维，为避免拉伸- 弯曲耦合影响采用12层对称铺设，铺设角度为[0°,45°,90°,-45°,45°,90°]sym，各单层材料性质相同，材料性能参数如表1所示，耐压壳剖面如图1所示。

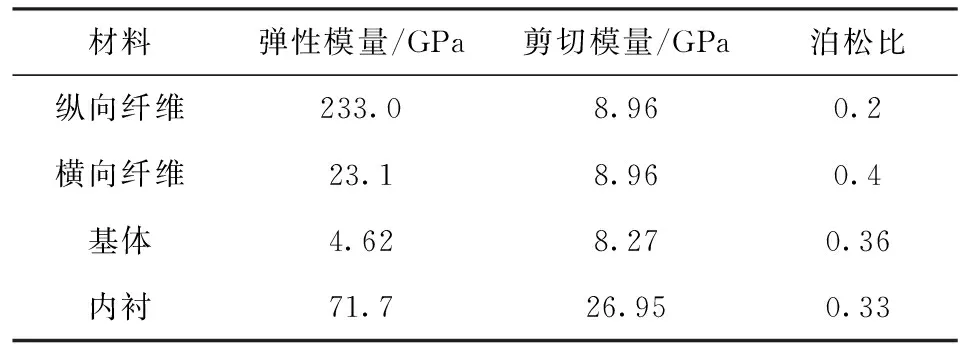
表1 材料力学性能参数

选取复合材料纤维体积分数为Vf，层合板厚为t，b和h作为优化参数，参数取值范围如下：0.3≤Vf≤0.8, 12 mm≤t≤18 mm,15 mm≤b≤30 mm,15 mm≤h≤30 mm，根据《潜水系统和潜水器入级与建造规范》[13]，承受外压的环肋耐压壳需保证壳体相邻肋骨中点处壳板的周向应力σ1、肋骨处壳板轴向应力σ2和肋骨应力σr均小于铝合金材料肋骨屈服强度σs，其中σs=455 MPa. 除了结构强度之外，对于受外压的薄壳结构而言，稳定性也是结构分析需要重点考虑的因素之一。本文耐压壳设计潜深为2 000 m，安全系数取1.5，设计压力pd为30 MPa，当临界失稳压力pcr大于设计压力pd时认为结构满足稳定性要求[14]。另外，由于复合材料具有各向异性的特点，使其失效准则与金属材料不同。本文采用Tsai-Wu张量理论[15]作为判定复合材料层失效的依据。用以下(1)式、求解平面应力下正交各向异性复合材料的失效指数Fc，其中，Fi和Fij为张量项系数(i、j表示6个自由度，i，j=1，2，…，6)，当失效指数Fc小于1时认为结构满足强度要求。

(1)

优化问题定义如下：

minm(Vf,t,b,h)，
s.t.σ1≤0.85σs，σ2≤1.15σs，σr≤0.6σs，pcr≥pd，Fc<1,tmin≤t≤tmax，Vf，min≤Vf≤Vf，max，bmin≤b≤bmax，hmin≤h≤hmax.

(2)

本文优化过程不考虑随机因素变化对结果的影响，单纯在设计空间中搜索满足强度和稳定性约束的质量最轻解，因此可得到环肋复合材料耐压壳的确定性优化结果：纤维体积分数Vf=0.78，层合板厚t=0.015 mm，肋骨宽b=0.028 mm，肋骨高h=0.016 mm. 对应的相邻肋骨中点壳板周向应力σ1=226.62 MPa，肋骨处壳板轴向应力σ2=99.62 MPa，肋骨应力σr=249.65 MPa，失效指数Fc=0.84，临界失稳压力pcr=64.72 MPa，耐压壳整体质量m=32.76 kg.

2 基于蒙特卡洛模拟的耐压壳可靠性分析

对于有约束的优化问题，优化目标和约束条件往往相互矛盾，最优解通常收敛于约束边界。这意味着偏离最优解就有可能跃出约束边界，从而对实际加工过程的精度控制提出了更高要求。然而复合材料壳体各尺寸加工精度难以控制，且材料属性也会根据环境等原因偏离名义值，使加工产品结构参数偏离最优解，从而对结构响应产生影响，结构失效的可能性将因此增加。由上文环肋复合材料耐压壳结构确定性优化结果可以看出，肋骨应力和失效指数与约束边界已非常接近，结构性能将面临上述问题，因此可靠性分析将具有重要意义。本文采用有限元方法与蒙特卡洛抽样方法相结合方式对耐压壳结构进行可靠性分析。假设纤维体积分数、层合板厚和肋骨尺寸为随机变量，变量之间相互独立且服从正态分布，响应值为相邻肋骨中点壳板周向应力、肋骨处壳板轴向应力、肋骨应力、失效指数和临界失稳压力。为保证在较少抽样次数的同时得到较高可信度响应，应用描述性抽样方法对1 000组响应值进行统计分析，考察最优解在不确定性环境下的稳健性。由表2所示的可靠性分析结果可以看出，输出响应的统计平均值和最优解都存在一定差异，其中，复合材料失效指数可靠度为92.6%，肋骨强度可靠度为82.6%. 显然，在考虑材料分散性和加工不确定性之后，确定性优化方案存在失效的可能。

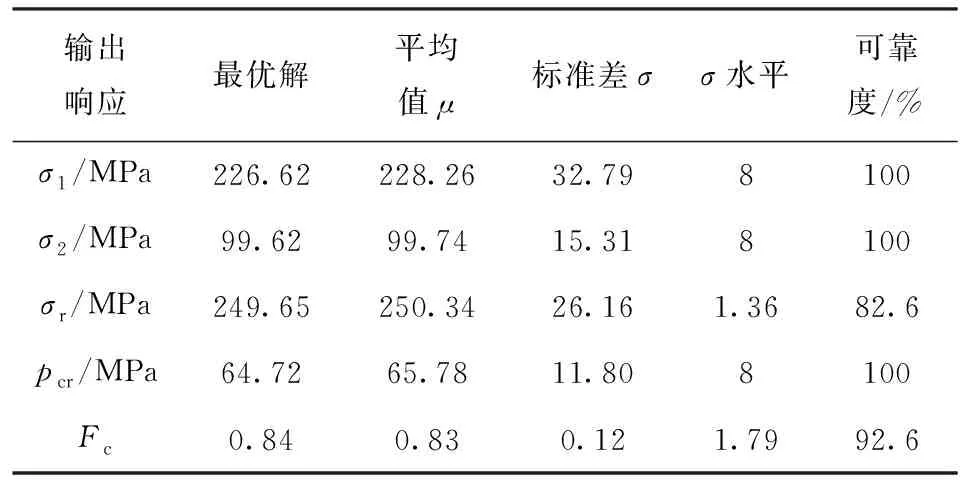
表2 可靠性分析结果

3 复合材料耐压壳6σ优化设计

3.1 优化问题定义

依据蒙特卡洛抽样方法统计可靠度分析结果，目标为最小化质量，相邻肋骨中点壳板周向应力、肋骨处壳板轴向应力、肋骨应力、失效指数和临界失稳压力在其均值6倍标准差范围内满足性能要求。环肋复合材料耐压壳6σ优化问题定义如下：

minm(Vf,t,b,h)，
s.t.σ1±6σσ1≤387 MPa,σ2±6σσ2≤523 MPa,σr±6σσr≤273 MPa,pcr±6σpcr≥30 MPa,Fc±6σFc<1,12 mm≤t≤18 mm,0.3≤Vf≤0.8,15 mm≤b≤30 mm,15 mm≤h≤30 mm,

(3)

式中：6σσ1、6σσ2、6σσr、6σpcr和6σFc分别表示相邻肋骨中点壳板周向应力σ1、肋骨处壳板轴向应力σ2、肋骨应力σr、失效指数Fc以及临界失稳压力pcr的6倍标准差。

3.2 RBF神经网络近似模型

传统的结构优化方法往往需要将不同参数组合成多个方案，通过反复迭代来研究各因子对结构性能影响。由于环肋复合材料耐压壳结构的复杂性和更多的设计参数，使得优化设计研究工作量加大，采用有限元仿真技术时，随着模型复杂程度的增大及对计算精度要求的提高，进行一次迭代需要花费较长时间，使设计周期和设计成本随之增加，而近似模型技术能够较好地解决复杂系统分析计算代价高昂问题。近似模型技术是通过有限次仿真计算来构建一个计算消耗小但精度足够的代理模型，通过数学模型代替高成本的仿真分析。目前，对于耐压壳结构研究常用的近似模型主要是RBF模型，它是由输入层、隐含层和输出层构成的前馈型网络模型，其基本思想是以待测点与样本点间的欧几里得距离为自变量，对于N维输入变量x1,…,xN∈R，以径向函数gi=g(‖x-xj‖a)∈R(其中0.2≤a≤3.0，xj表示RBF的中心，j=1,…,N)为基函数，通过线性叠加方式构造RBF模型[16]。对于任意输入变量x，设第j个径向基神经元对应的输出函数为

(4)

式中：σf为函数的平坦度；cj为第j个基函数的中心。σf越大，以cj为中心的等高线越稀松。

采用近似模型技术，用有限次仿真结果构建代理模型来求解环肋复合材料耐压壳6σ优化问题，在构建近似模型时将纤维体积分数Vf、层合板厚度t、肋骨宽b和肋骨高h作为输入参数。为保证优化的精确性，需要近似模型空间大于优化设计空间。将相邻肋骨中点壳板周向应力σ1、肋骨处壳板轴向应力σ2、肋骨应力σr、临界失稳压力pcr以及失效指数Fc作为输出参数，采用拉丁超立方设计方法安排1 000次实验设计，依据参数样本响应值构建RBF神经网络近似模型。图2为保持其他参数固定时Vf和t与输出响应Fc和pcr的近似模型三维图。由图2可知，失效指数Fc随着Vf和t的减小而增大，临界失稳压力pcr随着Vf和t的增大而增大。

3.3 误差分析

复相关系数R2用来评估近似模型估计值与响应真实值之间的相符程度，R2值由以下(5)式定义：

(5)

式中：n为样本点数；yi为响应实际值；i为模型估计值；为真实值的平均值；R2越接近1表示模型精度越高。通常认为在样本点足够多的情况下，R2值在0.9以上时近似模型与实际值就足够逼近。为衡量样本模型与样本点的吻合程度，在设计空间内随机选取200个样本点进行误差分析。通过计算复相关系数可以得到所有输出响应的R2值均在99%以上。以临界失稳压力和失效指数为例展示近似模型与仿真计算对比，结果如图3所示。由图3可以直观地看出，各点均以极小误差落在直线y=x上，说明近似模型预测值与仿真计算值的重合度非常高，模型精度满足要求。因此，基于RBF近似模型的优化分析方法，能以少量仿真计算结果拟合出反映整个设计空间属性的近似分析模型，代替实际仿真计算参与6σ优化设计，在保证准确的同时在很大程度上减少目标函数和约束函数评估的计算量，从而提高设计进程和分析效率。

3.4 优化结果

借助RBF神经网络近似模型，应用多岛遗传算法对环肋复合材料耐压壳结构进行6σ优化设计，得到以下结果：

1) 环肋复合材料耐压壳设计变量最优解为Vf=0.53,t=0.017 mm,b=0.028 mm,h=0.028 mm，输出响应σ1=277.33 MPa,σ2=139.94 MPa，σr=228.18 MPa,Fc=0.61,pcr=110.84 MPa，耐压壳质量m=35.87 kg.

2) 各响应概率分布如图4所示，图4中标注了各性能指标的均值、标准差及σ水平。由图4可见，经过优化后，相邻肋骨中点壳板周向应力σ1、肋骨处壳板轴向应力σ2、肋骨应力σr、临界失稳压力pcr和失效指数Fc5项结构性能约束都达到了8σ水平，结构具有较高的可靠度。

3) 确定性优化与6σ优化设计结果如表3所示。由表3可知，6σ优化结构质量相比确定性优化结果增加了3.11 kg，但设计变量Vf在确定性优化中偏高且接近边界。由此可见，过高的纤维体积分数Vf在实际生产中难以实现，常会引入未知误差，对结构质量及性能产生影响。

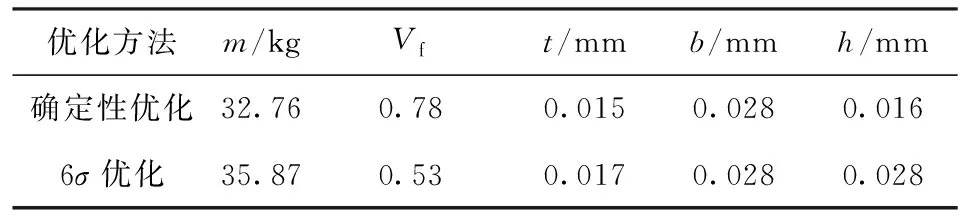
表3 优化结果对比

4) 相邻肋骨中点壳板周向应力σ1、肋骨处壳板轴向应力σ2、肋骨应力σr、临界失稳压力pcr以及失效指数Fc等结构性能约束对比如表4所示。由表4可以看出，在纤维体积分数、层合板厚度和肋骨尺寸服从正态分布情况下，确定性优化中肋骨应力σr和失效指数Fc的可靠度较低，且输出响应的统计平均值和最优解都存在一定差异，结构可能会由于随机参数变化而失效。相比确定性优化，6σ优化方案虽然增加了3.11 kg质量，但耐压壳结构性能约束的σ水平提高到了8σ以上，可靠度达到100%.

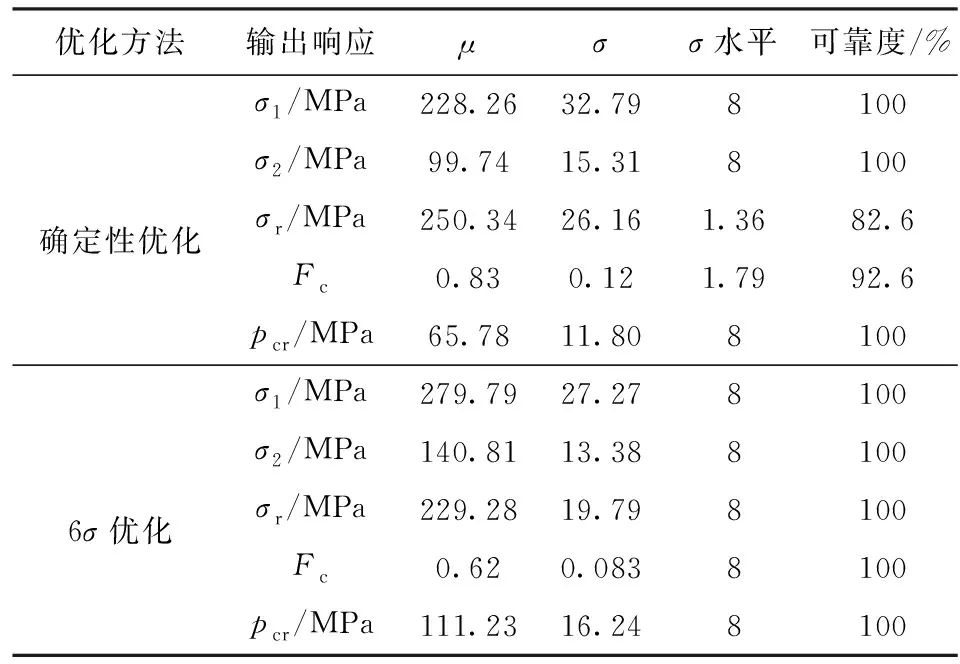
表4 输出响应对比

4 结论

本文将6σ设计理论引入水下航行器环肋复合材料耐压壳优化设计中，应用蒙特卡洛抽样模拟方法对耐压壳结构进行可靠性分析，借助RBF神经网络近似模型技术，以σ水平为评价指标对环肋复合材料耐压壳结构进行考虑可靠性的优化设计，结果表明：

1) 在确定性优化中设计变量纤维体积分数的最优解偏高且接近边界。过高的纤维体积分数在实际生产中难以实现，常会引入未知误差，对结构质量及性能产生影响。

2) 对于肋骨应力及失效指数两项结构性能约束，确定性优化方法得到的可靠度较低，使得结构存在由于随机参数变化而失效的可能。

3) 6σ优化设计方法虽然使结构质量增加了3.11 kg，却使耐压壳结构性能约束的σ水平全部达到了8σ水平，可靠度达到100%.

4) 本文所提出的基于RBF神经网络近似模型的6σ优化设计与可靠性评估相结合优化方法，综合考虑了目标优化和性能约束的可靠度，避免随机参数波动可能带来的结构失效，可以准确、高效、可靠地对水下航行器环肋复合材料耐压壳进行优化，亦可作为理想的结构可靠性优化方法推广到复合材料水下航行器载体结构整体设计中。

参考文献(References)

[1] Shang G F, Zhang A F, Wang Z Q. Optimum design of cylindrical shells under external hydrostatic pressure[J]. Journal of Ship Mechanics, 2010, 14(12): 1384-1393.

[2] Lee G C, Kweon J H, Choi J H. Optimization of composite sandwich cylinders for underwater vehicle application[J]. Composite Structures, 2013, 96(4):691-697.

[3] Davies P, Choqueuse D, Bigourdan B, et al. Composite cylinders for deep sea applications: an overview[J]. Journal of Pressure Vessel Technology, 2016, 138(6): 060904.

[4] Li B, Pang Y J, Cheng Y X, et al. Collaborative optimization for ring-stiffened composite pressure hull of underwater vehicle based on lamination parameters[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(4): 373-381.

[5] 李彬, 庞永杰, 程妍雪，等. 基于EBF神经网络的复合材料耐压壳性能研究[J].哈尔滨工程大学学报，2016,37(10): 1323-1329.

LI Bin, PANG Yong-jie, CHENG Yan-xue, et al. Research on a composite pressure hull based on an EBF neural network[J]. Journal of Harbin Engineering University，2016,37(10): 1323-1329.(in Chinese)

[6] Moses F. System reliability developments in structural engineering[J]. Structural Safety, 1982, 1(1): 3-13.

[7] 宋云连, 李树军, 王善. 加强纤维复合材料板结构的可靠性分析[J].哈尔滨工程大学学报，1999,20(3): 63-71.

SONG Yun-lian, LI Shu-jun，WANG Shan. The reliability analysis for the fiber-reinforced composite plate[J]. Journal of Harbin Engineering University，1999, 20(3): 63-71.(in Chinese)

[8] 羊姈, 马祖康, 庄力舟. 采用多级优化技术进行复合材料结构可靠性优化设计[J]. 航空学报, 1993, 14(8): 408-411.

YANG Ling, MA Zu-kang, ZHUANG Li-zhou. Optimum design of reliability for composite structure using multi-level optimization technique[J]. Acta Aeronautica et Astronautica Sinica, 1993, 14(8): 408-411.(in Chinese)

[9] 陈建桥, 魏俊红. 基于粒子群算法的复合材料可靠性优化设计[J].华中科技大学学报, 2006, 34(4): 96-98.

CHEN Jian-qiao, WEI Jun-hong. Reliability optimal design of composite materials based on the particle swarm optimization algorithm [J]. Journal of Huazhong University of Science and Technology, 2006, 34(4): 96-98.(in Chinese)

[10] Chen J Q, Ge R, Wei J H. Probabilistic optimal design of laminates by using the improved particle swarm optimization[J].Engineering Optimization, 2008, 40(8): 695-708.

[11] Rackwitz R, Flessler B. Structural reliability under combined random load sequences[J]. Computers & Structures, 1978, 9(5): 489-494.

[12] 程妍雪, 庞永杰, 冯亮. 基于径向基神经网络模型的耐压壳6σ设计[J]. 上海交通大学学报, 2014, 48(4): 493-497.

CHENG Yan-xue, PANG Yong-jie, FENG Liang. 6σdesign for pressurized cylindrical shells based on RBF[J]. Journal of Shanghai Jiao Tong University, 2014, 48(4): 493-497. (in Chinese)

[13] 中国船级社. 潜水系统和潜水器入级与建造规范[S]. 北京: 人民交通出版社, 1996.

China Classification Society. Specification for entry and construction of diving systems and submersibles [S].Beijing: China Communications Press, 1996. (in Chinese)

[14] 李彬, 庞永杰, 程妍雪，等.协同优化基于铺层参数的复合材料耐压壳协同优化设计[J]. 上海交通大学学报, 2017, 51(7): 208-213.

LI Bin, PANG Yong-jie, CHENG Yan-xue, et al. Collaborative optimization for composite material pressure hull based on lamination parameter[J]. Journal of Shanghai Jiao Tong University, 2017, 51(7): 208-213. (in Chinese)

[15] Jones R M. Mechanics of composite materials [M].2nd ed. Oxford，UK: Taylor & Francis Group, 1999.

[16] 杨卓懿. 无人潜器总体方案设计的多学科优化方法研究[D]. 哈尔滨:哈尔滨工程大学, 2012.

YANG Zhuo-yi. A study on multidisciplinary design optimization method for scheme design of autonomous underwater vehicle[D].Harbin:Harbin Engineering University, 2012. (in Chinese)